分位数自回归变点模型的贝叶斯分析及应用

郭 婧，何幼桦

（上海大学 理学院，上海 200444）

0 引言

传统的线性回归模型是对响应变量的条件均值进行建模，它描述了解释变量在均值上对响应变量的影响。用普通最小二乘方法对回归参数进行统计分析要求模型的误差项的分布具有正态假设。但很多实际经济金融数据常常并不满足这些假设，例如数据出现尖峰或厚尾的分布，存在显著的异方差性以及不对称性等。此时的最小二乘法估计将不再具有稳健性。为了能够更好地刻画解释变量在分布各个位置上对被解释变量的影响，以及在数据不满足均值回归的假设时提高估计的稳健性，Koenker和Bassett（1978）[1]提出了分位数回归的思想。他们在模型中将响应变量的条件分位数表示为协变量的线性函数，通过最小化样本的绝对残差的非对称函数，得到随机变量y的条件分位数的估计。类似于一般的线性模型，分位数回归模型对误差项的分布也有相应的假设：对于固定的分位数，误差项的条件分位数为零。

在分位数模型的基础上，R.Koenker和Z.Xiao（2006）[2]提出了分位数自回归模型，给出了模型的估计方法,以及在不同分位数上的平稳性检验统计量。Hideo Kozumi和Genya Kobayashi（2011）[3]最先给出了分位数回归有效的Gibbs抽样方法。而在实际应用方面,陈耀辉等（2015）[4]使用分位数回归基本思想,引入自回归分布滞后效应，借助非对称Laplace分布进行贝叶斯估计，构建基于Gibbs抽样的贝叶斯自回归分布滞后分位数回归模型。之前学者对各类分位数模型的研究表明，使用贝叶斯方法可以很好地解决该类模型复杂的参数估计问题。

近二十年来,关于变点问题研究在理论和应用等方面都有了快速的发展。LY Vostrikova（1981）[5]提出的二分分段法能够同时检测出变点的数量和位置，并能够节省计算时间。陈希孺（1988）[6]利用局部法，研究了变点的检验问题；1991年又对变点问题的研究进行了综述[7-10]。

近年来对于变点问题的贝叶斯方法研究，都是基于对联合概率密度求积分而得到各个参数的边际后验。但是当模型比较复杂，或者对于分布假设更加一般的情况下，对联合概率密度求积分的方法就不可行了。本文将研究分位数自回归变点模型贝叶斯分析方法，由于假设分布的复杂性，拟采用MCMC抽样方法得到参数的后验分布。

1 模型

Koenker和Xiao（2006）[2]提出可以将分位数自回归模型当作特殊的随机系数自回归模型，考虑模型：

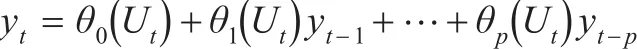
如果等式右边的函数都关于随机变量Ut单调递增，具有函数依赖关系,并设随机变量Ut～U（0，1），则上式可以写为：

为解决滞后项之间的共线性问题，陈耀辉等（2015）[4]使用ADF检验的模型形式：

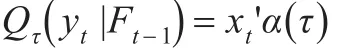
考虑有变点的分位数自回归模型。假设序列在时刻k滞后项的回归系数发生了突变，模型表示为：

设yt服从非对称的拉普拉斯分布：

f（x;μ，σ，τ）=στ exp（- σρ（x- μ））

记为 x～ALD（μ，σ，τ）,其中0＜ τ＜1是偏度参数,σ＞0是尺度参数,-∞＜μ＜∞ 是位置参数,函数 ρτ（u）=u（τ-I（u≤0））。可以证明,如果随机变量 x 服从 ALD（μ，σ.τ）,则有即位置参数μ就是分布的τ分位数。所以在序列yt服从ALD的假设下,估计模型的参数与求序列的τ分位数是等价的。

在序列存在变点的假设下,使用非对称的拉普拉斯分布

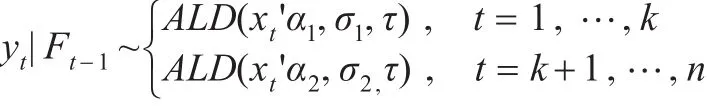
2 贝叶斯分析

为了得到更容易抽样的后验分布,Tsionas（2003）[11]对非对称的拉普拉斯分布进行了研究。如果一个随机变量服从三参数的拉普拉斯分布,x～ALD（μ，σ，p）,那么 x可以等价表示成

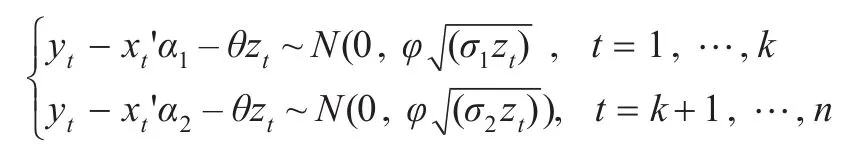
得到给定参数下样本的联合密度函数：

所以参数的联密度函数：

根据上述得到的参数联合后验密度函数,结合文献[4]和文献[11]的计算结果,通过推导计算可以得到变点分位数模型各参数的后验核密度函数。

2.1 回归系数 α1（α2）

假设先验，α1～N（α10，Σ10），得到其后验：

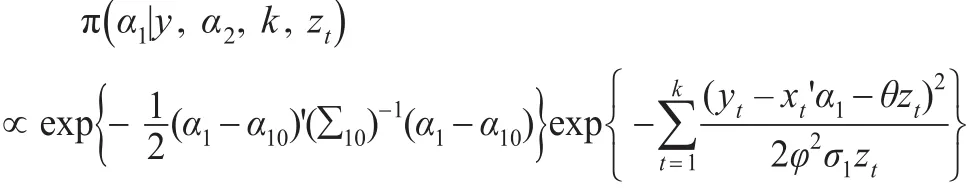
α2有类似的结论。

2.2 尺度参数参数 σ1（σ2）

由于 zt|σ ～E（1 σ）,σ1的后验:

π（σ1|y， α1， α2， k， zt）

即σ1服从逆伽马分布有类似的结论。

2.3 参数zt

设zt的先验分布为参数λ=1的指数分布,得到后验:

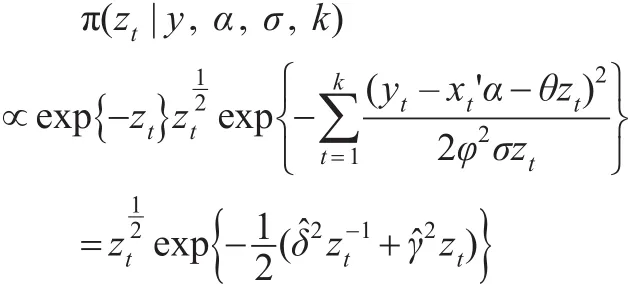
其中:

即zt从广义逆高斯分布

2.4 变点时刻k

假设k先验密度为π（k）,则其后验分布:

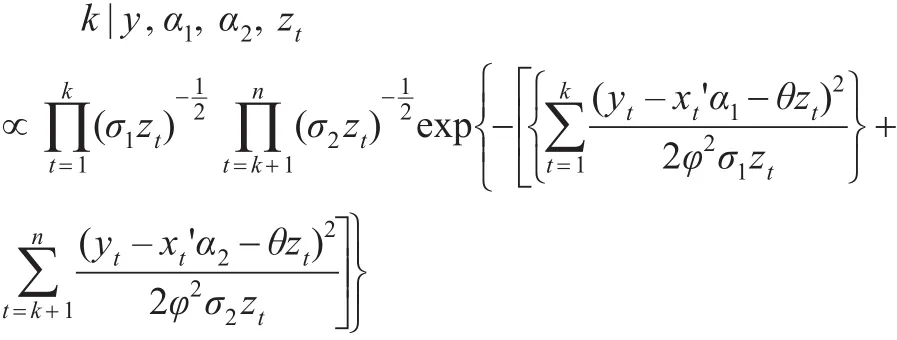
由于k的后验核密度函数较复杂,所以在MCMC抽样中k的抽取使用M-H方法。在各参数的满条件分布的基础上,给出了MCMC抽样算法。

（6）计算接受概率

（7）从均匀分布 U（0，1）中抽取 ui,如果 ui＜a（k（*），k（i-1）），接受 k（*），记 k（i）=k（*）；否则，拒绝 k（*），记 k（i）=

（8）重复步骤（2）到步骤（7），直到完成设定的抽样次数。

3 仿真模拟

3.1 仿真数据

为了验证上述MCMC抽样方法的有效性,在实证研究之前先进行仿真实验。仿真数据根据模型产生：

其中,Ut～U（0，1）,滞后项阶数为2,记样本量为 n,每次抽样变点时刻k设为n 2。模型变点前后仅滞后项系数之和 α1变化,变点前各个分位数上| α1（τ）|的值都小于1。而在变点之后,高分位数上| α1（τ）|接近甚至超过1。本文使用无信息先验,选取τ=0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,共9个分位数进行抽样。

3.2 抽样结果

在抽样过程中,预设MCMC抽样次数为2500次。截去前500数据,使用后2000抽样样本对参数的后验密度进行估计。为了验证抽样链条可以有效地估计参数的后验密度,使用Geweke统计量[12]对MCMC抽样链条的收敛性进行检验,检验方法是将抽样链条作为时间序列数据,取前10%数据作为子序列1,后50%数据作为子序列2,比较两条子序列均值差异程度。检验统计量为:

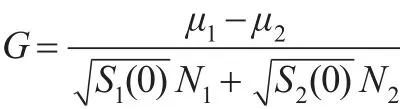
其中μ1和μ1分别是两序列的均值;N1和N1为两子序列的样本量;S1（·）和 S2（·）为两子序列的谱密度函数估计。如果统计量绝对值大于2,就说明链条不收敛。表1给出了样本量为500时变点时刻k在各分位数上抽样链条的检验结果，表明链条均是收敛的。

表1 参数k抽样链条的Geweke检验结果

图1给出了样本量为500时的抽样结果,可以看出抽样链条比较稳定。

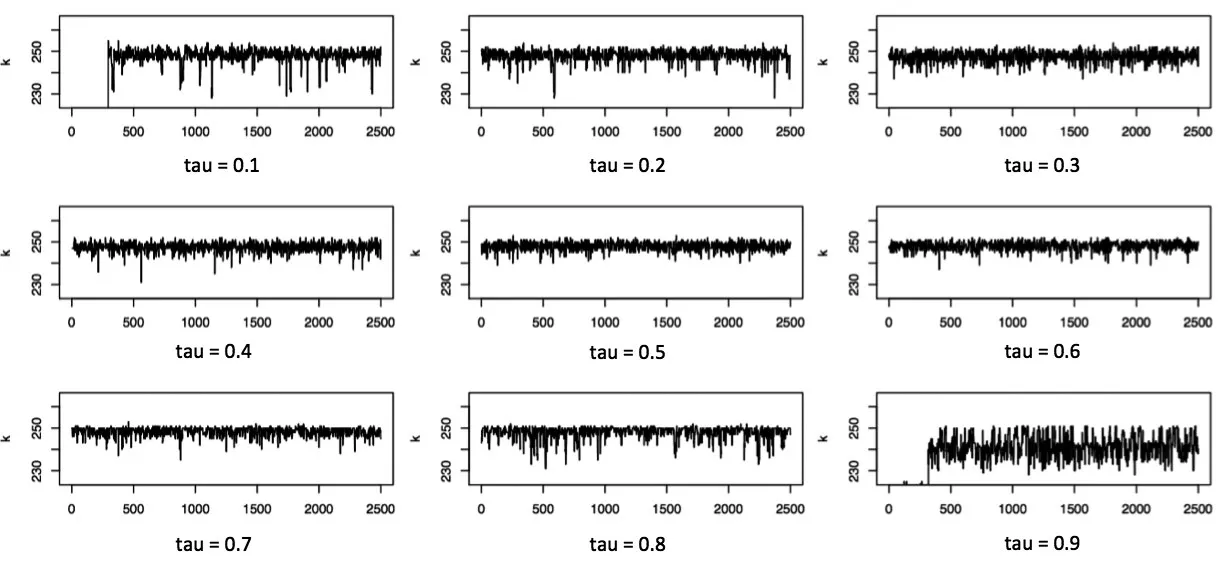
图1 样本量n=500时k在各分位数（tau）下的MCMC抽样结果

表2给出了在样本量分别为200、300和500时,在各分位数上变点相对位置k/n估计的均方误差（MSE）。使用数据k/n是为了保证不同样本量下得到估计结果的MSE的可比性。

表2 不同样本量下抽样链条的MSE

同之前所有分位数模型的估计方法一样,当样本量较少时,在高低两侧分位数上会存在有效样本量过少的问题。随着样本量增加，各分位数上的MSE明显下降，而当样本量大于或等于500时，MSE已经非常小了。

4 实证分析

4.1 数据

本文针对2013年8月底到2015年底的中小板综合指数极差数据建立具有单个变点的分位数自回归模型。在非主板市场中，中小板股票市场一直是波动性较大的板块。从表3可以看出,相对于中小板综指极差数据的均值,标准差的数值表明了市场的波动性比较大;通过偏度和峰度可以知道数据具有右偏以及尖峰厚尾的性质。而Jarque-Bera统计量在1%的水平上是显著的,说明数据并不服从正态分布。而传统条件均值模型无法刻画出这些特征,对极端值也没有很强的稳健性。下页图2给出极差数据的时间图。

表3 中小板极差数据基本描述统计量

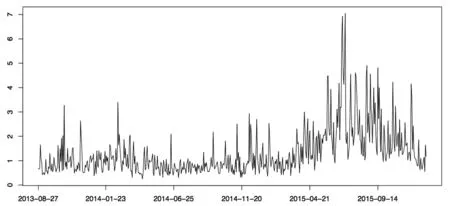
图2 中小板极差时间图

根据Koenker和Xiao（2006）所使用BIC信息准则对变量进行选择。用4阶分位数自回归对数据进行建模是合适的（见表4）。

表4 BIC变量选择

4.2 实证结果

在对实证数据建模时,MCMC抽样次数预设为5000次,参数后验密度使用链条后4000数据进行估计。

表5给出了对实证数据建模得到的估计结果（由于篇幅原因，表中只给出了变点时刻和各阶滞后项系数之和，即模型单位根的估计值），表6是链条收敛性的Geweke检验结果。记变点时刻前的系数为 θ1=（a0，a1，a2，a3，a4）,变点时刻后的系数记为 θ2=（b0，b1，b2，b3，b4）。结果表明各参数的抽样链条都是收敛的。

表5 估计结果

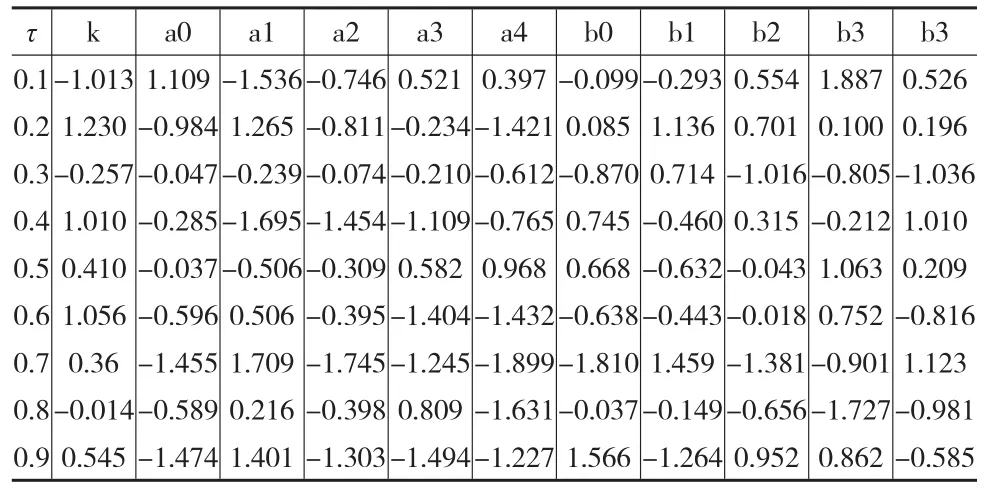
表6 参数k抽样链条的Geweke检验结果

图3表明，在高分位数上变点发生时刻较早,从0.6到0.9位数上均为2015年3月16日。而在从中间分位数一直到低分位数上,变点的估计时间滞后了一到四周,在最低分位数τ=0.1上为2015年4月14日。图4画出了在不同分位数上变点时刻前后的自回归模型单位根的估计。可以明显地看出，在较高的分位数上，中小板极差数据有相应较高的单位根；在变点后单位根（b1）比变点前（a1）大，并且在不同分位数上，表现出分位数越高差别越大的趋势。在变点后的0.8和0.9分位数上，单位根已经分别达到0.978和1.104。

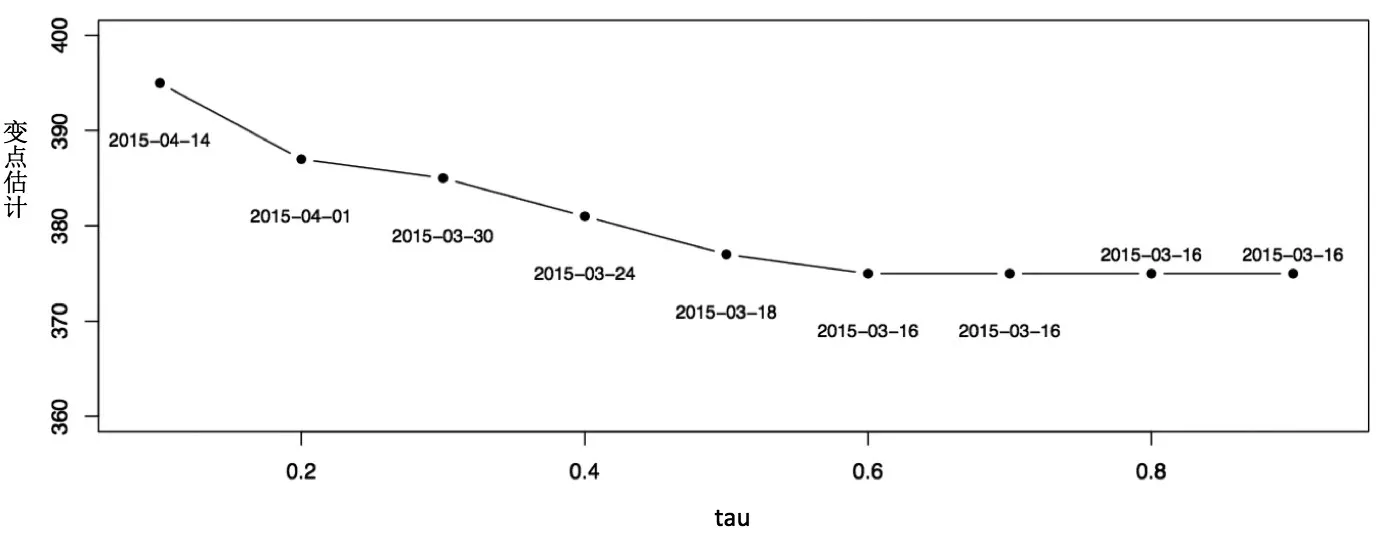
图3 在各分位数（tau）上变点时刻k的估计结果

图4 在各个分位数（tau）上变点时刻前后单位根的估计结果

5 结果分析

不同于主板市场,中小板市场通常会出现比如信息披露不及时、公司利润数据造假以及一直较高的IPO抑价率等现象,所以对于中小板市场的学术研究大多都关注于该市场收益的波动性。作为我国资本市场的重要组成部分,中小板市场给企业和投资者带来了更多的直接融资和投资的机会。也正因为如此,该市场投机氛围对市场波动性的影响也一直受到广泛关注。

对图3和图4中估计结果的解释如下:随着分位数的增高,各自回归项系数之和增大,说明在波动性增加的情况下,市场的大幅波动有更强的滞后性,并且伴随着更高的膨胀（单位根非平稳）性,突变也较早地发生在高分位数,即在市场波动较大时;在低分位数上,自回归滞后项系数相应较小,说明市场在波动幅度较小时,波动程度的滞后性较弱,相应检测出的变点位置也更迟一些。

从高分位数到低分位数，对变点时刻的估计从2015年3月16日到4月14日。在这近一个月的时间内，中小板综指开启了剧烈的涨势。事实上从2015年初该指数已经开始呈现较为平稳的上涨趋势，而投资者在此期间表现出非常积极的投机情绪。图5是中小板综指的成交量数据时间图，图中实心三角符表示对该板块估计出的最早的变点时刻。

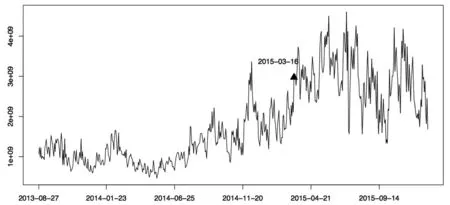
图5 中小板综指成交量数据时间图

在变点时刻之前，指数的成交量数据从2014年下半年以来已经处于涨势，表明了市场的投机情绪一直处于积极上涨状态，而市场的波动数据在各个分位数上是平稳的（图2）；而在变点时刻之后，成交量数据波动突然变大，说明了在这段时间内，投资者的投机情绪是十分不稳定的。数据向上和向下的波动幅度都很大，说明市场中同时存在正负两向态度差别很大的投机情绪。由于不同态度的投资者对收益预期、风险容忍度以及投资策略的异质性给市场带来了剧烈变化，在变点时刻之后市场的波动性开始大幅增加，特别是在高分位数上，数据的平稳性已经被打破（图4）。

6 总结

用分位数自回归模型在对时间序列数据进行建模时，能较好地捕捉到数据动态的非对称性，以及在长期保持平稳的前提下，出现的局部单位根非平稳现象。研究加入变点的分位数自回归模型，不仅可以刻画模型在不同分位数上结构的突变情况，而且可以反映出数据的信息滞后性和非平稳性在变点出现前后的差异。

由于分位数自回归模型分布假设的复杂性，使得对加入变点之后的模型进行贝叶斯分析时，一般很难写出各参数后验分布的解析表达式。本文给出模型参数的MCMC抽样算法，解决了这一问题。通过仿真实验，验证了MCMC抽样方法对于分位数自回归变点模型估计的有效性。

对于中小板综指的极差数据，成功地检测出了序列结构在不同分位数上的突变时刻，并估计出变点前后各分位数上模型的滞后项系数，表明在变点时刻前后数据的信息滞后性和各分位数上的单位根非平稳性的变化。结合中小板综指的成交量数据，分析了在中小板市场投资者的投机情绪的变化和市场波动性突变之间的相互影响和作用，从市场投机层面解释系数变点检测结果的经济意义。

[1]Koenker Roger,Gilbert Bassett.Regression Quantiles[J].Econometri⁃ca,1978,46（1）.

[2]Koenker Roger,Xiao Z.Quantile Autoregression[J].Journal of the American Statistical Association,2006,101（475）.

[3]Hideo Kozumi,Genya Kobayashi.Gibbs Sampling Methods for Bayes⁃ian Quantile Regression[J].Journal of Statistical Computation and Simulation,2011,81（11）.

[4]陈耀辉,郭俊峰,殷文超.人民币升值对中小板市场波动的影响——基于贝叶斯分位数回归的分析[J].系统工程,2015,33（1）.

[5]LY Vostrikova,Detecting’Disorder’in Multidimensional Random Processes[J].Soviet Mathemat-ics Doklady,1981,（24）.

[6]陈希孺.只有一个转变点的模型的假设检验和区间估计[J].中国科学,1988,（8）.

[7]宿成建,陈洁.应用变点模型来研究沪深股股市波动性突变行为[J].重庆大学学报,2003,26（10）.

[8]叶五一,缪柏其,谭常春.基于分位点回归模型变点检测的金融传染分析[J].数量经济技术经济研究,2007,24（10）.

[9]叶五一,缪柏其.基于Copula变点检测的美国次级债金融危机传染分析 [J].中国管理科学,2009,17（3）.

[10]王维国,宿成建,王霞.基于贝叶斯推断的上证指数突变点研究[J].中国管理科学,2009,17（3）.

[11]Efthymios G.Tsionas.Bayesian Quantile Inference[J],Journal of Sta⁃tistical Computation and Simulation,2003,73（9）.

[12]J Geweke.Ecaluating the Accuracy of Sampling-based Approaches to the Calculation of Posterior Moments[J].Sta Report,1991,（4）.