独立二项分布序列变点的识别方法

赵江南， 庞 冬， 樊森德

(新疆农业大学 数理学院，新疆 乌鲁木齐 830052)

引 言

由于变点问题涉及经济、医学、金融、工程等很多领域，所以估计一个随机序列中变点的位置是近年来统计学的热点研究问题之一。研究变点问题的方法有很多种，文献[1-2]用MCMC方法研究了IIRCT情况下二项分布、威布尔分布的多变点问题，文献[3]用IBF算法研究了正态分布均值单变点的识别问题等等。但对独立二项分布序列变点的研究的还比较少。本文运用IBF算法研究二项分布的变点问题，给出了识别变点个数和通过IBF算法识别变点具体位置的步骤，随机模拟的结果表明估计值较为精确。

1 独立二项分布序列变点模型

考虑如下具有独立二项分布序列变点模型，假设各yi相互独立

假设ti已知，当θ1≠θ2≠.....≠θk+1(未知)时，我们称此模型为一个具有k个变点且变点位置为ri,(i=1,2,..,k)的独立二项分布序列变点模型。那么，我们的问题是如何判断序列{yi}(i=1,2,..,n)中的变点个数k，以及确定变点的位置ri,(i=1,2,..,k)。

下面通过IBF方法估计变点的位置ri,(i=1,2,..,k)

2 IBF方法

在应用IBF算法估计变点的位置ri,(i=1,2,..,k)之前，首先介绍IBF算法。Tian通过一种非迭代Bayes抽样方法，简称IBF方法，来从一组观测数据中推导出缺失数据的条件分布，然后从完整数据的后验分布中提取样本，进而判决缺失数据的统计分布。

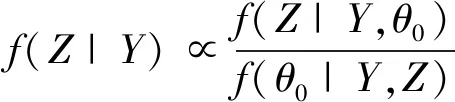
(1)

对于任意θ0∈S(θ|Y)及所有Z∈S(Z|Y)成立。证明见[10]。其中f(Z|Y)为缺失数据的后验分布，f(Z|Y,θ)为缺失数据的条件后验分布，f(θ|Y,Z)为参数θ的后验分布。(1)式表明，缺失数据的后验分布f(Z|Y)正比于f(Z|Y,θ)与f(θ|Y,Z)的商。因此要想得到缺失数据的统计分布，只需得到f(Z|Y,θ)及f(θ|Y,Z)即可。

3 通过IBF方法识别变点位置ri,(i=1,2,..,k)

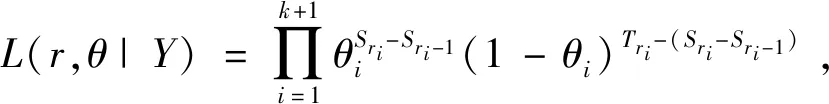
(2)

(3)

又因为r0=0，rk+1=n，所以

(4)

将变点r看做(1)式中的缺失数据，那么由(1)式得

(5)

基于(5)式，我们就得到了变点的位置的后验分布，可以依照此式对变点位置做精确的统计推断。下面我们通过Bayes因子讨论如何确定序列中变点的个数。

4 通过Bayes因子确定变点个数k

根据文献[12]，Bayes因子定义如下：

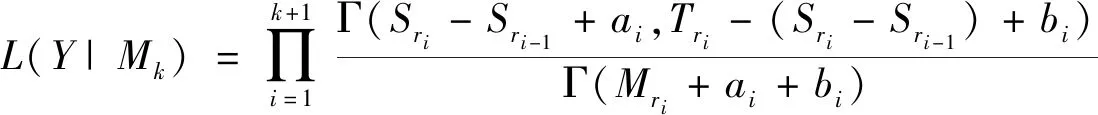
Jeffreys在1961年的附录B中给出了用Bayes因子进行模型选择的一般准则，他指出当BFs+1,s落在(1,3.2),(3.2,10),(10,100),(100,+)这四个区间时分别代表s与s+1间的差别不值一提、较为肯定支持s+1、强烈的支持s+1、以及较为强烈的支持s+1。

5 随机模拟

经计算得L(Y|M1)=3.334×10(-75)，L(Y|M0)=9.750×10-88，所以BF1,0=3.420×1012，因此，我们判断模型为具有一个变点的独立二项分布序列。再由(1)～(5)得变点在各处的概率分布见表2(精确到小数点后三位)。

表1 模型一随机变量序列

表2 变点r的分布律

表中带*为概率最大的变点位置，即判断出变点位置r=10。

第二个变点模型为

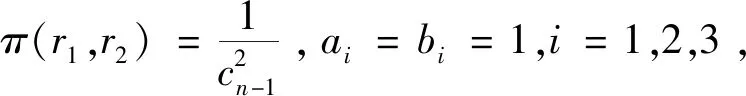
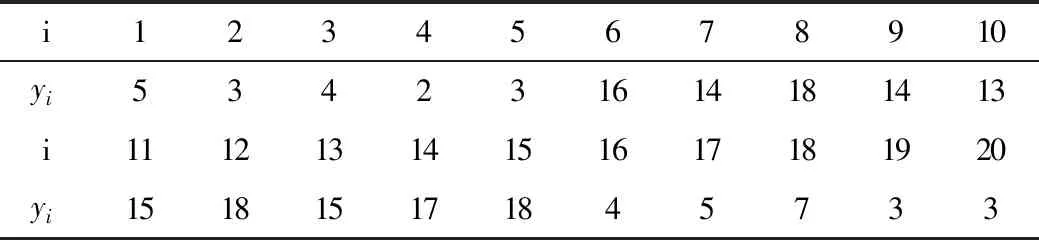
表3 模型二随机变量序列

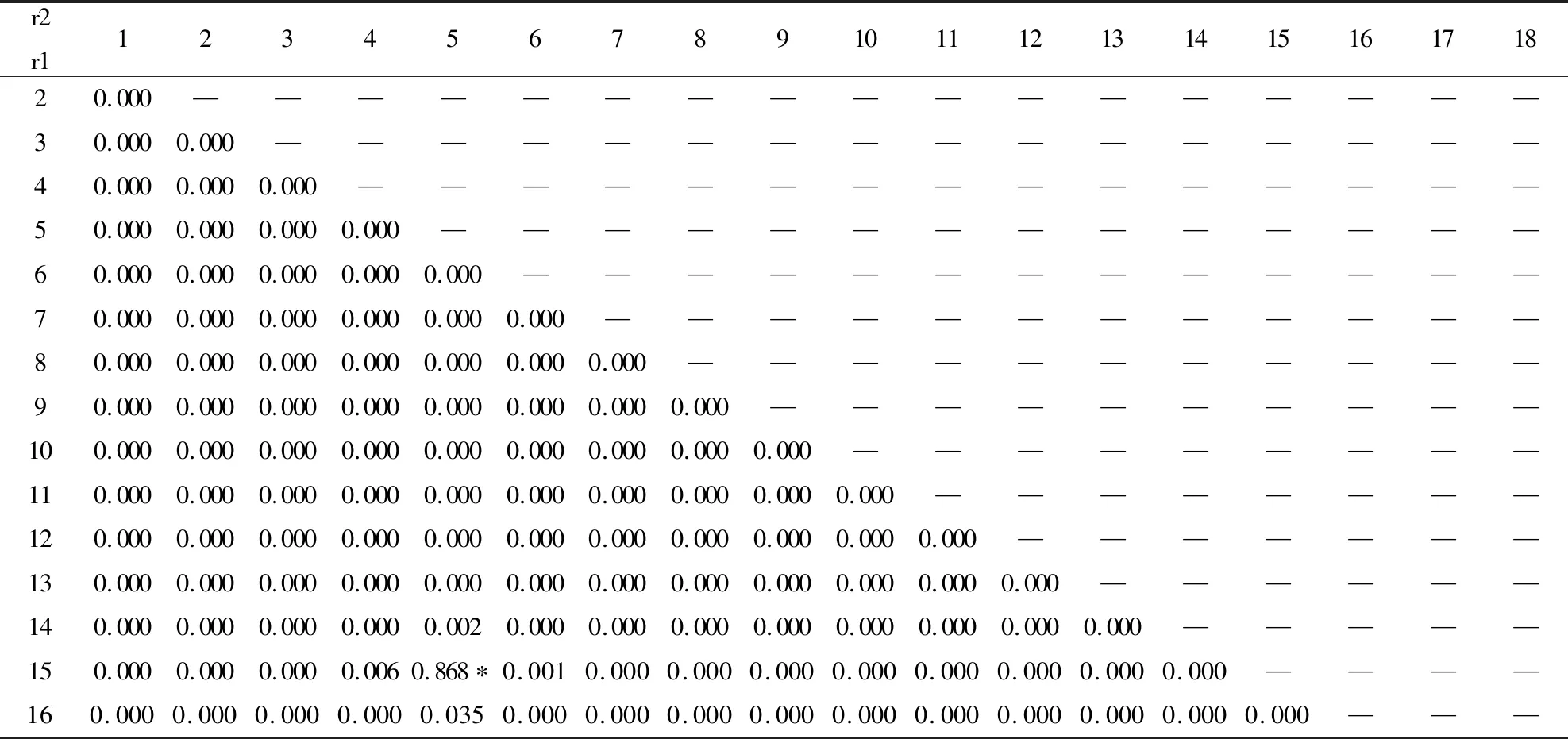
表4 变点联合分布律

续表4

r2r1123456789101112131415161718170.0000.0000.0000.0000.0080.0000.0000.0000.0000.0000.0000.0000.0000.0000.0000.000——180.0000.0000.0000.0010.0750.0000.0000.0000.0000.0000.0000.0000.0000.0000.0000.0000.000—190.0000.0000.0000.0000.0000.0000.0000.0000.0000.0000.0000.0000.0000.0000.0000.0000.0000.000

表中带*为概率最大的变点位置，即判断出变点位置 r1=5,r2=15。

6 实证分析

6.1引用[7]中Hanify在1981年分析的数据：1960年到1976年新西兰北部某地区怀孕第一个月出现畸形足的人数xi及当年新生儿总数ni(见表5)。

表5 1960年到1976年某地区怀孕第1个月出现畸形足的人数及新生儿总数

接下来通过IBF方法，为了简化计算量，首先将数据xi及ni取常用对数，得到BF10=562.621，所以选择单变点二项序列模型。然后由(1)～(5)得后验概率最大的点为x6，即1965年，后验概率为0.193，结合Worsley在1983年分别用似然比法和CUSUM检验法得到的变点位置在第6个，结果基本一致。事实上，在第6个观测数据即1965年也是在该地区首次发现使用2,4,5-T除草剂的年份，此后出现畸形足新生儿比率明显升高。由此可以推断，该种除草剂与出现畸形足患儿有很大相关性。

6.2引用Smith[12]在1982年分析的数据，在13个按时间顺序排列的中世纪手稿中观察到的两种代词词尾的出现次数。一套手稿中的13个文件被认为是多个作者的工作，因为每个文件中每个结束的比例似乎在顺序上有所不同。因此，假设这些文档可以分为时间上连续的阶段，每个阶段都有一个独特的结尾比例，例如，对应于不同的抄写员，一个离散多变点模型适用于这些数据，y1i,y2i,ni分别代表第i个文件里两种代词词尾的出现次数以及总数数据如表6。

表6 中世纪手稿中观察到的两种代词词尾的出现次数

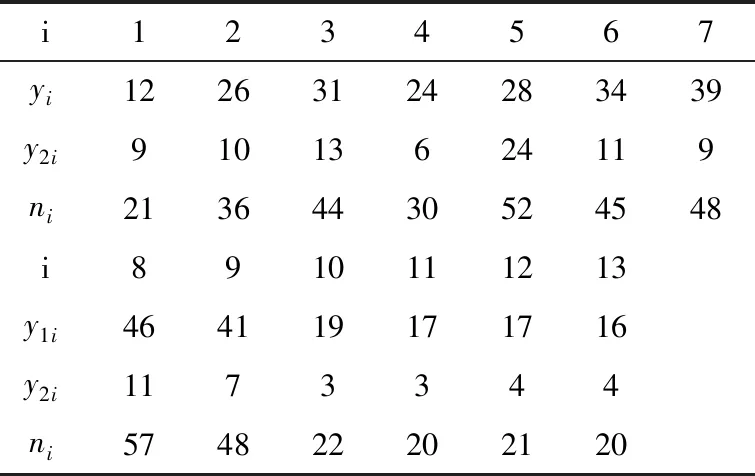
i1234567yi12263124283439y2i91013624119ni21364430524548i8910111213y1i464119171716y2i1173344ni574822202120

首先考虑三个模型分别是没有变点的独立二项序列模型；含有一个变点的独立二项序列模型以及含有两个变点的独立二项序列模型。其中BF1,0=212.064；BF2,0=673.952；BF2,1=3.178，再综合前人结论，因此我们选择含两个变点的独立二项序列模型。然后由(1)～(5)得到概率最大的变点位r1=4，r2=5，最大概率为0.328。这与Smith[12]以及D.A.Stephens[9]所得结果一致，因此可以判断此部手稿为三名抄写员抄写。

7 结语

本文通过Bayes因子以及IBF方法实现了对独立二项分布序列变点模型的变点个数和变点位置的估计。给出了推导的详细步骤，并通过随机模拟验证了估计的准确性，再结合实例，将分析应用到了现实生活，实现了对两个现实中存在的独立二项分布序列变点模型的估计。结果显示，估计精确，得到的结果与前人一致。