正态分布序列均值变点检测的贝叶斯方法

郭卫娟

(湖北第二师范学院 数学与经济学院；大数据建模与智能计算研究所,武汉 430205)

1 方差已知的的正态分布序列变点问题简介

(1)

若通常称为多未知变点模型，对于多个未知变点模型，我们要解决的问题主要有两个，第一是确定变点的个数；第二是确定变点的具体位置，实际上变点的数目完全由变点的位置所决定，通常我们采用二分法来确定，其基本想法是首先我们只考虑仅有一个变点的模型，利用某种方法确定这个变点的具体位置，然后以此位置作为分界点，将全部数据集分成两个不相交的子集，对于每个子集，按照前面的方法重新判断，看看每个子集中是否存在变点，该过程一直进行到不再有变点为止。利用该方法，我们可以将原来模型简化为没有变点和仅仅只有一个变点的模型，下面我们按照贝叶斯统计学方法给出一个数据集有无变点和仅有一个变点时确定其位置的方法。

2 贝叶斯信息准则

(2)

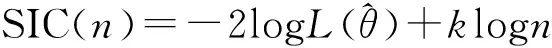
(3)

而AIC和SIC的区别在于常数项惩罚项上，实际上，BIC给出了真实模型的渐近一致估计，因此在实际上应用较AIC更为广泛。利用信息准则来估计变点的有无和位置较为实用和简单。考虑到本文主要用贝叶斯方法来研究变点问题，而所有的贝叶斯统计推断都是基于参数的后验分布进行的，因此可以将似然函数即经典统计中的样本联合概率密度函数修正为贝叶斯后验概率密度似然函数，因此得到变点的贝叶斯信息准则为BSIC(n)(y表示可以观察到的样本数据，通常用向量表示):

(4)

令H0表示无变点，令H1表示有唯一的变点，下面分布计算这两种情况的贝叶斯信息准则，

3 无变点下的正态序列的贝叶斯信息准则

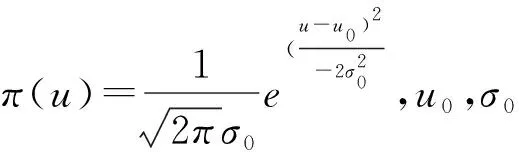
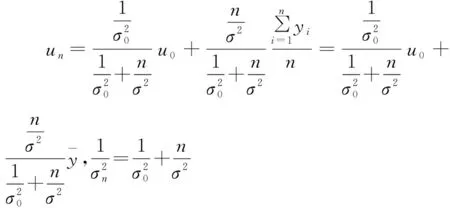
(5)

(6)

4 仅有一个均值变点的正态序列的贝叶斯信息准则

此时模型(1)被简化为：

显然该模型中含有三个未知参数u1，u2，k，其中我们感兴趣的参变点的位置数k，而u1，u2是我们不感兴趣的参数，在贝叶斯统计中一切未知参数都是当作随机变量，称为多余参数或者叫讨厌参数，为了去掉多余参数的影响，我们必须对它加合适的先验分布以便积掉。为此假设

(7)

又因为根据已知信息，只有唯一的变点，其可能位置为1，2，…，n-1，因为没有任何先验信息，利用同等无知原理，应假设唯一的变点在1，2，…，n-1上服从均匀分布，由此得到变点的位置的先验为：

(8)

此时利用正态分布密度的正则性，不难计算出完整的后验概率密度为：

(9)

(10)

(11)

5 唯一变点位置的判别

按照贝叶斯理论任何统计推断都因该基于后验分布进行，为此计算以上先验下三个参数u1，u2，k的后验分布。(9)式可以看成是在y1，y2，…，yn给定的条件下参数u1，u2，k的联合后验分布，利用边缘分布和联合分布的关系，可以计算出：

(12)

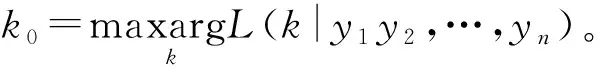
同时利用11式，可以计算出其他两个参数u1，u2的后验期望为：

这说明参数u1，u2的后验期望估计和前面求出的参数的极大似然估计也一致。

最后我们来看看数据拟合结果：

也就是用R软件生成方差已知均值不同分布的正态分布的随机数，然后利用上面的算法识别有无变点，在有变点的情况下，估计变点的具体位置；

下面以3个变点为例，也就是模拟样本的真实变点在100、200的第300个位置上，总共抽取400个样本。说明本次随机模拟的结果：

为方便起见，本题中各个部分均值的差别越大，这样做的目的是为了区分各个变点的显著性，易知，在上面理论假设之下，识别的变点依次为300,200,100，这和实际情况完全吻合。因为以上总体方差都相等，这说明各组数据波动性相差不大，而在300这个位置上，前后均值差为4，是各部分差最大的，因此最先识别出来。因此本方法还是比较有效，尤其是在区别差异大的不同总体上。当然，缺点也是明显的，就是计算量比较大，这也是任何贝叶斯方法的共性缺点。总的来说，贝叶斯方法对很多统计问题提出了一个粗略的近似解，所以该方法随计算机计算能力的日益发展而展现出更多的用处。