基于密码算法的压缩感知测量矩阵构造

谢 冬， 郭东升， 叶四军

(1.安徽师范大学 计算机与信息学院，安徽 芜湖 241003;2.安徽省新芜经济开发区 管理委员会，安徽 芜湖 241000)

引 言

压缩感知理论(Compressed Sensing,CS)是由E.J.Candes、J.Romberg、T.Tao和D.L.Donoho等科学家于2004年提出[1]，其已被应用于各个相关领域，如图像处理[2]、医学成像[3]、地质勘探[4]、密码学[5]以及人脸识别[6]当中。CS的核心思想基于以下两点：(1)信号的可稀疏化结构特征。传统意义上的Shannon信号表示方法只利用了最少采样信号的先验信息[7]，并没有考虑到信号的稀疏结构。(2)信号的可压缩特性。在信号稀疏性的基础上，以远低于Nyquist采样率的随机采样来获取信号的离散样本，然后通过非线性优化算法来重构信号[8]。

测量矩阵在CS中的数据采样和信号重建步骤都起着至关重要的作用，它的性质几乎决定了原始信号的全局信息能否保存下来[1,7,8]。测量矩阵的构造方法主要分为随机性构造[9]和确定性构造[10]两种。常用的随机测量矩阵有高斯随机测量矩阵[11]、贝努利随机测量矩阵[12]等，其特点是元素都是独立地服从某种随机分布。随机测量矩阵具有不确定性，且浪费存储资源，使得其实际应用受到限制。在保证准确重构的前提下，确定性构造方法可以大大地降低系统的存储空间。Haupt等人提出托普利兹矩阵[13]与循环矩阵[14]两个确定性测量矩阵的构造方法,它们是通过有限个确定性向量循环构造而成。Devore提出多项式确定性测量矩阵[10]，其利用多项式系数在有限域中遍历取值的结果来构造矩阵。然而，与随机测量矩阵相比，确定性测量矩阵在重建效果上存在一定差距，同时对信号的稀疏度也有较高要求。

CS不但具有压缩特性，而且具有一定的加密属性[15]。但是，本文的目标并不是运用压缩感知来构造密码算法，而是从一个相反的角度，即运用常见的密码算法(如分组密码DES与AES算法)来构造CS的测量矩阵。具体地，首先运用这些密码算法产生伪随机序列，然后将这些伪随机序列按照一定的方法依次填充到测量矩阵之中。其次，运用密码算法构造的压缩感知测量矩阵来压缩图像信号得到测量图像。最后，通过经典的OMP算法来重构原始图像[16]。实验结果表明，与传统的测量矩阵(如高斯矩阵、混沌矩阵)一样，基于DES、AES以及M序列等密码算法产生的测量矩阵具有较好的重构效果。

1 基础理论

1.1 压缩感知

基于自然界大多数信号可稀疏化的特点，压缩感知理论突破了传统的尼奎斯特采样定理，在保证完美重构的前提下，以更小的采样率来采样信号，在采样的同时就抛弃了冗余信息。其具体过程如下：

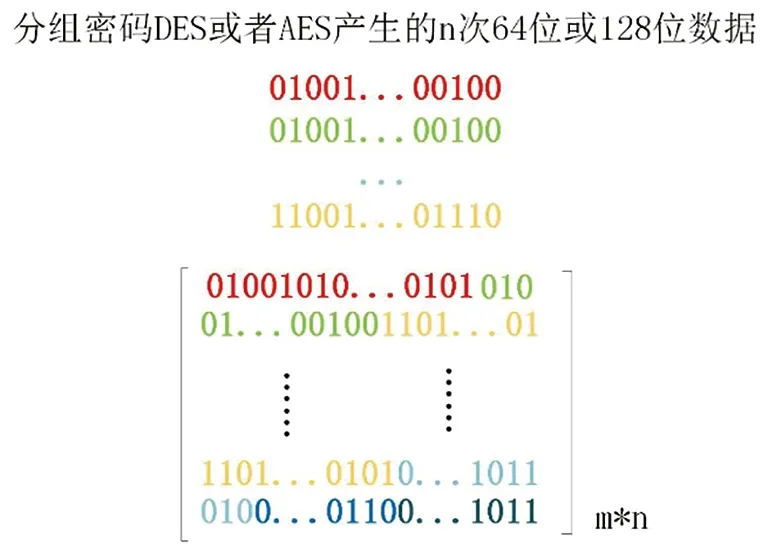
设信号α∈Rn，在某组正交基Ψ∈R(n×n)下是稀疏的，即α=Ψx，其中x∈Rn是稀疏的。若向量x中有k个非零实体，则称x是k稀疏的。可用测量矩阵Φ∈R(m×n)(m

Y=Φα=ΦΨx=Ax。

(1)

其重构可用最小化l0范数来求解：

(2)

当测量矩阵A满足约束等距特性时[17]，可以将(2)式等价地转换为最小化l1范数问题：

(3)

对于最小化l1范数问题，已有相关算法对其求解，如OMP算法[16]。

1.2 常见的密码算法

DES是一种常用的分组密码算法，其明文分组、密文以及密钥均为64位(有效密钥长为56位，其中密钥有8位是奇偶校验码)。其核心思想是采用Feistel网络结构进行16轮迭代，从而达到混淆与扩散的效果。为了克服DES短密钥的缺陷，NIST于2001年发布了AES算法。AES的分组长度为128位，密钥长度分别为128位、192位、256位。本文采用128位密钥的AES算法，共需10轮迭代运算。

线性反馈移位寄存器是构造序列密码体制的常用工具。M序列是指能够达到线性反馈移位寄存器最大周期的序列。若n1为移存器级数，则最大周期为2n1-1。一个M序列由线性递推式与初始状态两个因素决定。

2 基于密码算法的测量矩阵构造

本文将基于分组密码算法(DES与AES)与序列密码算法，来构造CS的测量矩阵。通过这些密码算法产生伪随机序列，然后将这些伪随机序列按照一定的规则依次填充到测量矩阵之中。

2.1 AES、DES算法构造的随机测量矩阵

基于分组密码的测量矩阵构造方法可通过如下形式进行：

①根据测量矩阵的维数，随机产生等长的分组密码密文。若测量矩阵A为m×n阶矩阵，则需要随机选择分组密码的密钥以及长度为mn的明文比特，通过分组加密产生mn个密文比特输出。

②将生成的随机密文比特在矩阵中依次排列，如果超过A中行的长度，就下移到下一行，不断填充，直至A填满为止，如图1所示。

图1 基于DES或AES构造测量矩阵方法

2.2 M序列构造的随机测量矩阵

基于序列密码体制的测量矩阵构造方法可通过如下形式进行：

①根据测量矩阵的维数，随机产生等长的M序列。若测量矩阵A为m×n阶矩阵，则需要随机选择一个可产生M序列的n1级非线性反馈移位寄存器f(x)，其中n满足2n1≥mn+1。

②随机选择初始状态s0，由f(x)与s0产生mn个比特位。

③将生成的随机比特串在矩阵A中依次排列，如果超过A中行的长度，就下移到下一行，不断填充，直至A填满为止。

3 实验分析

3.1 正确性

选择三个256×256的原始图像，分别是(a)海螺、(g)赫本以及(m)青竹。选用的测量矩阵分别是标准的高斯随机矩阵、Logistic混沌矩阵以及本文提出的DES测量矩阵、AES测量矩阵与M序列测量矩阵。其中Logistic混沌矩阵中初始值为x0=0.2915826302。产生M序列测量矩阵的反馈移存器的本原多项式系数是

[1000000000000001]，初始值为[0000000000000001]。在电码本工作模式(ECB)下，随机选择DES与AES的明文信息。DES测量矩阵和AES测量矩阵的具体参数如表1和表2所示。

表1 构造DES测量矩阵的具体参数(16进制)

表2 构造AES测量矩阵的具体参数

发送端将原始图像通过压缩感知进行压缩加密处理，接收端运用OMP重构算法对密文图像进行解密重构，得到的图像如图2所示。

图2 不同测量矩阵的重构效果(a),(g),(m)原始图像；(b),(h),(n)M序列测量矩阵恢复图像；(c),(i),(o)DES测量矩阵恢复图像；(d),(j),(p)AES测量矩阵恢复图像；(e),(k),(q)高斯随机矩阵恢复图像；(f),(l),(r)Logistic混沌矩阵恢复图像。

从视觉的角度可以看出，基于分组密码与序列密码体制构造的矩阵与传统的测量矩阵一样，均能被用作压缩感知的测量矩阵。为了定性的表示图像的恢复性能，本文通过峰值信噪比(Peak Signal to Noise Ratio,PSNR)来评价图像重构的效果。PSNR的公式计算如下：

PSNR=10×log10((2n-1)2/MSE),

(4)

其中n是每个采样值的比特数，MSE是原图像与处理图像之间均方误差。由表3可知，M序列、DES算法、AES算法、Logistic混沌系统以及高斯分布产生的随机测量矩阵，都具有较好的重构图像的能力。

表3 不同测量矩阵加密后恢复图像的PSNR值

3.2 密钥的敏感性

为了防止敌手的猜测攻击，密码系统应当具备密钥敏感性。在提出的方案中，消息发送端与接收端均运用密钥K产生DES测量矩阵、AES测量矩阵以及M序列测量矩阵来加解密图像。假设明文是正确性实验中的(m)青竹，DES密钥是KDES=0E6A03CE647D513C。若公开信道存在一个攻击者，猜测的密钥KDES*与真实值KDES差2比特，即KDES*=0E6A03CE647D513E。其重构效果如图3所示。图3同时展示了若AES测量矩阵与M序列测量矩阵改变密钥1bit时的重构效果。结果表明M序列测量矩阵、DES测量矩阵以及AES测量矩阵三种加密算法具备密钥敏感性。

图3 不同算法的真假密钥重构图像的效果：(a)-(c)M序列、DES算法以及AES算法密钥为假密钥的重构图；(d)-(f)M序列、DES算法以及AES算法密钥为真密钥的重构图。

3.3 测量次数对PSNR影响

在压缩感知理论中，测量次数影响着重构效果。本实验选择“青竹”作为明文，运用M序列、DES算法以及ECB、CBC、OFB这三种模式的AES算法来研究测量次数对PSNR的影响。针对明文“青竹”，采用4.1节的参数，实验结果表明密码学测量矩阵的重构效果最好的是DES测量矩阵，AES次之，M序列相对最差。但总体说来，随着测量次数的增大，PSNR整体逐步上升。

图4 测量次数对重构效果的影响

4 结 论

与传统的基于压缩感知来构造密码方案不同，本文基于对称密码算法AES与DES以及M序列等密码学本原，提出了一种构造压缩感知测量矩阵的方法。其主要的理论依据是这些密码学本原都可以产生伪随机的序列，若我们将这些伪随机序列填充到矩阵里，矩阵列与列之间的相关性均较低，其满足压缩感知测量矩阵的基本特征。实验结果表明，提出的密码学测量矩阵对图像信号具有良好的重构能力。