格兰杰因果检验中不同检验方法的功效比较

范传棋，范 丹

（西南财经大学 中国西部经济研究中心，成都 611130）

0 引言

Granger（1969）[1]以信息集为基础给出了因果关系的定义：如果序列At中含有预测序列Bt+j的信息（A有助于解释B未来的变化），则A是B的格兰杰原因。根据这一定义，学者们提出了多种检验格兰杰因果关系的思路。Sims（1972）[2]研究发现，如果A不是B的格兰杰原因，那么A关于B未来值的回归方程中具有一组相等的系数，它们并非显著地不同于零。Hslao（1979）[3]找到了两种更为简便的格兰杰因果检验方法：零元素法和过度拟合法。零元素法是通过直接证明矩阵中相关元素是否趋零，从而检验序列间格兰杰因果关系存在与否。过度拟合法是拟合一个更高滞后阶模型，通过构建LR统计量（进行似然比检验），从而判别序列之间有没有格兰杰因果关系。

基于以上思路，F、LR、Wald、Mwald统计量被用于序列间的格兰杰因果检验中。从实践上看，大样本情况下F、LR、Wald、Mwald统计量的检验效果相对较好，然而在小样本条件下一些统计量会面临检验效果不佳的问题。Toda和Phillips（1993）[4]研究表明，在小样本条件下以瓦尔德原理为基础的Wald、Mwald统计量的渐进分布是非标准的。Toda和Yamamoto（1995）[5]、Lütkepohl（1996）[6]指出检验统计量的非标准渐进分布，会带来检验效果弱化的问题。同时，小样本条件下格兰杰因果检验可能还面临着难判、误判的风险。周建等（2004）[7]采用Monte Carlo模拟方法，证实了小样本条件下F检验容易遇到“真实关系”难以甄别的问题，特别是在样本小于20的时候，即使检验结果显示“不存在因果关系”，也难以断定真实的格兰杰因果关系是否存在。

从现有研究看，学者们已经关注到小样本条件下格兰杰因果检验中一些统计量存在检验功效不足的问题，然而他们对这些统计量在小样本条件下的适用性及检验功效的比较研究相对较少。针对上面的问题，本文运用Monte Carlo模拟方法，比较小样本条件下F、LR、Wald、Mwald四种统计量在检验格兰杰因果关系中的检验效果，同时考察随着样本量的变化不同计量呈现出来的检验特征。

1 基本理论

1.1 Granger因果检验中的VAR及ECM过程

根据Granger对因果关系的解释，首先定义二维的VAR（k）过程，过程由式（1）给出。

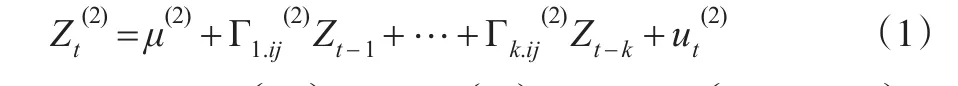
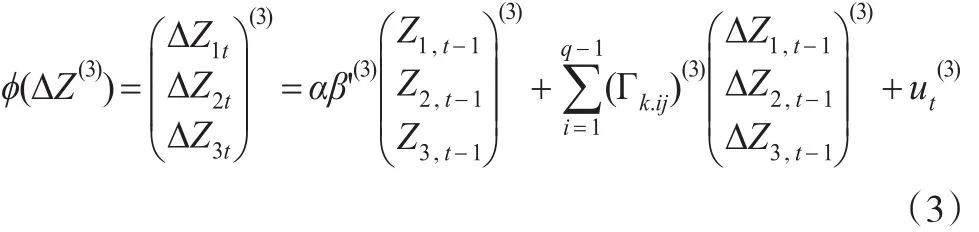
1.2 Granger因果检验中的统计量

1.2.1 F检验

以二维系统为例（三维系统同理类推），式（2）中（滞后1期，同理可以推导滞后2期）ECM表达式可以写成：对于式（4）中第1个方程，如果接受原假设 H（2）0∶则变量Z2t对Z1t的因果关系不存在；如果拒绝，则变量Z2t是Z1t的格兰杰因果原因。同理，这一定义也适合式（4）中的方程2。检验上述原假设的统计量为：

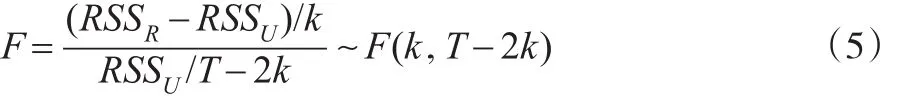
其中RSSR表示施加约束条件下模型的残差平方和，RSSU表示不施加约束条件下模型的残差平方和，k表示Z2t的最大滞后阶数，2k表示无约束模型中有待估的参数个数，T为样本容量。在满足高斯分布（多元正态分布）假定下，式（5）统计量渐进服从F分布。

1.2.2 LR（似然比）检验

以三维系统为例（二维系统同理类推），式（3）中（滞后1期，同理可以推导滞后2期）ECM表达式可以写成：

其中 Acj为 ΔZ1，t-j系数矩阵，Bcj为 ΔZ2，t-j系数矩阵，Ccj为 ΔZ3，t-j系数矩阵（c=1，2，3，j=1，2）。

对于式（6），ΔZct（c=1，2，3）之间的格兰杰因果检验原假设为其中 i=1，2，3 ；k=1，2，3…n ；同时，原假设还需要满足以下约束条件对于式（6）方程1，如果接受原假设 H（3）0 ，则 ΔZct（c=2，3）对ΔZ1t的格兰杰因果关系不存在；如果拒绝原假设H（3）0，则ΔZct是ΔZ1t的格兰杰原因。同理，这一原理也适合式（6）中方程2和方程3。检验统计量：

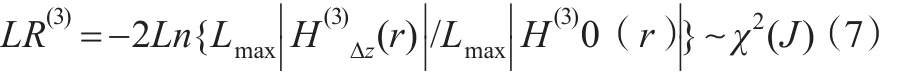
多维系统中（n≥2）的Wald统计量可以被表述为：

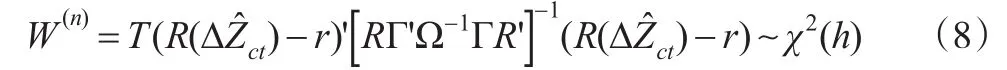
在满足原假设条件下，式（7）统计量渐进服从 χ2分布。

1.2.3 Wald及修正的Wald检验（MWald）

综合考察二维、三维系统，结合式（2）和式（3），给出检验 ΔZct（c=2 或 3）对 ΔZ1t是否存在格兰因果关系的一般性假设其中 R 为已知常数构成的矩阵，r是各元素为常数（通常是0或1）的矩阵。如果接受原假设，则 ΔZct对 ΔZ1t的格兰杰因果关系不存在；如果拒绝原假设H（C）0，则 ΔZct是 ΔZ1t的格兰杰原因，检验统计量为

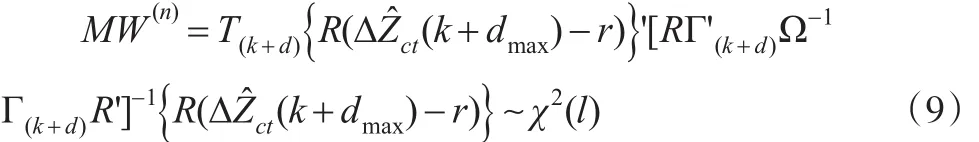
2 蒙特卡洛模拟试验设计

2.1 蒙特卡洛模拟的试验思路

结合以上的基本理论与检验思想，对二维、三维系统中的格兰杰因果关系进行蒙特卡洛模拟，将二维系统设计为拒绝原假设（即拒绝ΔZct不是ΔZ1t的格兰杰因果原因，表示序列之间存在格兰杰因果关系），将三维系统设计为接受原假设（即接受ΔZct不是ΔZ1t的格兰杰因果原因，表示序列之间的格兰杰因果关系不存在）。同时设定模型中最 长 滞 后 阶 Lag（ΔZct）=2 ，小 样 本 范 围 定 义 为显著水平设为 P=0.05 ，模拟次数设定为n=5000。为了考察F、LR、Wald及MWald统计量在小样本条件下检验功效的基本规律与样本特征，本文通过调整系数矩阵的形式完成数据生成过程。

2.2 数据生成过程（Data Generation Process，DGP）

在二维系统中，生成四种数据过程（DGP（1）、DGP（2）、DGP（3）、DGP（4））；在三维系统中，生成两种数据过程（DGP（5）、DGP（6））。 DGP（1）主要考察不存在滞后项情况下序列间不同检验方法在检验格兰杰因果关系中的检验功效；DGP（2）是在 DGP（1）基础上引入滞后1期）的模拟过程；DGP（3）是引入滞后 2 期）的模拟过程；DGP（4）是同时引入的模拟过程。同理，模拟三维系统中的 DGP（5）、DGP（6）过程，DGP（5）是引入（滞后1期）的模拟过程；DGP（6）是同时引入的模拟过程。

系数矩阵的生成过程借鉴周建和李子奈（2004）[7]在研究变量间格兰杰因果关系时提出的自举方法，当时他们构建了一个1阶滞后因果关系模型：ΔZ1t=aΔZ1，t-1+u1t，ΔZ2t=bΔZ1，t-1+cΔZ2，t-1+u2t，其中对 a，b，c 分别取0.1、0.5、0.9，形成了27种数据生成过程，最终选取了2个数据生成过程进行分析。在此基础上，本文将滞后阶延伸至2阶、序列拓展至三维，即 ΔZ1t=aΔZ1，t-1+bΔZ2，t-1+cΔZ3，t-1+dΔZ1，t-2+eΔZ2，t-2+fΔZ3，t-2+u1t（三 维 系 统），ΔZ1t=aΔZ1，t-1+bΔZ2，t-1+cΔZ1，t-2+dΔZ2，t-2+u1t（二维系统）；同时将二维和三维系统中的系数矩阵元素ξij限定在-1和 1 之 间 ，ξij∈[-1， -0.75， -0.50， -0.25，0，0.25，0.50，0.75，1]，通过系数矩阵元素的设定，形成了81种数据生产过程，最终在二维系统中选取了4种序列间存在格兰杰因果关系的数据过程、三维系统中选取了2种不存在格兰杰因果关系的数据过程（即二维系统中的 DGP（1）、DGP（2）、DGP（3）、DGP（4）和三维系统中的 DGP（5）、DGP（6）），数据生成过程如表1所示。

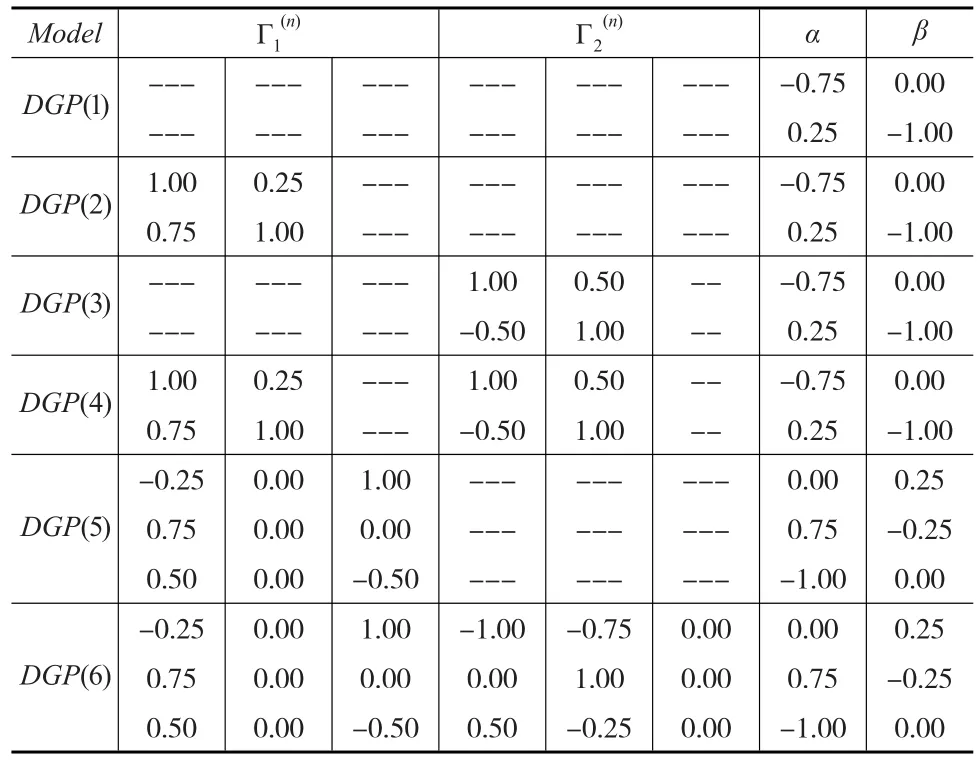
表1 蒙特卡洛模拟数据生成过程

2.3 F、LR、Wald、MWald统计量检验效果判定标准

在二维系统中模拟试验被设计为拒绝原假设，模拟中选取了存在格兰杰因果关系的数据过程，因此以F、LR、Wald及Mwald统计量显示“拒绝原假设”为检验效果判定的基本标准；具体而言，在显著水平P=0.05的条件下，F、LR、Wald及Mwald统计量的P值小于0.05时，被认为统计量显示“拒绝原假设”，在此基础上以统计量的P值趋近0作为检验效果最优的标准。同理，在三维系统中模拟试验被设计为接受原假设，模拟中选取了不存在格兰杰因果关系的数据过程，因为以F、LR、Wald及Mwald统计量显示“接受原假设”为检验效果判定的基本标准；具体而言，在显著水平P=0.05的条件下，F、LR、Wald及Mwald统计量的P值大于0.05时，被认为统计量显示“拒绝原假设”，在此基础上以统计量的P值趋近1作为检验效果最优的标准。

3 模拟结果分析

经过蒙特卡洛模拟，得到20、50、100、200、400位样本条件下F、LR、Wald及Mwald四个统计量检验序列间格兰杰因果关系时的P值（6种数据过程），如下页表2所示。

通过对表2分析，发现在小样本条件下（n≤ 400），F、LR、Wald、Mwald四个统计量在检验格兰杰因果关系时，检验功效存在差异。

（1）极小样本条件下，LR统计量检验功效最佳，MWald统计量检验效果最差。考察25位样本的情况，在二维系统中，模拟的是拒绝原假设（即我们期望统计量P值小于0.05）。从下页图1中可以看出，在0.05显著水平上显示“拒绝原假设”，效果最好的是LR统计量，效果最差的是 Mwald统计量。四种数据过程（DGP（1）、DGP（2）、DGP（3）、DGP（4））的 LR 统计量 P 值分别为0.047、0.043、0.061、0.043，这些值多数显示拒绝原假设；而四种数据过程的Mwald统计量P值分别为0.201、0.249、0.314、0.187，在0.05显著水平下这些值均显示接受了原假设，此时Mwald统计量产生了误判。在三维系统中，模拟的是接受原假设（即期望统计量值P更趋近于1）。从图2中可以看出，在各个统计量中显示“接受原假设”，效果最好的依然是LR统计量，效果最差的仍然是Mwald统计量。两种数据过程（DGP（5）、DGP（6））的 LR 统计量 P 值分别为0.933、0.956，这些值均表明显著地接受原假设；而两种数据过程的Mwald统计量值分别为0.646、0.625，这些值也表明接受原假设，此时Mwald统计量虽没有出现误判，然而其判定效果远远没有LR统计量好。另外，LR统计量、Mwald统计量在25位样本条件下呈现出来的特征，在50位样本条件下同样存在。

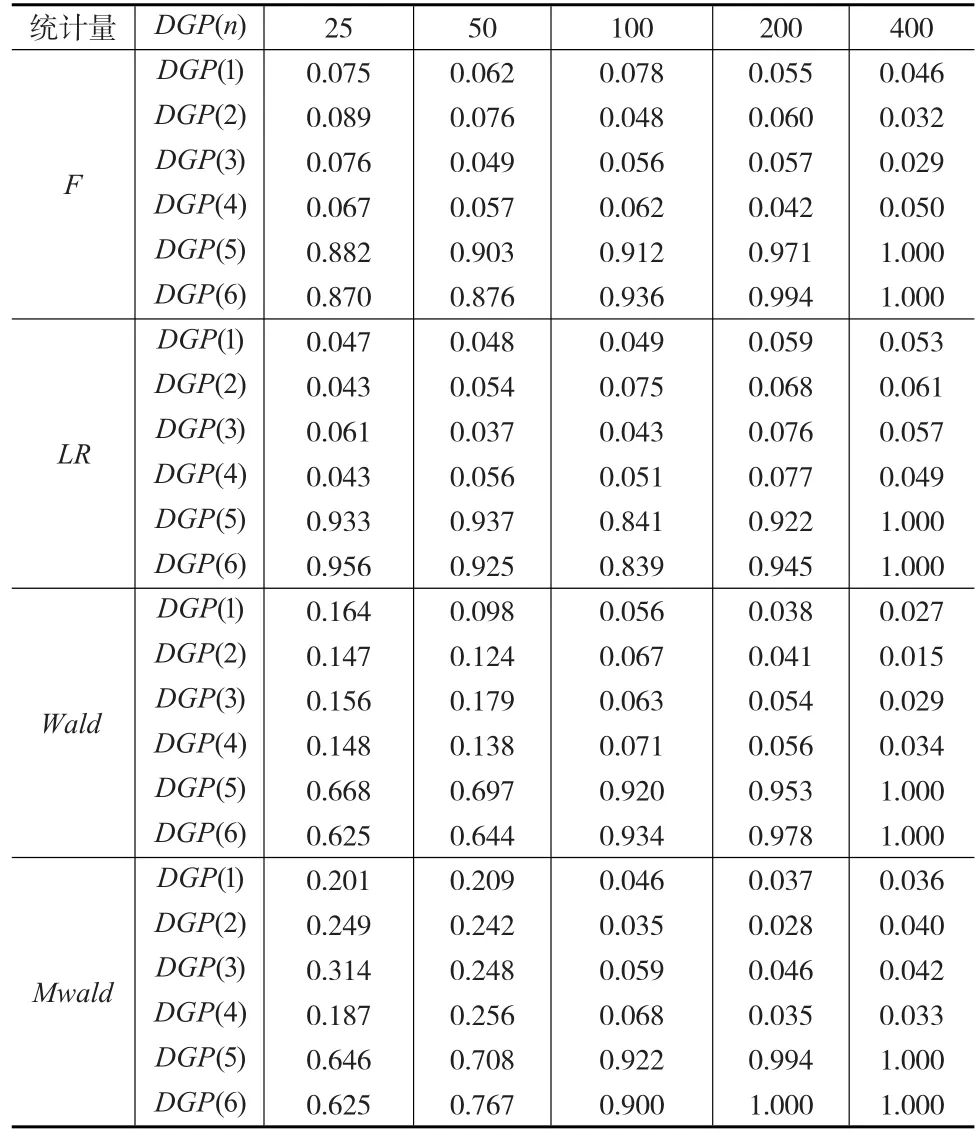
表2 蒙特卡洛模拟下4个统计量的P值

图1 25位样本下四大统计量分布图（二维）

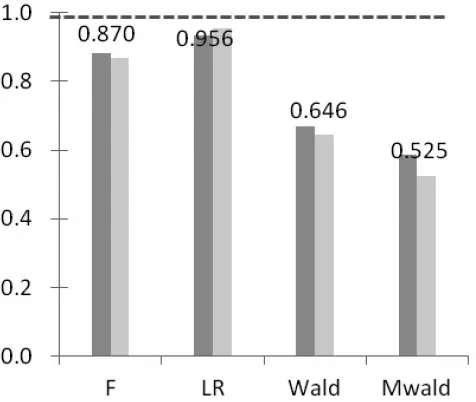
图2 25位样本下四大统计量分布图（三维）

（2）随着样本的增大，Wald、Mwald统计量检验效果逐步改善。考察100位样本的情况，Wald、Mwald统计量在极小样本条件下检验效果差的境况，随着样本的增大而改善。在二维系统中，Wald、Mwald统计量P值相对于25位样本、50位样本中的P值有较大下降。从图3中可以看出，Wald统计量P值在四种数据过程中分别为0.056、0.063、0.071、0.046；Mwald 统计量 P 值在四种数据过程中分别为0.046、0.035、0.059、0.068；Wald 、Mwald统计量P值均位于0.05附近，此时Wald、Mwald统计量均未出现误判，即拒绝了原假设。在三维系统中，Wald、Mwald统计量P值相对于25位样本、50位样本中的P值有较大上升。从图4中可以看出，Wald统计量P值在两种数据过程中分别为0.920、0.934；Mwald统计量P值在两种生成过程中分别为0.922、0.900；Wald、Mwald统计量P值均趋于1，此时Wald、Mwald统计量依然未出现误判，即接受了原假设。这说明样本容量的增大，改善了Wald、Mwald统计量的检验效果。值得注意的是，在100位样本条件下，三维系统中Wald、Mwald统计量的检验效果优于LR统计量。

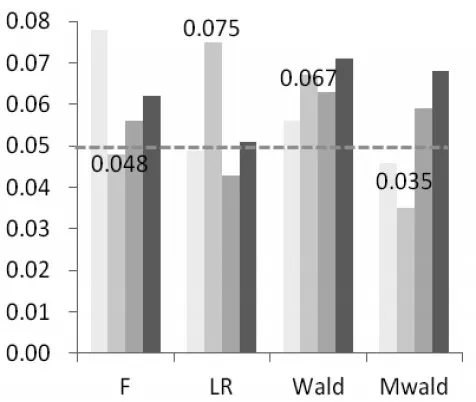
图3 100位样本下四大统计量分布图（二维）

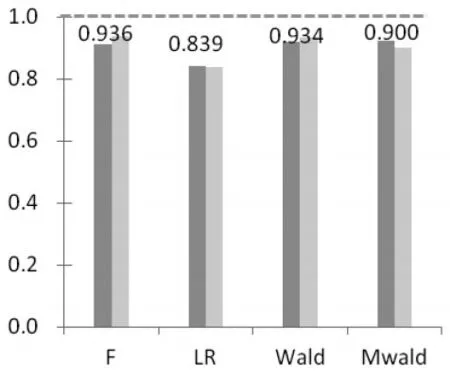
图4 100位样本下四大统计量分布图（三维）

（3）较大样本条件下（n=200，400），F 、LR、Wald、Mwald4个统计量检验效果差异变小，二维系统中Wald、Mwald统计量检验效果最佳，LR统计量检验效果最差。当样本增加到n≥200时，F、LR、Wald、Mwald4个统计量检验效果相差不大。首先观察二维系统，四种数据过程的F、LR、Wald、Mwald统计量平均P值分别为0.039、0.055、0.026、0.033，在0.05显著水平上 F 、LR 、Wald、Mwald基本上都能做出拒绝原假设的判定，并且4个统计量的平均P值相差很小，这说明在较大样本条件下，F、LR、Wald、Mwald在检验格兰杰因果关系时，其检验效果差异变小。三维系统中，两种数据过程的F、LR、Wald、Mwald统计量P值均趋于1，4个统计量都显著地接受了原假设；由此可知，三维系统中F、LR、Wald、Mwald统计量在检验格兰杰因果关系时，检验功效几乎是没有差异的。此外，从图5中可以看出，二维系统中较大样本条件下，Wald、Mwald统计量P值要显著小于LR统计量的P值，此时Wald、Mwald统计量检验效果要优于LR统计量。

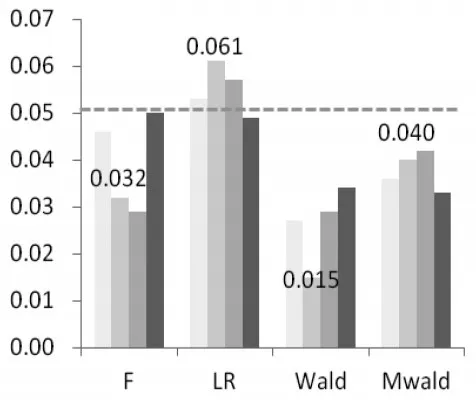
图5 400位样本下四大统计量分布图（二维）

（4）F统计量检验效果比较稳定，不随样本增加出现较大改变。首先考察二维系统，在25、50、100、200、400位样本条件下，F统计量的平均P值分别为0.077、0.061、0.061、0.053、0.039；不管是极小样本还是较大样本，在0.05的显著水平上，F统计量均能做出拒绝原假设的判定，不容易出现误判，说明F统计量检验效果是比较稳定的。同时，当样本量逐渐增加时，F统计量并未出现类似于LR统计量检验效果变差，Wald、Mwald统计量检验效果改善的情况，即F统计量检验效果并不会随着样本容量的增大出现较大改变。三维系统中，在25、50、100、200、400位样本条件下，F统计量的平均P值分别为0.876、0.890、0.924、0.983、1，这说明F统计量在每位样本条件下均显著地接受了原假设，并未出现误判的情况，相对于LR、Wald、Mwald统计量，F统计量在检验格兰杰因果关系时，具有很强的稳定性。从图6中可以看出，在三维系统中，F统计量检验效果同样不随样本增加而出现较大改变。

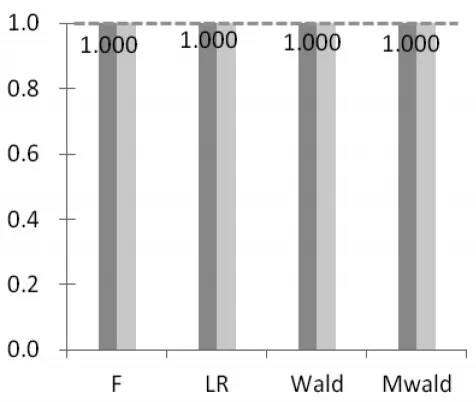
图6 400位样本下四大统计量分布图（三维）

4 结论

在小样本条件下，通过模拟F、LR、Wald、Mwald统计量在检验格兰杰因果关系中的功效，得出以下几点结论：

（1）在极小样本（n≤50）条件下，F 、LR、Wald、Mwald四种统计量中，LR统计量检验效果最佳，Mwald统计量检验效果最差。此时，适合采用LR统计量检验序列间的格兰杰因果关系。

（2）Wald、Mwald统计量检验效果会随着样本容量的增大而得到改善，特别是当样本容量n≥100时，Wald、Mwald统计量几乎不会出现误判的情况；此时，在三维系统中LR统计量检验效果要逊于Wald、Mwald统计量。实际上，当样本容量为100位时，与其他统计量相比，LR统计量检验效果并不理想。

（3）在较大样本（n=200，400）条件下，F 、LR、Wald、Mwald4个统计量的检验效果差异变小，特别是在三维系统中4个统计量的检验效果几乎没有区别；但在二维系统中Wald、Mwald统计量检验效果最佳，LR统计量检验效果最差。在较大样本情况下，适合采用Wald、Mwald统计量检验序列间的格兰杰因果关系。

（4）F统计量检验效果比较稳定，不随样本增加出现较大改变。当样本逐渐增加时，F统计量并不会出现类似于LR统计量检验效果变差，Wald、Mwald统计量检验效果变好的情况。不管是极小样本还是较大样本，F统计量检验格兰杰因果关系的效果都比较稳定。因此，在检验格兰杰因果关系时，F统计量既适用于极小样本，也适用于较大样本。

[1]Granger C W.J.Investigating Causal Relations by Econometric Models and Cross-Spectral Methods[J].Econometrica,1969,（37）.

[2]Sims C A.Money,Income and Causality[J].American Economic Re⁃view,1972,（62）.

[3]Hslao C.Causality Test in in Econometrics[J].Journal of Economic Dynamic and Control,1979b,（4）.

[4]Toda H Y,Phillips C B.The Spurious Effect of Unit Roots on Vector Autoregressions[J].Journal of Econometrics,1993,（59）.

[5]Toda H Y,Yamamoto T.Statistical Inference in Vector Autoregres⁃sions With Possibly Integrated Processes[J].Journal of Econometrics,1995,（66）.

[6]Lütkepohl H.Testing for Nonzero Impulse Response in Vector Autore⁃gressive Processes[J].Journal of Statistical Planning and Inference,1996,（50）.

[7]周建,李子奈.Granger因果关系检验的实用性[J].清华大学学报:自然科学版,2004,（3）.