格兰杰因果关系在复杂网络中的应用*
王芳娟
(浙江师范大学数理与信息工程学院,浙江金华 321004)
0 引 言
格兰杰因果关系在经济、生物、计算神经科学等领域已有广泛的应用.其中,对于二维的时间序列,可以直接用两变量格兰杰因果关系分析数据之间的内在联系.但对于多维的时间序列,用两变量格兰杰因果关系已不能正确判断变量之间的关系是直接的还是间接的,因此提出了条件格兰杰因果关系[1].在实际应用中,若把外部公共输入和隐变量的影响因素考虑在内,则要用到偏相关格兰杰因果关系才能真正刻画变量之间的内在联系[1].
格兰杰因果关系是一种很常用的分析方法,在研究变量之间的因果关系时,通常情况下要求变量的时间序列的长度远远大于变量个数[1-2],此时,格兰杰因果关系法效果显著.但在实际应用中,可以提取到的时间序列长度是有限的,对于数以万计的蛋白质、基因变量,每个变量可以测量到的时间序列长度相当短.此时,变量维数比时间序列长度要大,若仍然用通常的格兰杰因果关系法研究变量之间的内在因果关系,就会得到错误的结论.为了解决这个问题,将提出一种新的方法,在两变量格兰杰因果关系、条件格兰杰因果关系和偏相关格兰杰因果关系的基础上,把简单的格兰杰因果关系应用到复杂网络中.从模拟数据的结果可以看出:该方法能比较有效地揭示复杂网络中变量之间真实的内在联系.
1 预备知识
1.1 线性偏相关格兰杰因果关系
两变量格兰杰因果关系和条件格兰杰因果关系广泛应用于实际数据处理过程中.然而,这2种方法都没有考虑到外部输入和隐变量的影响.如果在实际分析时不将这些因素考虑在内,那么得到的网络结构可能是不正确的.为了更好地处理实际数据中出现的外部输入和隐变量的影响,提出了线性偏相关格兰杰因果关系[1].
考虑2个时间序列Xt和Zt,它们的联合自回归表示为

其中:εit为白噪声;为外部输入;Bi(L为隐变量;i=1,2.
令ui(t)=εit++Bi(L),i=1,2,则误差项协方差矩阵为

若考虑3个变量Xt,Yt和Zt,它们之间的联合自回归模型为


对S,若不考虑u2(t)=的影响,则u1t的方差可以表示为

对Σ,类似地可以考虑去除u5(t)=ε5t+εE5t+B5(L)εL5t的影响,则u3t的方差可以表示为

定义1 Z条件下,Y对X的偏相关格兰杰因果关系为
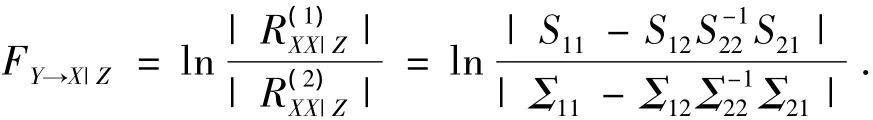
1.2 Bootstrap 方法
Bootstrap法类似重复抽样法,先对原始的数据拟合向量自回归模型[3],利用最小二乘估计法[3]计算其系数矩阵A和误差项方差E;再利用已知条件,构造系数矩阵为A、误差项均值为0、方差为E的多元正态分布白噪声模型,共模拟M(M=500)次,每次计算相应的因果关系或偏相关因果值.其中,3倍的σ(均方差)作为置信区间,若置信区间下限小于0,则表示因果关系不存在,否则,存在因果关系.
2 格兰杰因果关系在复杂网络中的应用
一般情况下,格兰杰因果关系主要用于研究简单的网络结构.在计算过程中,用最小二乘法估计多变量向量自回归模型(MVAR)的参数时,在理论上有一个约束条件,即每个时间序列长度要大于模型中估计的参数个数,对于一个一阶的模型,时间序列长度要大于变量个数的平方[2].但在实际应用中,对于数以万计的蛋白质、基因变量,每个变量可以测量到的时间序列长度相当短.当变量个数超过时间序列长度时,就会出现“维数灾难”,通常的格兰杰因果关系就会失效.为了解决这个问题,提出了一种利用格兰杰因果关系法进行迭代计算的复杂网络研究方法.
2.1 有关概念
在有向网络图中,将对目标节点T有直接或间接作用的所有节点统称为节点T的源节点;并将所有对目标节点T有直接作用的节点统称为节点T的父节点.对任何一个给定的目标节点T,若可以找到所有对它有直接作用的节点(即父节点),则可构造出整个网络.因此,对于给定一个目标节点T,希望找到它所有的父节点.图1(a)表示一个包含目标节点T和它所有源节点的网络.假设{X1,X2,…,Xn}中的每个点到目标节点T只有1条路径,{Y1,Y2,…,Yn}中的每个点到目标节点T有2条不同的路径.图1(b)中通过1条路径连接的间接点都被删除了,剩下的间接点Y1,Y2,…,Yn通过2条不同路径连接.图1(c)中通过1条路径和2条不同路径连接的间接点都被删除了,只剩下目标节点T的父节点T1,T2,T3.

图1 目标节点T的父节点的筛选步骤图
2.2 具体算法
首先,应用两变量格兰杰因果关系,寻找目标节点T的所有源节点,用点集A0(T)表示.在图1(a)中,A0(T)={T1,T2,T3,X1,X2,…,Xn,Y1,Y2,…,Yn}.
其次,进一步检测第1步中找到的连接是直接的还是间接的.执行如下迭代过程[4]:
1)对 A0(T)中的每个节点 a∈{T1,T2,T3,X1,X2,…,Xn,Y1,Y2,…,Yn},计算所有 a→T|b(b∈A0(T),b≠a)的偏相关格兰杰因果关系值.若经计算存在某个b∈A0(T),b≠a,使得a→T|b的偏相关格兰杰因果关系值用Bootstrap法(M=500)计算得到的3δ置信区间下限小于0,则表示a→T的连接是间接的,它们之间不存在直接连接,把a从A0(T)中删除.重复上述步骤,删除所有通过1条路径连接的间接点.图1(a)中,{X1,X2,…,Xn}是通过单一路径连接的间接点集,将其从A0(T)中删除,剩下的点构成一个新的点集,记为 A1(T)={T1,T2,T3,Y1,Y2,…,Yn}.
2)对 A1(T)中的每个节点 a∈{T1,T2,T3,Y1,Y2,…,Yn},按上述方法计算所有 a→T|b,c(b,c∈A1(T),c≠a;b≠c)的偏相关格兰杰因果关系值,其中,b和c的组合共C2n+2种.从而删除通过2条路径连接的间接点.图1(b)中,{Y1,Y2,…,Yn}是通过2条不同路径连接的间接点集,将其从A1(T)中删除,剩下的新点集为 A2(T)={T1,T2,T3}.
3)继续上述步骤,直到不能再从点集Ak(T)中移去任何点为止[4].
2.3 基本原理
若计算得到的两变量格兰杰因果关系值FY→X很大,但在第3个变量Z条件下,偏相关格兰杰因果关系值FY→X|Z显著降低,则表示Y→X的连接是间接的,应删除.利用这个原理,可以寻找每个节点的父节点.
第1阶段,先用两变量格兰杰因果关系法,找出使得Y→X的因果值比较大的所有节点Y,构成候选集A0.
第2阶段,过滤点集A0,保留Y∈A0,满足在任意一个剩余变量Z∈A0,Z≠Y条件下的偏相关格兰杰因果关系值FY→X|Z都很大,得到剩余点集A1.
第3阶段,利用新点集A1,再次过滤点集A1,保留Y∈A1,满足在任意2个剩余变量Z1,Z2∈A0(Z1,Z2≠Y;Z1≠Z2)条件下的偏相关格兰杰因果关系值FY→X|Z1,Z2都很大,得到剩余点集A2.
第4阶段,再利用点集A2,以其中任意3个不同剩余变量为条件,继续上述步骤,直到这种迭代进行不下去为止.
通过上述迭代步骤,将格兰杰因果关系法应用到复杂网络中,使得每个节点对应一列父节点,就可以得到复杂网络的因果关系图.
3 数值模拟
下面验证本文方法在复杂网络中应用的有效性(能否用格兰杰因果关系法正确刻画长度有限的多变量之间的因果关系).首先,利用一个模拟的例子(由12个时间序列组成)来进一步说明.其次,利用例子拟合的多维数据,将本文的新方法和简单网络中的偏相关格兰杰因果关系法的计算结果进行比较.
例1 假设12个变量的时间序列由如下的动力方程确定:
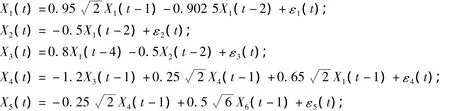

其中,εi(i=1,2,…,12)是相互独立、均值为0、方差为1的白噪声.由这个模型直接可得12个变量之间的因果关系,如图2(b)所示,共有18条连接边.取模型中每个变量的200个时间点作为拟合数据,所得数据轨迹如图2(a)所示.为了增加可视性,将X1,X2,…,X12进行了平移,依次从下到上排列.

图2 数据的轨迹及相应的网络结构
利用上述方法研究该拟合数据的网络结构.先对数据计算两变量格兰杰因果关系值,用Bootstrap法得到的连接图如图3(a)所示,共有95条连接边,比真实的网络多出很多边,原因是两变量格兰杰因果关系不能区分连接是直接的还是间接的,在其中混杂了许多间接连接的边.
接着,按上述迭代步骤,依次计算1个、2个变量条件下的偏相关格兰杰因果关系值,分别用于除去通过1条、2条路径连接的间接点,用Bootstrap法后所得的结果如图3(b)和(c)所示,分别有19条和18条边.它们和图3(a)相比已经去掉了很大一部分间接连接边,比较接近真实结构.说明该模拟数据利用上述迭代步骤可以比较正确地判别出网络结构.
最后,作为比较,对12个变量两两之间直接计算偏相关格兰杰因果关系值(对研究的2个变量,以其他剩余的所有变量为条件),用Bootstrap法后所得的网络结构如图3(d)所示,与真实的网络结构相比缺少一些连接边.该方法所得结果和真实结构相比误差比较大.这是由于模型的阶为4,在模型中要估计的参数总数是12×12×4=576,而已有的时间序列长度只有200,不足以用它来估计所有参数,导致计算得到错误的因果连接.
图3(A),(B),(C),(D)表示网络图 3(a),(b),(c),(d)的关系图.若某种关系(行指标表示原因,列指标表示结果)经Bootstrap法得到的置信区间下限小于0,则为黑色,表示变量之间没有因果关系;若下限大于0,则为白色,表示变量之间有因果关系存在.
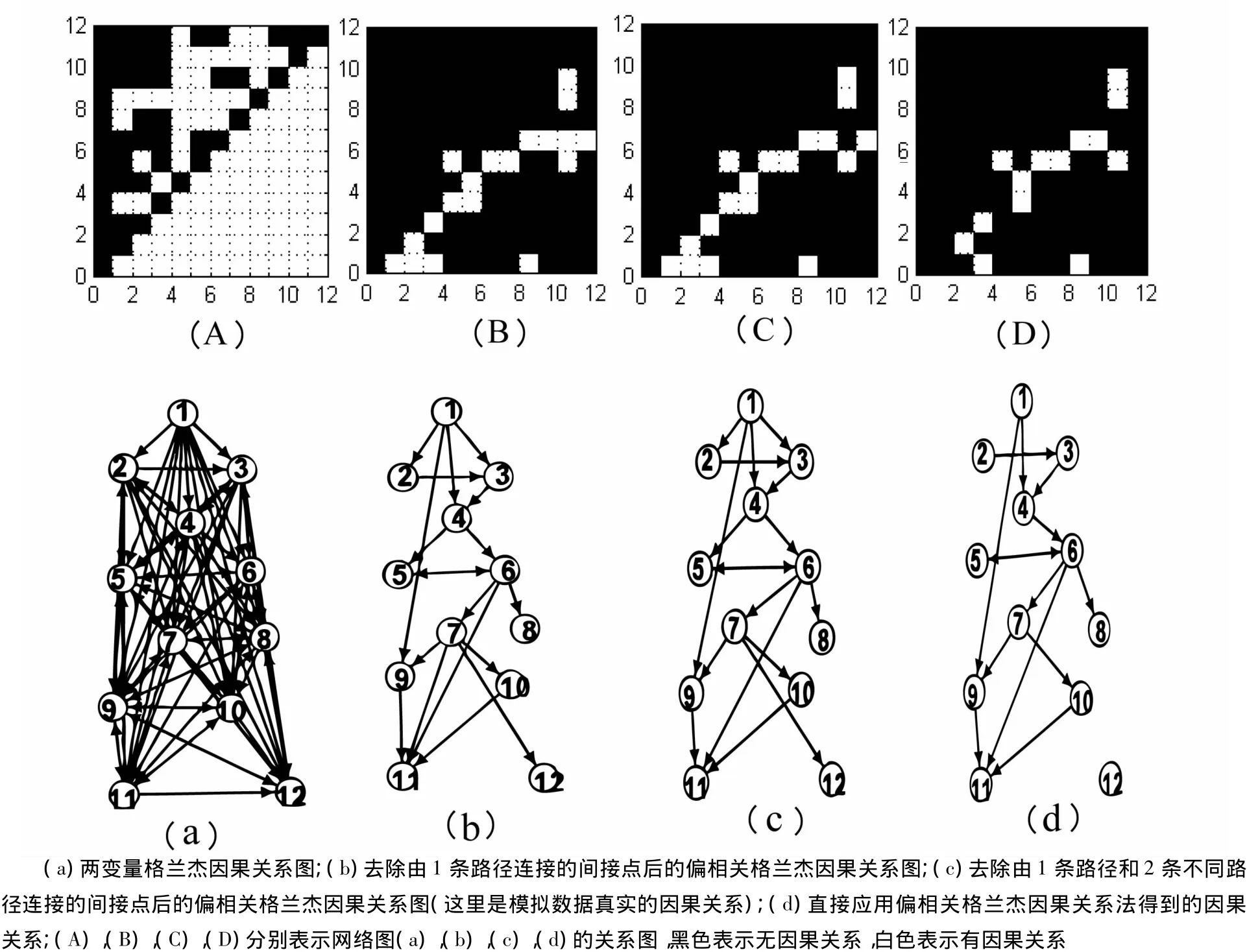
图3 不同方法所得的网络结构图
4 结 语
在实际应用中,研究的网络通常是多变量复杂网络,此时直接应用偏相关格兰杰因果关系得到的结果往往是不稳定的,与真实的网络结构存在很大偏差.为了解决“维数灾难”这个难题,把格兰杰因果关系法应用到复杂网络中,基于两变量格兰杰因果关系、条件格兰杰因果关系、偏相关格兰杰因果关系,用迭代法一步步除去通过1条单一路径、2条不同路径等的间接连接,直至除去所有间接连接.最后剩下每个节点的父节点,从而构造出相应复杂网络的结构.格兰杰因果关系在复杂网络中的迭代应用是对通常格兰杰因果关系的优化,弥补了其对维数限制的不足.该方法对今后利用格兰杰因果关系法研究其他各种复杂网络结构有很大的帮助.
[1]Guo Shuixia,Seth A K,Kendriek K M,et al.Partial granger causality-eliminating exogenous inputs and latent variables[J].Journal of Neuroscience Methods,2008,172(1):79-93.
[2]Gopikrishna D,Stephan L C,George A J,et al.Multivariate granger causality analysis of fMRI data[J].Human Brain Mapping,2009,30(4):1361-1373.
[3]何书元.应用时间序列分析[M].北京:北京大学出版社,2003:300-305.
[4]Zou Cunlu,Christophe L,Guo Shuixia,et al.Identifying interactions in the time and frequency domains in local and global networks:A granger causality approach[J].BMC Bioinformatics,2010,11:337-341.

