正态云线性回归模型及其最小二乘参数估计方法

龚艳冰，戴靓靓，刘高峰

（河海大学 企业管理学院，江苏 常州 213022）

0 引言

在预测评价与决策等领域，回归分析方法是一个重要且常用的研究方法，但是传统回归往往依赖于精确的统计数值及二值逻辑。在社会经济活动中，部分或者全部的观测数据常常是不精确或者用语言值描述的数据，使得经典线性回归模型受到限制。人们常常使用自然语言值表示定性概念，例如大概、温度不高、相当小等，恰恰是人们赖以识别分析乃至决策的重要依据。现实世界中不确定性主要包括随机性和模糊性，当观测变量的不确定性不是由概率分布给出的，而是由隶属函数确定的，相应的回归模型称为模糊线性回归模型。模糊线性回归模型由日本学者Tanaka等人[1]首次提出的，主要用于反映自变量和因变量的模糊关系。经典回归模型把真实数据和估计值之间的偏差认为是观测误差，而模糊回归模型将这种误差视为系统结构自身的模糊性，并把数据和其估计值之间的偏差视为系统参数的模糊性，从而由参数模糊化来解决这一问题。国内外许多学者对模糊回归模型的参数估计方法进行了大量研究[2-7]，并在系统预测、评估和决策等方面进行了大量应用研究[8-10]。

随机性和模糊性是不确定性问题中的两个基本特征，经典的线性回归模型和模糊回归模型分别对这两种不确定性进行了研究，但是两种之间的关联性研究一直没有引起人们足够的重视，即同时考虑随机性和模糊性。为了处理定性概念中广泛存在的随机性和模糊性，李德毅等[11]首次提出云模型，利用二阶的高斯分布方法，来反映定性概念的随机性，同时又通过计算求得反映定性概念的模糊性。本文在云模型理论的基础上，考虑不确定性回归中模糊性和随机性的关联性，将传统的线性回归模型进行拓展和推广，提出正态云线性回归模型并对参数进行估计。最后给出一个人员绩效评估的应用实例，说明模型的有效性。

1 云模型基本理论

云模型反映了随机性和模糊性之间的关联，借助高斯概率密度分布函数，通过构造二阶或者高阶的云发生器形成偏离高斯分布的云滴群，用概率的方法去研究模糊性[11]。经过几年的发展和完善，目前云模型已成功应用于智能控制、数据挖掘、预测和评估等领域[12-14]。云模型是用语言值表示的某个定性概念与其定量表示之间的不确定性转换模型，它把模糊性与随机性这二者完全集成在一起构成定性和定量相互间的映射。

定义1：设A是论域U上的定性概念，若定量值x∈U，且x是定性概念A的一次随机实现，若满足：x～N（Ex，En′2），其中，N（En，He2）且对A的确定度满足：

则称在论域U上的分布成为正态云模型。

正态云模型具有普适性[15]，是基本的云模型。正态分布大量社会和自然科学中定性知识的云的期望曲线都近似服从正态或半正态分布。正态云的数字特征反映了定性概念和定量特性，用期望Ex（Expected Value）、熵En（Entropy）、超熵He（Hyper Entropy）三个数值来表征。由统计学3En规则可知，当0＜He＜En/3时，99.7%的云滴落在外包络曲线[11]：

和内包络曲线：

图1 正态云和包络曲线

之间的区域内，如图1所示。对于任意给定的确定度μ=α（0＜α＜1），正态云A与包络曲线相交得到二个区间分别为：定义2：假设在同一论域U中，存在n个正态云模型Ai=（Exi,Eni,Hei）和系数ki∈R，则合成云As=（Exs,Ens,Hes）可以定义如下：

定义3：假设两个正态云A和B，对于给定的确定度μ=α（0＜α＜1），则正态云A和B之间的包络距离定义为：

特别的，取α=k/m（k=1,…,m）可得正态云A和B之间的离散化包络距离为：

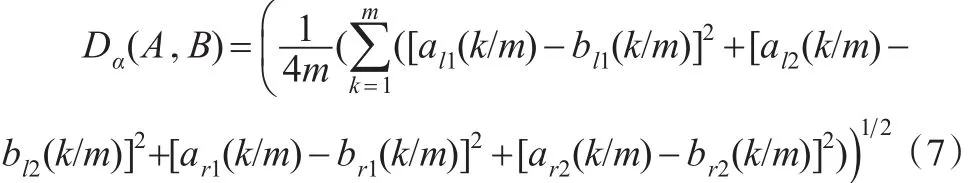
容易验证，式（6）和式（7）具有非负性、对称性且满足三角不等式，因此，D（A，B）是距离测度。包络距离的基本思想是两个定性概念相似，只需要它们的包络相似，允许包络内部存在小的差异，这种差异反映了概念的模糊性和随机性，这也符合人们的思维认识。

2 正态云线性回归模型及其参数估计

2.1 正态云线性回归模型

考虑自变量和因变量都具有模糊随机性质的线性回归模型，即：

其中，xi= （1,x1i,x2i,…,xpi）表示正态云自变量向量，yi表示正态云因变量，aj,j=0,1,2,…,p为回归系数估计值。为方便起见，可令正态云xji=（Exji,Enji,Heji）（j=0,1,2,…,p;i=1,2,…,n），则式（8）的正态云数据回归模型可改写成：

由概率统计知识可知，p个相互独立的服从正态分布的随机变量xji（j=1,2,…p;i=1,2,…,n）满足xji～N（Exji，则其线性组合a0+a1x1i+a2x2i+…+apxpi仍然是一个正态分布，即因变量 y（xi）满足其中因此，正态云线性回归模型（9）的因变量y（xi）也是一个正态云。

特别的，如果对正态云自变量xji=（Exji,Enji,Heji）中所有的i,j有Heji=0，则模型（9）就退化为正态模糊线性回归模型，如果对所有的i,j有Enji=Heji=0，则模型（9）就退化为传统的线性回归模型，因此，云模型是经典线性回归模型和模糊线性回归模型的一般形式。

由合成云的定义（5）可得正态云线性回归模型y（xi）的合成云模型为：对于给定的确定度μ=α（0＜α＜1），由图1可知正态云变量是直线μ=α上的两个线段上的不确定性变量，只需要保证不超出包络曲线的范围。因此，在给定确定度α下，只需要保证回归模型的包络曲线相等，即模型（9）可以转化为四个传统回归模型：

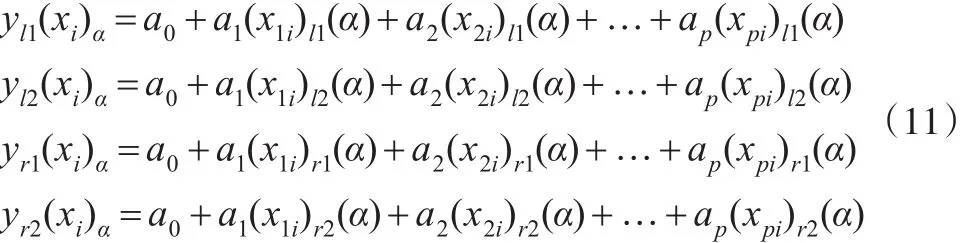
2.2 模型的参数估计

结合正态云离散包络距离的定义（7），可将正态云因变量估计值与观测值间的均方误差表示为：

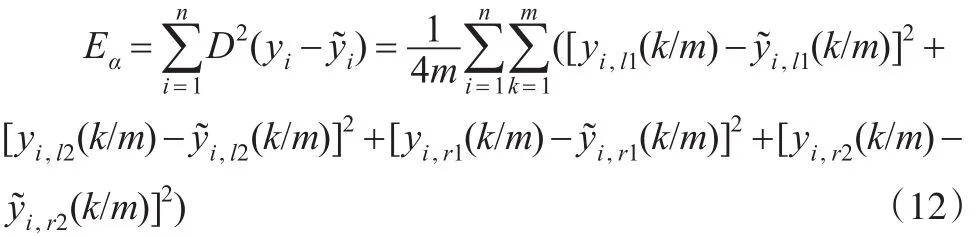
将式（12）代入式（7）可得均方误差为：

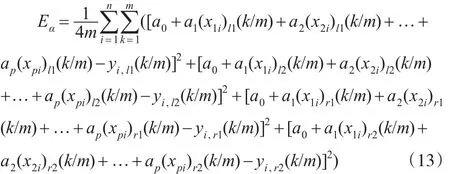
根据最小二乘法令：

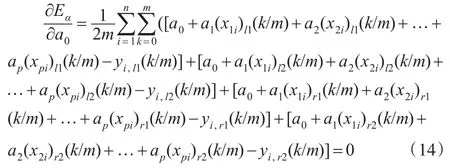
和

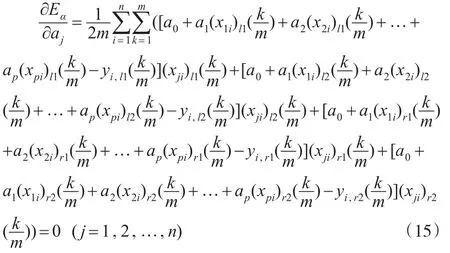
通过求解上述线性方程组（14）和（15）可得到正态云线性回归模型（9）的回归系数的估计值，我们称这种基于离散距离的最小二乘参数估计方法为云最小二乘方法（CLS）。

为了有效评估正态云线性回归模型的性能，需要对模型的误差进行估计。传统的回归分析是针对观测值与拟合值的距离进行比较，利用点对点的差距来评价拟合结果，而正态云拟合则关心的是实际的云滴与估计的云滴的差距，因此无法用衡量传统回归分析拟合效果的方法加以分析。为此，本文将拟合值与实际值之间的离散距离差E=作为误差估计的检验依据，当回归方程拟合出来的正态云模型具有较小的E值，即包络曲线越接近则内部的云滴之间的差距就越小，说明该模型应该是不错的模型。为方便起见，可以考虑合成云ysi与实际值yi之间的离散距离差作为误差估计的检验依据。

3 正态云回归方法应用

为了说明本文方法的可行性，以Chen等[2]给出的人员绩效评估的例子进行实证研究。人员绩效评估是企业人力资源管理中一项重要的功能，显然，由于人员绩效评估的主观性，通常采用语言值来描述评估值，语言值是一个模糊性和随机性共存的不确定因素，科学合理的评估结果将影响到人力资源管理功能的整体表现。根据人力资源管理的相关理论，考虑工作绩效（因变量y）的四个主要影响因素（自变量）包括[2]：工作能力（x1）、抗压性（x2）、拖延频率（x3）和沟通和协调能力（x4），样本容量为30。显然这四个因素数据本身同时具有模糊性和随机性，假定影响因素评估论域均为[0，100]。首先按照正态云数据生成方法，即：

将30个模糊样本生成正态云数据，如表1所示。

表1 绩效评估自变量和因变量正态云样本

应用Matlab软件，将上述数据代入线性方程组（14）和（15）可得下列线性方程组：

120a0+80400 a1+81200 a2+73280 a3+61720 a4=63640

80400 a0+5754424.4 a1+5442693 a2+4854687.7 a3+4067925.8 a4=4591220

81200 a0+5442693 a1+5.746256.8 a2+5.142517.4 a3+4.250704.6 a4=425566.5

73280 a0+4854687.7a1+5142517.4 a2+4.991726.3 a3+3716504.2 a4=3738481.6

61720 a0+4067925.91a1+4250704.6 a2+3716504.2 a3+3766932.8 a4=3277507.7

求解上述线性方程组，可得回归系数：

a0=-0.1290，a1=0.9237，a2=-0.1289，a3=-0.1120，a4=0.1305

则正态云线性回归方程为：

y（xi）=-0.1290（1,0,0）+0.9237（Ex1i,En1i,He1i）-0.1289（Ex2i,En2i,He2i）-0.1120（Ex3i,En3i,He3i）+0.1305（Ex3i,En3i,He3i）

从上述回归模型看到工作能力（x1）对员工工作绩效的影响是最大的，沟通和协调能力（x4）对员工工作绩效也存在正面影响，弱抗压性（x2）和拖延频率（x3）这两个变量对工作绩效产生负面影响但影响力度不大，这与实际情况是相一致的。为方便起见，本文以合成云（ys）表示正态云线性回归的拟合值，图2给出了样本x1=（x11,x12,x13,x14）的正态云线性回归拟合示意图。

图2 正态云线性回归拟合示意图

选取确定度α=0.1,0.2,…,1，计算合成云ysi与实际值yi之间的离散包络距离差并将其作为误差估计的检验依据，结果如表2所示。结果表明，本文的正态云线性回归模型是可行的，而且与传统线性回归模型和模糊线性回归模型比较误差也相对较小，最主要的是正态云线性回归模型的适应性更强，是更加一般和灵活的线性回归模型。

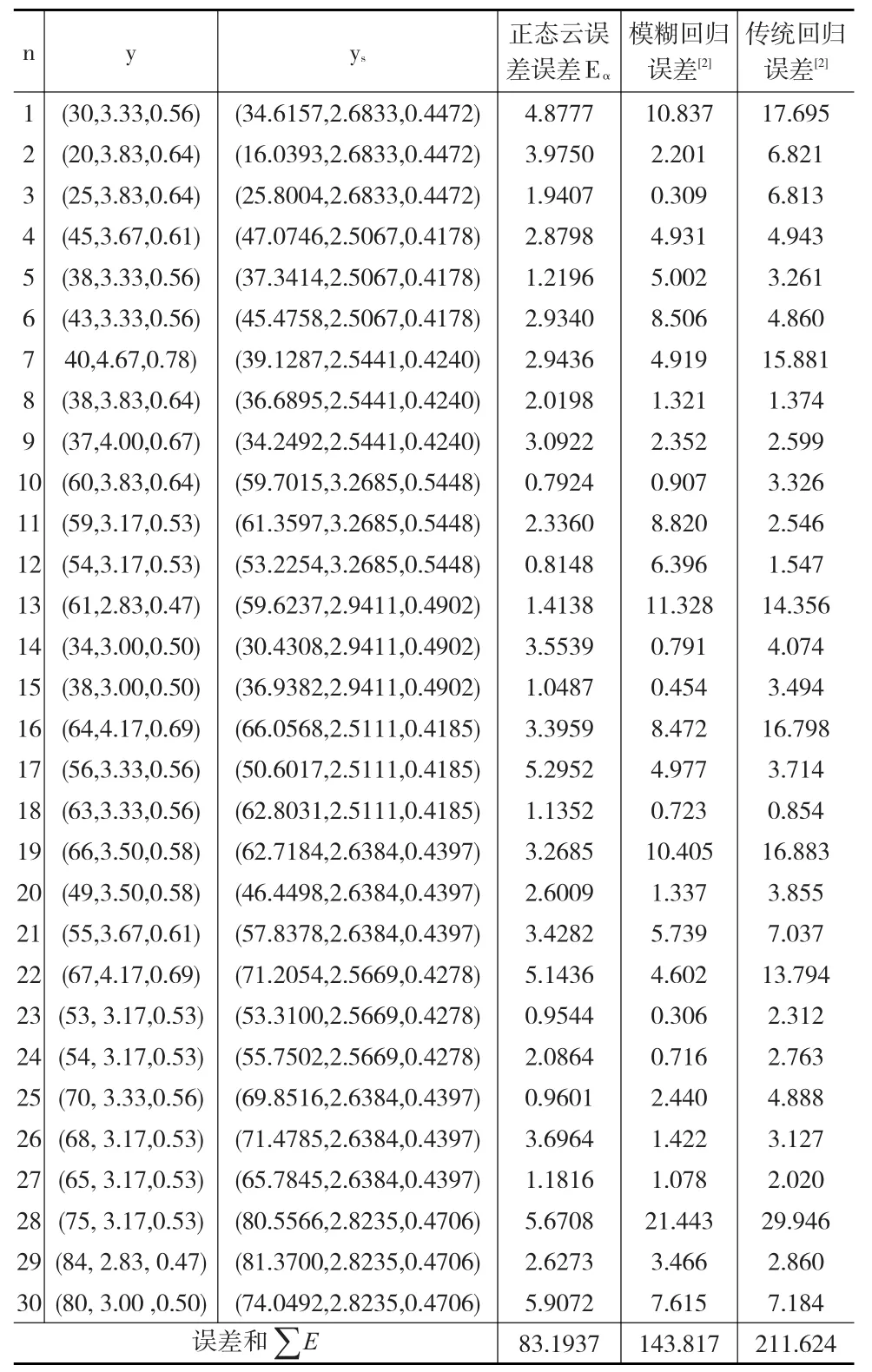
表2 正态云拟合效果与距离误差测度表

4 结论

云模型方法指出，客观上人们在不确定性思维中，也许并不存在一个确定又精确的隶属度或者隶属函数。因此，模糊线性回归模型虽然在处理不确定性回归分析中较传统回归模型取得了较好的效果，但是确定而又精确的隶属度方法容易把人们对模糊现象的处理强行纳入精确数学的领域，扼杀了事物的高阶模糊本质[11]。为此，本文将云模型方法应用于不确定问题的线性回归分析领域，提出正态云线性回归模型，并基于最小二乘的思想给出最小二乘包络距离方法对正态云回归模型的系数进行估计。正态云线性回归模型的优点包括：①是传统回归模型和模糊回归模型的推广；②将数据和其估计值之间的偏差视为系统参数的模糊性和随机性关联产生的结果；③通过正态云的三个数字特征可以反映回归模型的不确定性程度，更加符合自然语言值的内涵。

[1]Tanaka H,Uejima S,Asai K.Linear Regression Analysis With Fuzzy Model[J],IEEETransactionsonSystemsMan,andCybernetics,1982,（12）.

[2]Chen L H,Hsueh C C.Fuzzy Regression Models Using the Least-squares Method Based on the Concept of Distance[J].IEEE Transactions on Fuzzy Systems,2009,（17）.

[3]Farhadinia B.Sensitivity Analysis in Interval-valued Trapezoidal Fuzzy Number Linear Programming Problems[J].Applied Mathemati⁃cal Modelling,2014,（38）.

[4]Wan S P,Dong J Y.Possibility Linear Programming With Trapezoidal Fuzzy Numbers[J].Applied Mathematical Modelling,2014，（38）.

[5]Ebrahimnejad A,Tavana M.A Novel Method for Solving Linear Pro⁃gramming Problems With Symmetric Trapezoidal Fuzzy Numbers[J].Applied Mathematical Modelling,2014,（38）.

[6]任燕,郭嗣琮.基于结构元最小二乘序的模糊线性回归[J].模糊系统与数学,2015,29（1）.

[7]李俊红,曾文艺.基于梯形模糊数的模糊最小一乘回归模型[J].系统工程理论与实践,2015,35（6）.

[8]柏林,房勇.基于模糊回归分析的投资组合选择模型[J].系统工程理论与实践,2015,35（7）.

[9]张转,常安定,王媛英,王晓晨.基于正态模糊线性回归确定河流横向扩散系数[J].长江科学院院报,2015,32（8）.

[10]邵良杉,赵琳琳,温廷新,孔祥博.基于模糊多元线性回归模型的岩石可爆性评价[J].中国安全科学学报,2015,25（7）.

[11]李德毅,杜鹢.不确定性人工智能（第二版）[M].北京:国防工业出版社,2014.

[12]Li D Y,Liu C Y,Gan W Y.A New Cognitive Model:Cloud Model[J].International Journal of Intelligent Systems,2009,（24）.

[13]龚艳冰,张继国.基于正态云模型和熵权的人口发展现代化程度综合评价[J].中国人口·资源与环境,2012,（1）.

[14]龚艳冰,刘高峰,冯兰萍,张继国,胡娜.江苏省水资源短缺风险的相似云评价方法研究[J].长江流域资源与环境,2015,（6）.

[15]李德毅,刘常昱.论正态云模型的普适性[J].中国工程科学,2004,6（8）.