数列与不等式

■郑州外国语学校 王艳丽

(一)数列

1.等差与等比数列的概念、通项公式。

等差数列 等比数列=q an+1-an=d an+1 an定义an+2-an+1=an+1-an an+2 an+1=an+1 an通项公式 an=a1+(n-1)d an=a1qn-1 an=am+(n-m)d an=amqn-m

2.合理选用等差、等比数列的求和公式。

3.常用性质。

(1)在等差数列{an}中,若自然数m、n、p、q满足:m+n=p+q(m、n、p、q都是正整数),则am+an=ap+aq。

类比:在等比数列bn{}中,若自然数m、n、p、q满 足:m+n=p+q(m、n、p、q都 是 正整数),则bnbm=bpbq。

(2)若{an}是等差数列,Sn为前n项和,列。

类比:若{bn}是等比数列,Tn为前n项积,则 {}是以b1为首项、q为公比的等比数列。

(3)等差数列{an}的前n项和为Sn,则Sm,S2m-Sm,S3m-S2m,S4m-S3m,…仍构成等差数列,公差为m2d。特别地,S3m=3(S2m-Sm)。

(二)不等式

1.均值不等式拓展。

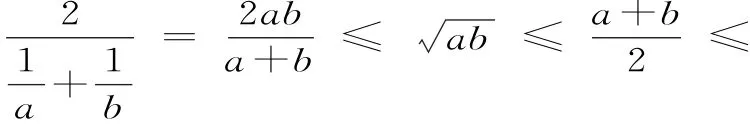
2.柯西不等式。

向量形式:|a||b|≥|a·b|;特殊形式:(a2+b2)(c2+d2)≥(ac+bd)2。

3.平面三角不等式。

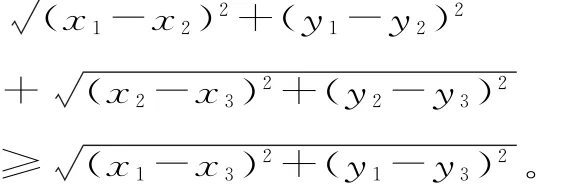
4.贝努利不等式。

(1+x)n＞1+nx,(x＞-1,x≠0,n为大于1的正整数)。

5.排序不等式。

“逆序和≤乱序和≤顺序和”,即设a1≤a2≤…≤an,b1≤b2≤…≤bn为两组实数,c1,c2,…,cn是b1,b2,…,bn的任一排列,则a1bn+a2bn-1+…+anb1≤a1c1+a2c2+…+ancn≤a1b1+a2b2+…+anbn,当且仅当a1=a2=…=an或b1=b2=…=bn时,逆序和等于顺序和。

1.若数列{an}的前n项和Sn=an-2n,求an。

审题方法:先求出a1,再求an(n≥2),验证n=1时是否适合an。

解题思路:(1)当a=0时,Sn=-2n。

若n≥2,an=Sn-Sn-1=-2n-(-2n-1)=-2n-1。

若n=1,a1=S1=-2,不适合an=-2n-1。

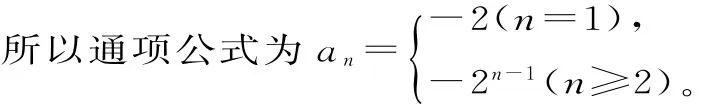
(2)当a≠0时,an=(a-1)an-1-2n-1(请读者自己完成)。

多解多变:为什么a=0时,an=Sn-Sn-1=-2n-1不是通项公式?为什么a≠0时,an=Sn-Sn-1=(a-1)an-1-2n-1就是通项公式呢?an=Sn-Sn-1对n=1也成立的充要条件是什么?

当n=1时,a1=S1-S0,又a1=S1,所以S0=0。因此,an=Sn-Sn-1对n=1也成立的充要条件是S0=0。

于是,我们总结出了能否直接用“an=Sn-Sn-1”求通项公式的判别方法:

①当S0=0时,an=Sn-Sn-1;

2.在数列 an{}中,a1=1,an=3an-1+2(n≥2,且n∈N*),求通项公式an。

审题方法:考虑如何将不规范的式子化为规范的式子,将式子变为等差或等比数列的基本形式,可以尝试待定系数法、换元法,两边除以某个数的n次方,求出新数列的通项公式,进一步即可求解。

解题思路:设an+k=3(an-1+k),则an=3an-1+2k,于是2k=2,可得k=1,因此an+1=3(an-1+1),故{an+1}是以a1+1=2为首项,3为公比的等比数列。

所以an+1=2·3n-1,即an=2·3n-1-1(n ∈N*)。

多解多变:(换元法)由已知递推式可得

①-②得an+1-an=3(an-an-1),设b=a-a,则

因此数列{bn}是首项为b1=a2-a1=5-1=4,公比为3的等比数列。

又bn=an+1-an=4×3n-1,故an=2·3n-1-1(n ∈N*)。

因此an=2·3n-1-1(n ∈N*)。