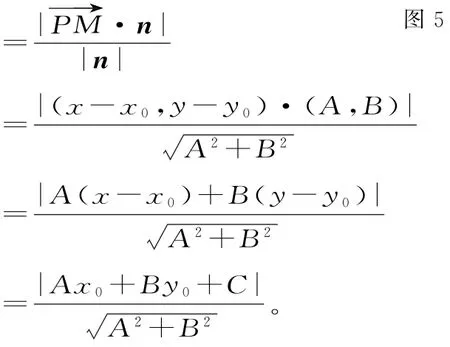三角函数与平面向量

■郑州外国语学校 曹四清(正高级教师)

编者的话:基本知识和基本技能是高中数学的核心,同学们一定要高度重视。本期特约郑州外国语中学曹四清等几位老师为同学们解读相关知识。郑州外国语中学是河南省名牌高中,多年来高考成绩一直在全省名列前茅。愿同学们通过阅读,能从中感悟知识的结构与拓展,把握高考命题特点与趋势。

1.关于特殊角的三角函数。

熟练掌握0°,30°,45°,60°,90°的特殊三角函数值;较高要求:了解15°,18°及其倍数的三角函数值。

2.同角三角函数间的关系。

同角三角函数有常用的三种基本关系:倒数关系、平方关系与乘积关系。

倒数关系:如图1,对角的两个三角函数值的乘积为1。(1)sinα·cscα=1;(2)cosα·secα=1;(3)tanα·cotα=1。

平方关系:如图1,在阴影三角形中,上面两个顶点处的三角函数值的平方和等于下面顶点处的三角函数值的平方。sin2α+cos2α=1,1+tan2α=sec2α,1+cot2α=csc2α。

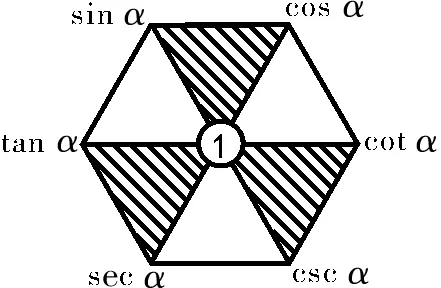
图1

乘积关系(商数关系):(1)如图1,六边形任意顶点上的函数值等于与它相邻的两个顶点处函数值的乘积。sinα=cosα·tanα,cosα=sinα·cotα,cotα=cosα·cscα。(2)如图1,六边形任意顶点上的函数值等于与它相邻的顶点处与次相邻的顶点处函数值的商。

(2)三角函数值的给出一般有两种情况。(1)给出一个具体值(根据此值来确定所讨论的象限);②给出一个未知的常数(根据平方关系确定要讨论的象限)。

(3)任意给出一个三角函数值,都可以求出其他的五个三角函数值。已知sinα=a(a≠0,±1),试求

α的其他五个三角函数值。

3.弧长与扇形面积公式。

4.诱导公式。

口诀:“奇变偶不变,符号看象限,α当作锐角看”。

5.三角函数的图像与性质。

(1)图像的变换。

三角函数的变换方式有六条路径。y=Asin(ωx+φ),其中参数有A,ω,φ,变换的种类数就是其排列数,有=6(种)。

(2)图像的性质。

复习函数的性质要从定义域、值域、函数关系、特殊点、对称性(奇偶性)、单调性、周期性等方面进行归纳总结。

图2

1.两向量共线。

(1)b≠0,若a∥b,则存在实数λ,使得a=λb。

(2)坐标表示:a=(x1,y1),b=(x2,y2),a∥b⇒x1y2-x2y1=0。

2.两向量垂直。

(1)向量a,b,若a⊥b⇒a·b=0。

(2)坐标表示:a=(x1,y1),b=(x2,y2),a⊥b⇒x1x2-y1y2=0。

3.平面向量基本定理。

图3

4.向量的数量积满足结合律吗?

实数乘法结合律:(xy)z=x(yz)。分别用一个、两个、三个向量去代替式中的x、y、z便可得到:实数与向量的积满足结合律:λ(μa)=(λμ)a,内积满足结合律:(λa)·b=λ(a·b)=a·(λb),同时得到了三个向量的结合式:(a·b)c=(b·c)a,此式记作(*)式,显然它不一定成立。那么,何时它成立呢?

当a=0或b=0或c=0时,式子显然成立。

当a≠0且b≠0且c≠0时:

(1)若a、c不共线,则:

①a·b≠b·c,显然不成立;

②a·b=b·c≠0,显然不成立;

③a·b=b·c=0,则有b⊥a,b⊥c,则a∥c,矛盾。

可知,a、c不共线时不成立。

(2)若a、c共线,则由共线向量定理,得a=λc(λ∈R),所以(a·b)c=(λc·b)c=λ(b·c)c=(b·c)(λc)=(b·c)a,从而(a·b)c=(b·c)a成立。

综上,a、b、c至少一个为0或a∥c时,(*)式成立,反之不成立。

在向量研究中,每个向量式都对应了一个坐标式,用坐标法研究上式如下:

设a=(x1,y1),b=(x2,y2),c=(x3,y3),则(a·b)c=(x1x2+y1y2)(x3,y3)=(x1x2x3+y1y2x3,x1x2y3+y1y2y3),(b·c)a=(x2x3+y2y3)(x1,y1)=(x1x2x3+x1y2y3,x2x3y1+y1y2y3)。

由(a·b)c=(b·c)a,即(x1x2x3+y1y2x3,x1x2y3+y1y2y3)=(x1x2x3+x1y2y3,x2x3y1+y1y2y3),所以

论与用向量运算得出的结论是一致的。

5.为什么要学习投影?

图4

(推导点到直线的距离公式)已知P(x0,y0)和直线l:Ax+By+C=0(A、B不全为0),求证:点P到直线l的距离为

证明:n=(A,B)是l的一个法向量,M(x,y)是l上任意一点,如图5。

图5