改进的模糊粗糙集模型

陶 志，潘丽平，何丹峰

（中国民航大学理学院，天津 300300）

改进的模糊粗糙集模型

陶 志，潘丽平，何丹峰

（中国民航大学理学院，天津 300300）

模糊粗糙集模型是对经典粗糙集模型的扩充，然而却有其不足之处。本研究提出的改进的模糊粗糙集模型，是建立在一般模糊粗糙集模型基础之上，将一个论域扩充成两个论域，同时重新定义了模糊粗糙集合的隶属函数，从而有效提高了新模型的粗糙近似精度和应用范围。理论分析和实例计算均证明了新模型的有效性和实用性。

粗糙集；模糊集；模糊关系；模糊粗糙集模型

?

粗糙集理论[1]是1982年由波兰数学家Pawlak提出的[2]。该理论作为一种数学工具用来处理不完整和不确定性知识，现已广泛应用于人工智能、模式识别与分类、知识发现、决策支持系统、数据挖掘和专家系统等领域。

模糊集理论[3]是由美国控制论专家Zadeh在1965年提出的，该理论也是一种用来处理模糊和不确定性知识的数学工具。粗糙集理论和模糊集理论均可用来处理模糊和不确定性问题，并且这两种理论在处理问题时具有一定的相似性。因此，把他们结合起来研究模糊和不确定性问题更具有实用价值。

Pawlak粗糙集模型是由论域U、U上的二元等价关系R以及被近似描述的集合X这3个最基本的要素所构成。因此，经典粗糙集模型的扩充形式也主要有3个方向，即从论域方向、从关系方向和从被描述的概念方向。

在用粗糙集知识进行属性约简之前，首先要将连续属性离散化。在此过程中，将会引起信息在某种程度上的损失。为了解决这种信息损失问题，法国学者Dubois等[4]将模糊集理论引入到粗糙集中，提出了模糊粗糙集理论。该理论在进行属性约简时对信息系统中的对象不再进行离散化，并且在讨论对象间的相互关系时用到了相似关系而非粗糙集中的等价关系。此后，也有学者在Pawlak经典粗糙集模型的基础上把等价关系换成模糊关系，被近似对象换成模糊集合，提出新的模糊粗糙集模型[5]。然而，该模型仅仅限于对同一论域中的模糊集进行近似描述，并且近似精度也不够高。

目前，基于双论域的粗糙集理论引起了越来越多的学者关注[6-8]，本文就是在文献[5]所给的一般模糊粗糙集模型的基础上把一个论域扩充为两个论域，同时给出了在双论域中模糊近似算子隶属函数的定义，从而得到一种改进的模糊粗糙集模型。把一个论域U推广为两个论域U、V，即把模糊关系⊆U×U推广为一般模糊关系⊆U×V，其特点是论域U中模糊集B的下、上近似是由另一个论域V中的一对模糊集来表达的，因此应用范围更加广泛。此外，由于本文引进了新的模糊近似算子隶属函数的定义，使得改进的模糊粗糙集模型比一般模糊粗糙集模型具有更高的整体近似精度。

1 基本概念

在Pawlak经典粗糙集理论中，粗糙集的描述如下：

定义1令（U，R）是一个近似空间，U表示对象的非空有限集合（称为论域），R表示一个二元等价关系，如果，那么称

分别为X在近似空间（U，R）中的下近似和上近似，其中[x]R是x所在的R-等价类。X的近似集合对（X，X）称为X在近似空间（U，R）中的粗糙集[1]。

在Zadeh的模糊集理论中，模糊集的描述如下：

定义2 设A为论域U上的一个模糊集合，它是由 U 上的一个隶属函数 A：U→[0，1]来表示的，A（x）表示元素x隶属于模糊集合A的程度。一般，记F（U）为论域U上模糊集合的全体[9]。

F（U）中两个子集之间的“余集”、“并集”、“交集”和“包含”运算定义如下：

定义 3设 A，B∈F（U），则∀x∈U，规定[9]

（～A）（x）=1-A（x）

（A∪B）（x）=max{A（x），B（x）}

（A∩B）（x）=min{A（x），B（x）}

A⊆B ⇔ A（x）≤ B（x）

2 改进的模糊粗糙集型

2.1 模糊关系

普通关系刻画了两事物间的“精确关系”，也就是说，对于任意两个元素，在其之间或存在关系或不存在关系，两者必居且仅居其一。但在实际生活中，有不少关系很难简单地用“是”或“不是”来衡量。例如，圆与椭圆是否相似，子女与父母长得是否相像，就很难用肯定或否定来做出回答。两者间的相似关系并非非彼即此，而是具有程度上的差异。因此，这种关系就具有模糊性。人们把这种具有程度上差异的关系叫做“模糊关系”。

若X、Y均为有限集，那么可用一个矩阵来表示X到Y的模糊关系的隶属函数值。设X={x1，x2，…，xm}，Y={y1，y2，…，yn}，是 X 到 Y 的一个模糊关系，记为rij=（xi，yj）（i=1，2，…，m；j=1，2，…，n），若所有元素满足 rij∈[0，1]，则称矩阵=[rij]m×n为“模糊矩阵”。

2.2 一般模糊粗糙集

基于模糊关系，孔平等[5]给出了一般模糊粗糙集的定义：

定义4设（U，）为模糊近似空间，为U上的二元模糊关系，则模糊集合B∈F（U）在模糊近似空间（U，）中的下、上近似集仍为模糊集，∀y∈U，其隶属函数分别为

在该模糊粗糙集模型中，其下、上近似集合有以下性质：

若∀A，B∈F（U），则：

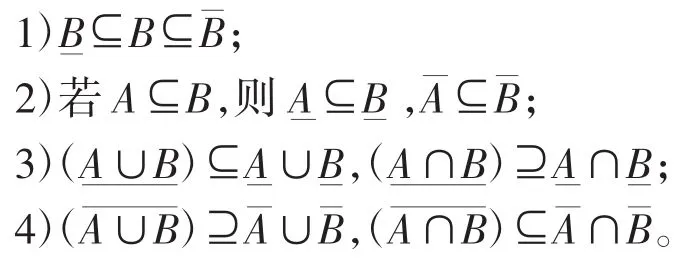
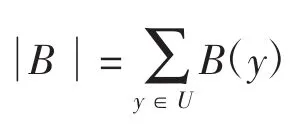
于是，模糊集B的近似精度和粗糙度分别表示为

太极虎冷冷地道：“不懂江湖道义吗？江湖道义该一对一公平搏杀。”萧飞羽耸了一下肩膀道：“夜袭武功堡，擅闯与江湖无争的本庄可曾有过公平？顺带告诉你：我不是江湖人，不会忌惮江湖道义，并且以后我会毫无忌讳用令人齿冷的，或者是龌龊的手段以其人之道还治其人之身！”说完他挥手示意。

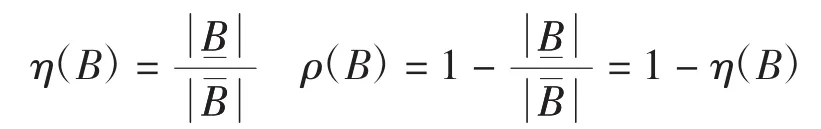
2.3 改进的模糊粗糙集模型

由定义4可看出，一般模糊粗糙集模型仅限于对同一论域上的模糊集合作近似描述，并且近似精度不高。为改善精度及扩大应用范围，本节在一般模糊粗糙集模型的基础上将一个论域扩充成两个论域，并重新给出了模糊集下、上近似算子隶属函数的定义。

定义5若U、V是两个非空的有限论域，是论域U到论域V上的一个模糊关系，则称三元组（U，V，）为双论域模糊近似空间。

下面给出在双论域模糊近似空间中下、上近似算子的定义。

定义6设（U，V，）为双论域模糊近似空间，为U到V上的一个模糊关系，则论域U中的模糊集合B∈F（U）在双论域模糊近似空间（U，V，）中的下、上近似集为论域V中的模糊集，∀y∈V，其隶属函数分别为

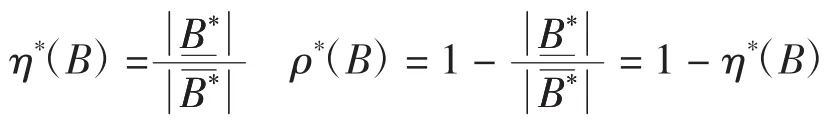
在改进的模糊粗糙集模型中，其下、上近似集合有与一般模糊粗糙集类似的性质。

定理1设∀A，B∈F（U），为U到V上的一个模糊关系，则有：

证明1）由 A⊆B，可知 A（x）≤ B（x），因此

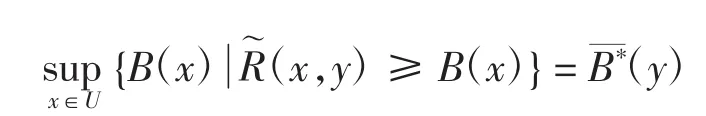
2）由于 A⊆A∪B，可知 A（x）≤（A∪B）（x），又B⊆A∪B，可知 B（x）≤（A∪B）（x），因此

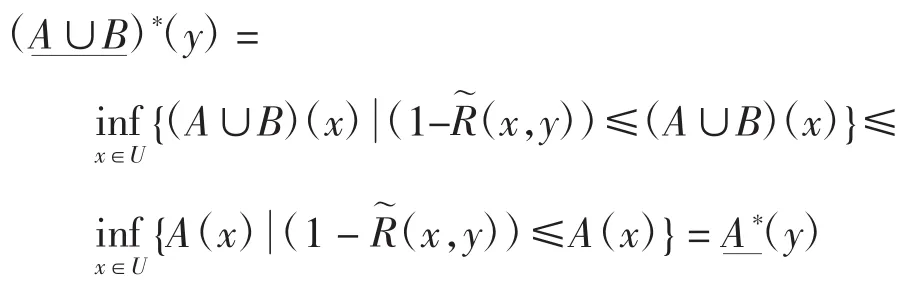
即

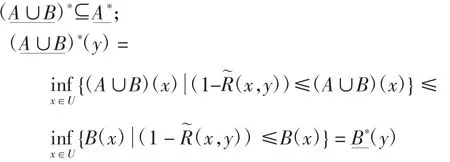
性质3）亦可由上述类似方法证出。

定理2设为模糊集B基于一般模糊粗糙集模型的下、上近似集，为模糊集B基于改进模糊粗糙集模型的下、上近似集，则有

证明事实上，只需证即可。因为

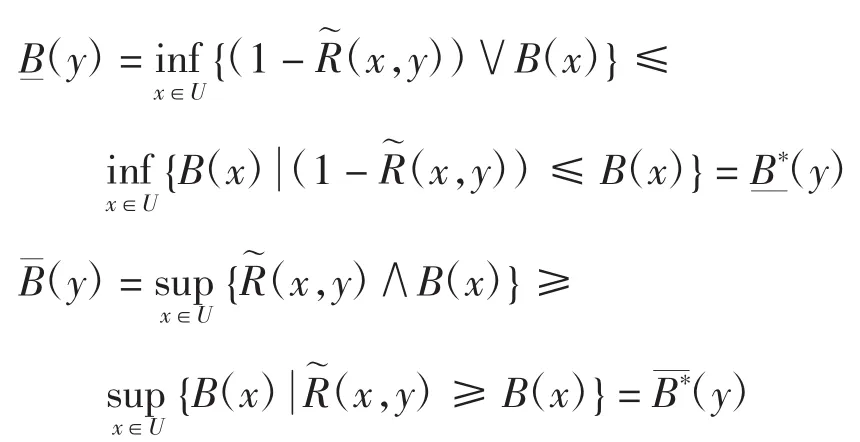
证毕。

定理2说明，改进的模糊粗糙集模型与一般模糊粗糙集模型相比减小了不确定性边界，从而提高了分类精度。

3 实例分析

设某班级中有两个学习小组，用集合U={x1，x2，x3，x4}，V={y1，y2，y3，y4，y5}来表示，则 U 和 V 可看成是两个有限论域。“聪明”是一个模糊概念，通过某种方法对U中4名同学的聪明程度做出了评价，其值分别为0.45、0.78、0.91、0.46，那么通过这种评价构成的模糊集合B记为

B={（x1，0.45），（x2，0.78），（x3，0.91），（x4，0.46）}

在论域与论域之间可以存在着各种各样的模糊关系。如在学生与学生的关系中可有“友好”、“程度相当”等模糊关系。设是论域U到论域V的模糊关系，表示x比y聪明，如表1所示。

表1 模糊关系Tab.1 Fuzzy relation

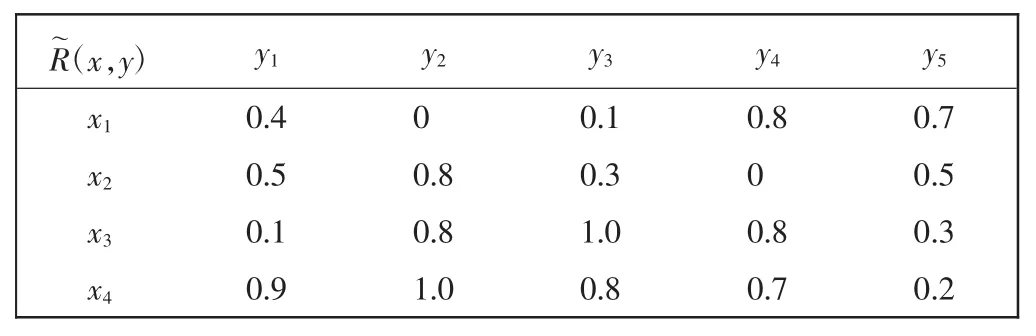
表1 模糊关系Tab.1 Fuzzy relation

R~（x，y） y1 y2 y3 y4 y5 x1 0.4 0.0 0.1 0.8 0.7 x2 0.5 0.8 0.3 0.0 0.5 x3 0.1 0.8 1.0 0.8 0.3 x4 0.9 1.0 0.8 0.7 0.2

根据定义4，计算出模糊集合B的下、上近似集合的隶属函数如下

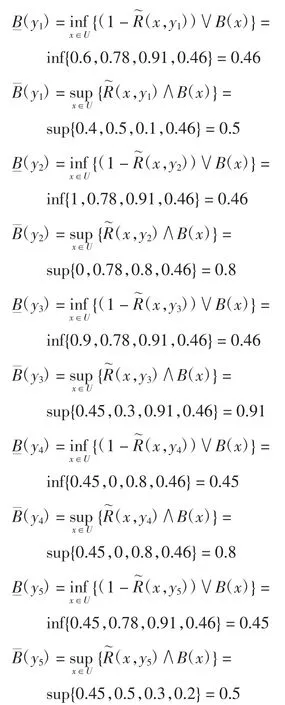
因此，依据一般模糊粗糙集模型，模糊集B的下近似集为

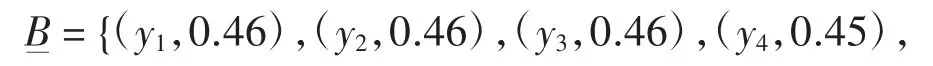
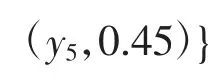
上近似集为

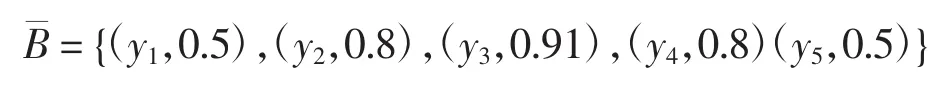
近似精度为

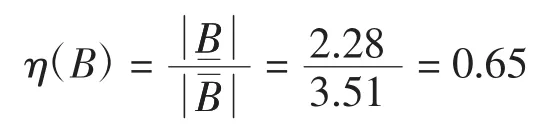
再根据定义6，计算出模糊集合B的下、上近似集合的隶属函数如下

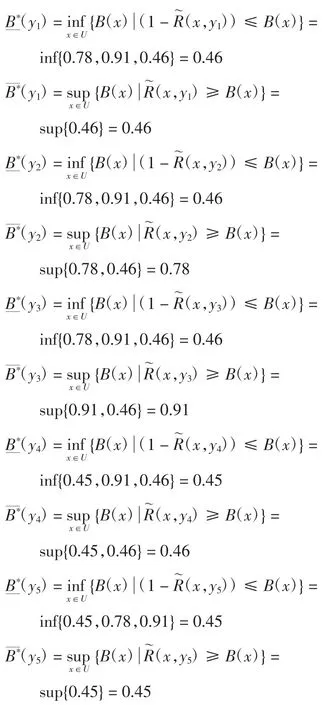
上近似集为

近似精度为

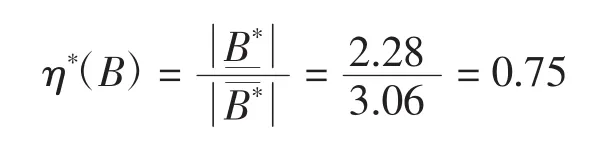
比较上述两部分计算结果，因为η*（B）＞η（B），因此改进的模糊粗糙集模型比一般模糊粗糙集模型有更高的总体近似精度（此例中精度提高10%）。

4 结语

改进的模糊粗糙集模型是在分析了一般模糊粗糙集模型的缺点和不足之后所提出的一种新模型。一般模糊粗糙集模型只能处理一个论域上的问题，无法处理大小不同、元素属性不同的两个不同论域中的问题，而新模型对论域没有过多限制。同时，由于新模型重新定义了模糊粗糙集合的隶属函数，从而使得总体近似精度亦有明显提高。理论分析和实例计算均表明，新模型提供了一种应用范围更广、近似精度更高的模糊粗糙数据分析方法。下一步的工作应是基于本文提出的改进的模糊粗糙集模型，在不完备模糊知识系统中进一步研究属性约简和规则抽取问题，为实际应用奠定理论基础和算法基础。

[1]PAWLAKZ.Roughsets[J].International Journal of Information and Computer Science,1982,11(5):341-356.

[2]张文修,吴志伟,梁吉业,等.粗糙集理论与方法[M].北京:科学出版社,2001.

[3]ZADEH LA.Fuzzy sets[J].Information Control,1965,8:338-353.

[4]DUBOISD,PRADEH.Putting Rough Setsand Fuzzy Sets Together[M]//Intelligent Decision Support.Netherlands:Springer,1992:203-232.

[5]孔 平,张振良.模糊近似空间中模糊粗糙集的新定义[J].曲靖师范学院学报,2005(24):49-51.

[6]司彦飞,刘 超,吴明芬.双论域上的决策粗糙集模型及其刻画[J].五邑大学学报,2014,28(2):20-24.

[7]孙文鑫.基于双论域的一般多粒度模糊粗糙集[J].重庆工商大学学报,2015,32(3):13-15.

[8]LIU Hui,ZHU Feng,LIN Ziqiong.Matrix representation of rough sets based on two universes[J].Computer Engineering and Applications, 2015,51(24):154-158.

[9]梁保松,曹殿立.模糊数学及其应用[M].北京:科学出版社,2007.

Improved fuzzy rough set model

TAO Zhi,PAN Liping,HE Danfeng
（College of Science,CAUC,Tianjin 300300,China）

Fuzzy rough set model is a generalization of classical rough set model.However,it has its own defects and shortcomings.An improved fuzzy rough set model is established on the fuzzy rough set model.One domain is expanded into two domains,and the membership function of fuzzy rough set is redefined.Therefore,the new model’s rough approximation accuracy and application range are effectively improved.This new model is proved to be effective and practical by theory and case analysis.

rough set;fuzzy set;fuzzy relation;fuzzy rough set model

陶志（1963—），男，辽宁沈阳人，教授，博士，研究方向为复杂系统建模、粗糙集理论及其应用等.

TP18

A

1674－5590（2017）05－0060－05

2016-12-07；

2017-02-22

国家自然科学基金项目（60672178）；中国民航大学科研基金项目（2010kys01）

?

杨媛媛）