双论域上基于加权粒度的多粒度粗糙集*

彭连贵 阎瑞霞 陈昭君

（上海工程技术大学管理学院 上海 201620）

1 引言

Pawlak粗糙集理论［1］作为一种处理不精确、不确定与不完全数据的理论，在人工智能、模式识别以及决策分析等方面得到了广泛的应用和研究。

经典粗糙集理论的核心在于利用等价关系从近似空间中导出一对下、上近似算子。因此，粗糙集理论的研究主要集中在三个方面：等价关系、近似空间和论域。针对很多问题中论域上的二元关系不是等价的，学者们研究了基于相似关系、一般关系和优势关系的粗糙集［2］；针对现实生活的模糊性和不确定性，学者们研究了模糊近似空间［3］、变精度［4］和灰色空间下的粗糙集［5］；粗糙集论域扩展的研究是从Yao［6］研究粗糙集代数的信任函数开始的，之后，学者们对论域扩展的粗糙集模型进行了研究。孙文鑫［7］将单论域扩展到了双论域，扩展了其应用性；阎瑞霞等［8］考察了双论域粗糙集的不确定性度量；张超等［9］将模糊语言与粗糙集融合，定义了一种新的粗糙集模型。

Zadeh L.A［10］在1996年提出并讨论的模糊信息粒化问题之后，信息粒化理论［11］在集合理论和区间分析、模糊集、粗糙集、概率论、熵空间理论等架构内不断的发展。Qian 等［12～15］通过分析粒计算与粗糙集理论之间的关联，将粒计算和粗糙集结合起来并提出动态粒度理念，之后将单粒度粗糙集扩展到多粒度粗糙集。多粒度粗糙集模型作为一种新的多视角数据分析方法，克服了经典粗糙集理论的缺陷，在目标识别［16］、Web挖掘［17］、舆情预警决策［18］等众多方面广泛应用。

在多粒度粗糙集研究中，论域与粒度的权重问题一直是学者研究的热点。孙文鑫将单论域扩展到双论域上，却忽略了在实际应用中不是每个粒度都是平等的，有的粒度比较重要，需要赋予更大的权重，而有的粒度作用小，可赋予较小的权重。张明［19］提出了基于加权粒度的多粒度粗糙集，差异地考虑了不同粒度在实际情况下具有不同重要度，却没有放到双论域上进行研究。针对双论域粗糙集在粒度重要程度上考虑的不足和加权多粒度粗糙集在论域扩展上的不足，分析并建立双论域上基于加权的多粒度粗糙集模型，考虑双论域内不同粒度重要程度的差异性，定义粗糙集模型的上下近似并对其性质进行了进一步的研究。

2 双论域粗糙集

定义1［20］设U和V为两个非空有限论域，设R是U和V上的任意二元关系集，且假设，为R的m个属性子集族，′是V和U上R的逆关系。，R和R′的特征函数定义如下：

设论域U中有m个元素，论域V中有n个元素，利用特征函数定义R的关系矩阵记为

显然R′的关系矩阵为矩阵A的转置A'。如果关系矩阵A中不存在一行或一列元素全为零，则称关系矩阵A为信息矩阵。

为了简单描述，将论域U，V和关系R，R′构成的系统记为信息系统（U，V，R），其中U和V为两个非空的有限论域，和互为逆关系。

定义2［20］在信息系统（U，V，R）中，，论域V到论域U的粗糙集近似算子P（U）为

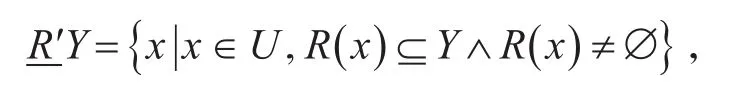
3 双论域上基于加权粒度的多粒度粗糙集

针对多粒度粗糙集论域扩展与属性子集权重研究中的不足，分析并建立双论域上基于加权的多粒度粗糙集模型，在将论域进行扩展的同时，考虑不同粒度所具有的权重的不同。下面给出双论域上的基于加权的多粒度粗糙集模型的定义及其相关性质。

定义3设U，V是两个不同的非空有限论域，设R是U和V上的二元关系集，包含n个属性，且假设为R的m个属性子集划分，（U，V，R）为双论域上的一般近似空间，，由R导出的粒度空间对应的粒度权重为，则对于∀，X关于R的加权多粒度粗糙集的上下近似定义为

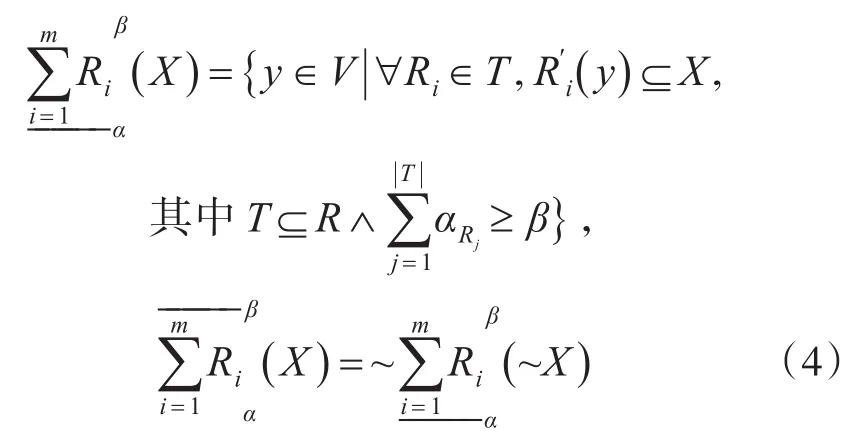
定理1设U，V是两个不同的非空有限论域，设R是U和V上的二元关系集，包含n个属性，且假设为 R 的 m个属性子集划分，（U，V，R）为双论域上的一般近似空间，，由R导出的粒度空间对应的粒度权重为，则有

定理2设U，V是两个不同的非空有限论域，设R是U和V上的二元关系集，包含n个属性，且假设RT=｛R1，R2，…，Rm｝为 R 的 m 个属性子集划分，（U，V，R）为双论域上的一般近似空间，0＜β≤1，由R 导出的粒度空间 U R1，U R2，…，U Rm对应的粒度 权 重 为，对 于，则有

定理3设U，V是两个不同的非空有限论域，设R是U和V上的二元关系集，包含n个属性，且假设为R的m个属性子集划分，（U，V，R）为双论域上的一般近似空间，0＜β≤1，由R导出的粒度空间 U R1，U R2，…，U Rm对应的粒度权重为，有

3）证明过程类似于2）。

定理4设U，V是两个不同的非空有限论域，设R是U和V上的二元关系集，包含n个属性，且假设RT=｛R1，R2，…，Rm｝为 R 的 m个属性子集划分，（U，V，R）为双论域上的一般近似空间，0＜β≤1，由R导出的粒度空间 U R1，U R2，…，U Rm对应的粒度 权 重 为，则 对如果，则有

2）证明过程类似于性质（1）。

定义3设U，V是两个不同的非空有限论域，设R是U和V上的二元关系集，包含n个属性，且假设为的m个属性子集划分，为双论域上的一般近似空间，0＜β≤1，由导出的粒度空间对应的粒度权重为，则对∀Y∈U，X关于R′的加权多粒度粗糙集的上下近似定义为其中，称为Y关于属性子集族R′的双论域上的基于加权粒度的多粒度粗糙集。

4 算例应用

双论域上基于加权粒度的多粒度粗糙集在将论域扩展的同时考虑粒度的不同重要性的现实情况，在现实中的应聘案例中有很好的应用性。表1～3描述的是外贸公司选聘人才的情况，其中是由该外贸公司五位应聘者组成的一个论域，是由公司要求应聘者要具备的技能构成的一个论域。其中y1表示的是口才表达，y2表示的是专业技能，y3表示的是英语技能，y4表示的是工作态度。应聘者分别由一位主面试官，两位副面试官为其打分，其中数字1表示该应聘者具备此项能力，0表示该应聘者不具备此项能力。

表1 专家1打分情况表

表2 专家2打分情况表

表3 专家3打分情况表

根据AHP方法，确定专家1、专家2、专家3对应的权重分配为。通过专家对应聘者的评估，我们知道这五位应聘者成功应聘的为。试问在满足题设条件的情况下，这五位应聘者要想都应聘成功，必须具备哪几项能力，应该具备哪些能力。根据定义3计算得

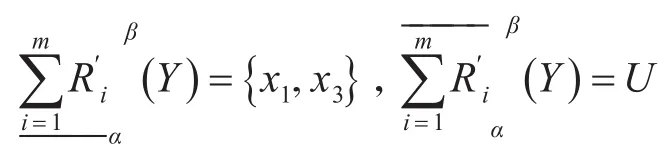
比较文献［7］中粗糙集模型的运算结果发现：阈值β=2/3的题设情况下，双论域粗糙集在进行运算时遍历；而文中提出的粗糙集模型可以有选择的访问或来进行运算。且在计算机中设计运算时，首先选择或，而不会选择访问，时间效率提高了33%；当在情况下，遍历所有的属性子集，必然造成冗余运算和时间的浪费；而双论域上基于加权的多粒度粗糙集却很好地克服了这一点，从可以知道，该模型在满足一定权值积累的要求时即可；关注那些对事件发展具有显著影响的因子，可以大大提高事件处理的效率。将该模型运算的结果。与文献［19］模型的运算结果进行对比发现，该模型具有更高的精确度。

5 结语

粗糙集处理模糊信息的优越性，使其广泛应用于诸多领域。为了克服双论域上基于一般关系的多粒度粗糙集在属性子集权重上考虑的不足与加权多粒度粗糙集在论域扩展问题上讨论的不足，分析并建立双论域上的基于加权的多粒度粗糙集模型。通过实例的分析验证发现：该模型不仅在处理简单问题具有很好的效果，而且在处理复杂事件时，也能够很好地解决问题，同时在保证运算精度的情况下，节约运算的时间，提高效率。

文章提出一种新的粗糙集模型仍需要继续深入研究该模型的不确定性度量和稳定性，以及在实际生活中的应用等问题，不断将其优化，使其发挥更大的作用。