动态更新属性值变化时的最优粒度
刘凤玲,林国平
(闽南师范大学 数学与统计学院,福建 漳州 363000)
1 引 言
数据规模随着信息技术的迅速发展而不断膨胀,粒计算常用于处理复杂的数据系统.粒计算是将所需探究的论域划分成若干相对简单的粒,簇、块或集合构成了这些粒.
Zadeh于1979年首次提出模糊信息粒这一概念[1].随后,相关应用背景的粒计算模型与方法相继被提出[2-5].信息粒在解决复杂问题中起重要作用,其可将较为复杂的信息系统抽象地转化为若干相对简单的信息系统,这样既可以降低处理难度,又可以提高预测信息的准确性.
在大部分信息系统中,同一对象在同一个属性下只有一个属性值,这使得人们只能从固定的粒度或视角分析数据信息.然而,在实际应用中,根据实际问题的不同需要,同一个对象在同一个属性下可以取不同粒度层次标记的值. 例如,需要评定奖学金时学生的考试成绩一般记录为0~100之间的数,需要知晓成绩优秀、较好等级别的人数时可以将成绩记为“优秀”、“较好”、“中等”、“差”. 进一步的,如果需要,还可以将其分为两个值,比如给予学位认定时记为“合格”和“不合格”.基于此,Wu等人根据对象在决策系统中拥有不同的粒度标记,于2011年首次给出了多粒度标记决策系统的概念[6].近年来,基于多粒度标记划分的粗糙集数据分析方法得到不断完善和发展,多粒度标记决策系统是人们研究的热点. 目前,查阅相关文献发现学者们主要从最优粒度选择[7-17]、规则约简或提取[18,19]及知识表示[20]等方面对多粒度标记决策系统进行研究. 从系统的协调性与完备性的角度来看,学者们主要研究了协调且完备的、协调不完备的以及不协调但完备的这三种多粒度标记决策系统.在实际应用中,多粒度标记决策系统是常被用于各种信息分析,如被广泛应用于数据挖掘、图像处理、人工智能、地理信息甄别和军事技术等领域.
如今是大数据时代,在许多实际情况下,由于各种需求或人为失误,数据可能会发生变化.因此,需要对动态数据集中隐藏的知识进行相应的更新. 增量更新机制是利用前面获得的计算结果来获取动态数据集中的知识而不是重新从头开始计算.在动态环境中,目前基于粗糙集理论的增量更新方法主要涉及对象的变化[21-23]、属性的变化[24,25]以及属性值的变化[26,27].而有关多粒度标记决策系统方面的动态更新,本人只查阅到学者们讨论了在多粒度决策系统中,对象更新环境下选择最优粒度的策略并设计了相应的算法.
事实上,在实际应用中人为或其他因素难免不出现收集到的多粒度标记决策系统在某个粒度标记下的属性值是错误的,而此时则需要将正确的属性值更新进去,从而得正确的数据,即此时新的系统属性值发生了更新.若当前粒度尺度下属性值发生变化,则粗于该粒度尺度的粒度尺度可能也随之发生变化.一般来说,在多粒度标记系统中等级越小的粒度越细,然而粒越细获取知识的成本越高,因此选择合适的粒度级别来获取规则及求目标近似集等较为重要,即最优粒度选择是多粒度标记系统中的知识获取较为关键的一步.基于此,本文针对属性值变化环境下的不协调多粒度决策系统最优粒度的选择进行研究.
由于WU在文献[9]中分析了不协调多粒度决策系统中8种不协调性选择最优粒度的对比,指出实际上只有4种:分布协调; 最大分布协调;而分配协调、似然协调、上近似协调及广义协调互相等价; 下近似协调与信任协调等价.基于此,本文将只讨论4种协调性下属性值变化环境下的不协调多粒度决策系统选择最优粒度的策略:分布协调、最大分布协调、上近似协调及下近似协调.
2 基本知识
2.1 多粒度标记决策系统的概念
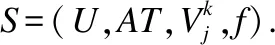
在多粒度标记系统中,每一个属性aj∈AT均为多粒度标记属性,也即对于同一个对象x∈U在不同粒度层面下有不同的取值.为方便讨论,本文约定没有特别说明情况下在同一系统中,所有条件属性的粒度层次均为I.
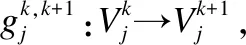

对任意的Ck⊆C,将论域U在Ck下的等价关系、等价类及等价划分分别记为:
类似记:R{d}={(x,y)∈U×U|f{d}(x)=f{d}(x)},[x]{d}={y∈U|(x,y)∈R{d}},U/R{d}={[x]{d}|x∈U}={D1,D2,…,Dr},r为决策类划分的个数,即r=|U/R{d}|.
对于论域U中的一个子集X,其关于RCk的下近似和上近似分别为:
若对任意的[x]RCk∈U/RCk,总存在[x]Rd∈U/R{d}使得[x]RCk⊆[x]Rd成立,则记RCk⊆Rd.
假设dIS=(U,C∪{d})为一个多决策的多粒度标记决策系统,该系统中所有条件属性均有I个等级粒度,则dIS=(U,C∪{d})可分解为I个信息系统,也即dIS=dIS1∪dIS2∪…∪dISI.
2.2 不协调多粒度标记决策系统的协调性与最优粒度选择
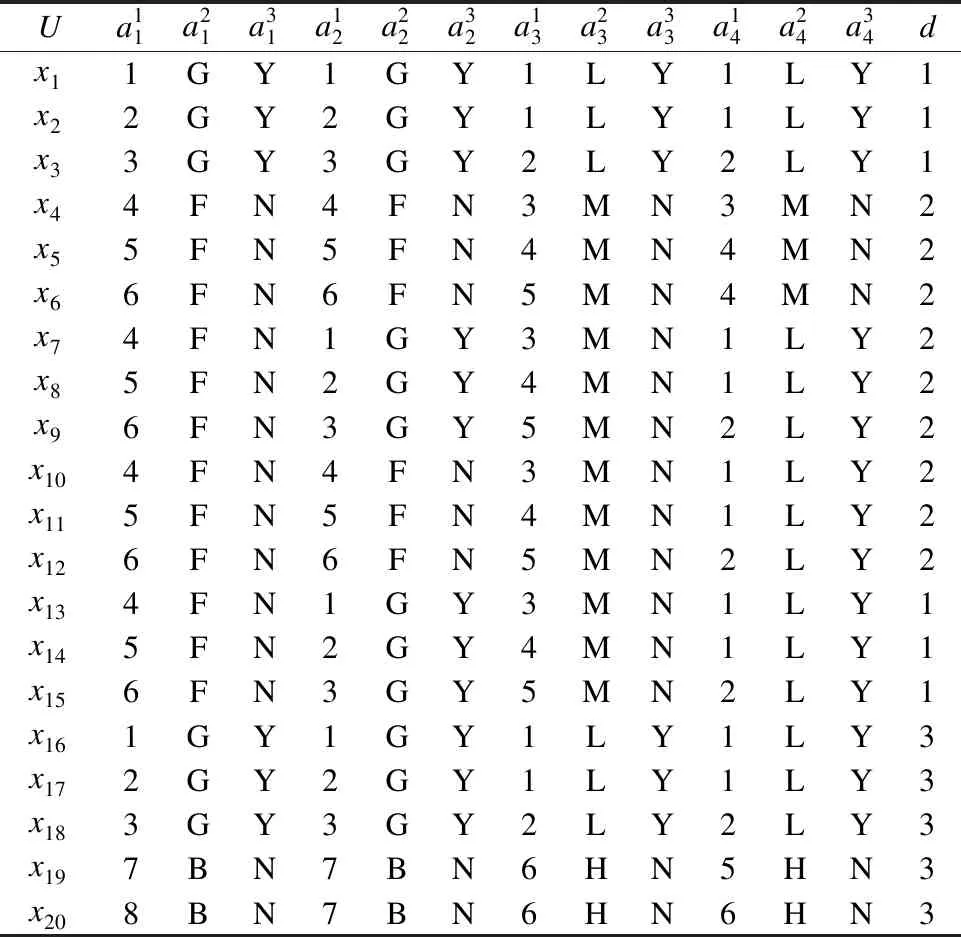
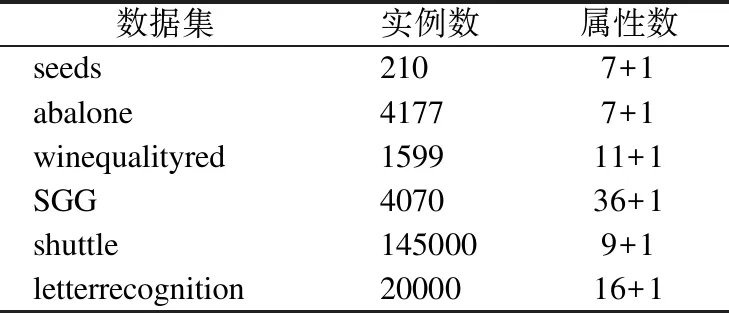
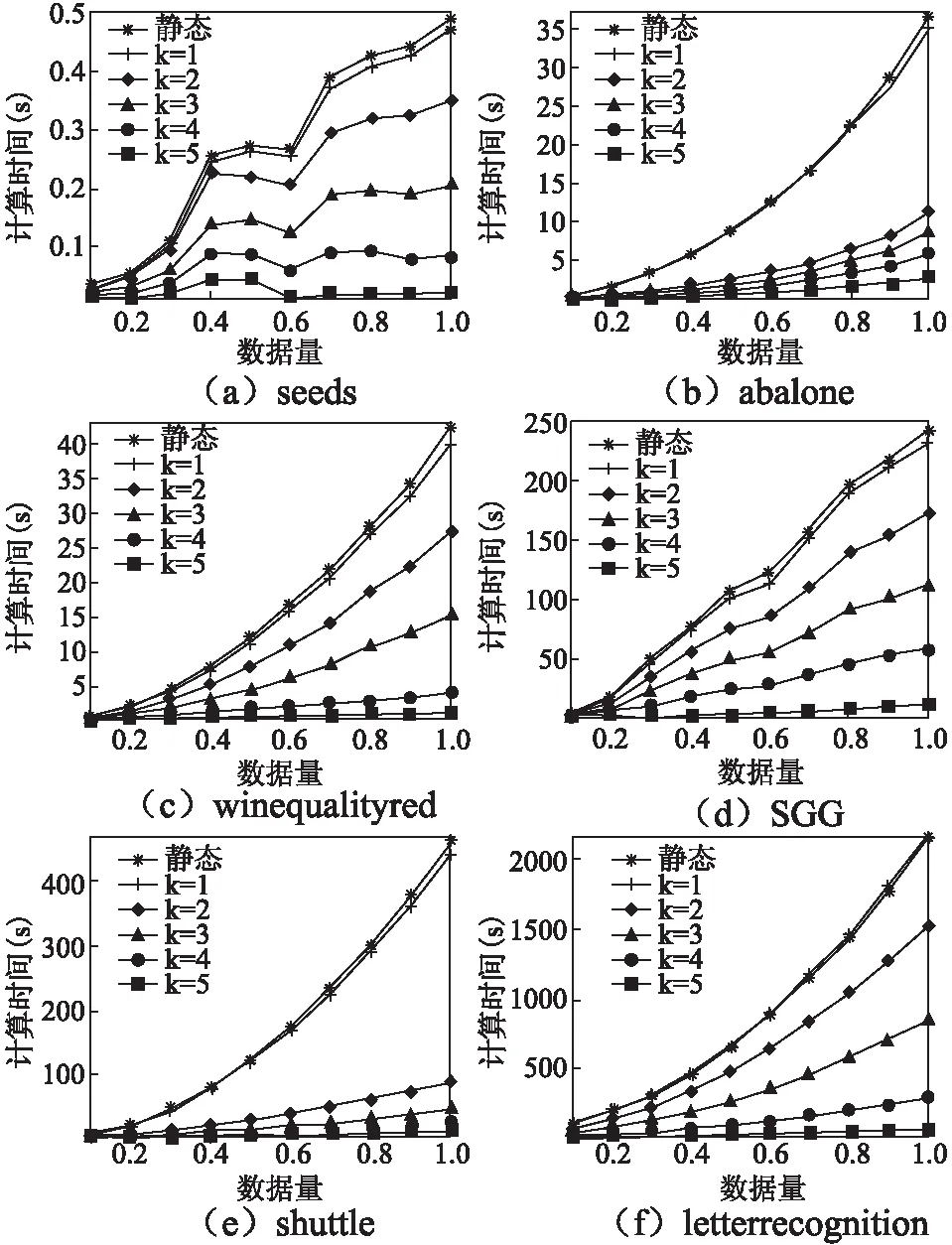
定义3[6].设dIS=(U,C∪{d})为多粒度决策系统,若RC1⊆Rd,则系统dIS是协调的.若进一步满足RCk⊆Rd,则称dISk=(U,Ck∪{d})协调.若dISk=(U,Ck∪{d})协调,则对任意的k′ 定义4[9].设dIS=(U,C∪{d})为不协调的多粒度决策系统,则 1)如果LCk(d)=LC1(d),就称dISk关于dIS下近似协调.若dISk关于dIS下近似协调,但若k+1≤I,dISk+1关于dIS不是下近似协调,那么S的下近似最优粒度为第k粒度层次. 2)如果HCk(d)=HC1(d),就称dISk关于dIS上近似协调.若dISk关于dIS上近似协调,但如果k+1≤I,dISk+1关于dIS不是上近似协调,那么S的下近似最优粒度为第k粒度层次. 3)如果对任意的x∈U,有μCk(d)=μC1(d),就称dISk关于dIS分布协调.若dISk关于dIS分布协调,但若k+1≤I,dISk+1关于dIS不是分布协调,那么S的分布最优粒度为第k粒度层次. 4)如果对任意的x∈U,有γCk(d)=γC1(d),就称dISk关于dIS最大分布协调.若dISk关于dIS最大分布协调,但若k+1≤I,dISk+1关于dIS不是最大分布协调,那么S的最大分布最优粒度为第k粒度层次. 定理1.设在t时刻,不协调多粒度决策系统为dIS(t)=(U,C∪{d}),且系统dIS(t)的下近似最优粒度层次为第kt粒度层次;在t+1时刻,k′ 1)当k>kt+1时,则kt+1=kt; 2)当k≤kt+1时,若dISk关于dISt+1不是下近似协调的,则kt+1=k-1;若dISk关于dISt+1是下近似协调的,则判断k+1的下近似协调性,若dISk+1关于dISt+1是下近似协调的,则继续判断k+2的下近似协调性,以此循环,直至k+m关于dISt+1不是下近似协调的,则kt+1=k+m-1. 证明:在t时刻,系统dIS(t)的下近似最优粒度层次为第kt粒度层次,则由定义4易知,对任意的k′≤kt,dISk′均关于dISt是下近似协调的;dISkt+1关于dISt不下近似协调. 1)若k>kt+1,则说明在t+1时刻,任意的k′≤kt+1所对应的属性值均未发生变化.此时对任意的k′≤kt+1,dISk′均关于dISt+1是下近似协调的,又dISkt+1关于dISt+1不是下近似协调的,从而由定义4可知t+1时刻系统的下近似最优粒度为kt.即可得kt+1=kt. 2)若k≤kt+1,则说明任意的k′≤k-1所对应的属性值均未发生变化.即此时对任意的k′≤k-1,dISk′均关于dISt+1是下近似协调的.若dISk关于dISt+1不是下近似协调的,又dISk-1关于dISt+1是下近似协调的,则由定义4可知t+1时刻系统的下近似最优粒度层次为k-1;若dISk关于dISt+1下近似协调则由定义4中的(1)可知成立. 下面给出例子来分析及理解所提出的定理. 例1.如表1为一个多粒度标记决策系统,记为dIS=(U,C∪{d}).该表的条件属性有三个粒度层次,其中“G,F,B,S,M,L,Y,N”分别表示“好,中等,差,小,中,大,是,否”.按粒度层次该信息表可分解为三个信息表,即dIS=dIS1∪dIS2∪dIS3,其中, 表1 多决策的多粒度标记信息表Table 1 Multi-granular labeled table with multi-decision 定理2.设在t时刻,不协调多粒度决策系统为dIS(t)=(U,C∪{d}),且系统dIS(t)的上近似最优粒度层次为第kt粒度层次;在t+1时刻,k′ 1)当k>kt+1时,则kt+1=kt; 2)当k≤kt+1时, 若dISk关于dISt+1不是上近似协调的,则kt+1=k-1; 若dISk关于dISt+1是上近似协调的,则判断k+1的上近似协调性,若dISk+1关于dISt+1是上近似协调的,则继续判断k+2的上近似协调性,以此循环,直至k+m关于dISt+1不是上近似协调的,则kt+1=k+m-1. 定理3.设在t时刻,不协调多粒度决策系统为dIS(t)=(U,C∪{d}),且系统dIS(t)的分布最优粒度层次为第kt粒度层次;在t+1时刻,k′ 1)当k>kt+1时,则kt+1=kt; 2)当k≤kt+1时, 若dISk关于dISt+1不是分布协调的,则kt+1=k-1; 若dISk关于dISt+1是分布协调的,则判断k+1的分布协调性,若dISk+1关于dISt+1是分布协调的,则继续判断k+2的分布协调性,以此循环,直至k+m关于dISt+1不是分布协调的,则kt+1=k+m-1. 定理4.设在t时刻,不协调多粒度决策系统为dIS(t)=(U,C∪{d}),且系统dIS(t)的最大分布最优粒度层次为第kt粒度层次;在t+1时刻,k' 1)当k>kt+1时,则kt+1=kt; 2)当k≤kt+1时, 若dISk关于dISt+1不是最大分布协调的,则kt+1=k-1; 若dISk关于dISt+1是最大分布协调的,则判断k+1的最大分布协调性,若dISk+1关于dISt+1是最大分布协调的,则继续判断k+2的最大分布似协调性,以此循环,直至k+m关于dISt+1不是最大分布协调的,则kt+1=k+m-1. 下面以下近似协调为例给出相应的静态算法和动态算法. 算法1.静态:多粒度决策系统的最优粒度选择 输入:t+1时刻求得的多粒度决策系统dIS(t+1)=(U,C∪{d}). 输出:多粒度决策表的最优粒度kt+1. Step1.计算决策划分U/Rd={D1,D2,…,Dr},k′=1; Step2.当k′=1:|I|时,则计算[x]Ck′(x∈U); Step3.当k′=1:|I|时,求出LCk′(d); Step4.判断LCk′(d)与LC1(d) 的关系,若LCk′(d)≠LC1(d),则kt+1=kt-1,停止运算.若LCk′(d)=LC1(d),则转Step 5. Step5.若k′+1>I,则kk+1=k′,停止运算;若k′+1≤I,则k′=k′+1,并转到Step 2. 算法2.动态:多粒度决策系统在属性值更新环境下的最优粒度选择 输入:t时刻求得的多粒度决策系统dIS(t)=(U,C∪{d})及其最优粒度层次kt及其决策划分{D1,D2, …,Dr}、t+1时刻的多粒度决策系统dIS(t+1),属性值变化的最小粒度层次k. 输出:多粒度决策表在属性值更新之后的最优粒度kt+1. Step1.判断k与kt+1的大小关系,若k>kt+1,则转Step2;若k≤kt+1,则转Step3; Step2.kt+1=kt,停止运算; Step3.当k′=k:|I|时,求出LCk′(d);判断LCk′(d)与LC1(d) 的关系,若LCk′(d)≠LC1(d),则kt+1=kt-1,停止运算,若LCk′(d)=LC1(d),则转Step 4. Step4.若k′+1>I,则kt+1=kt,停止运算;若k′+1≤I,则k′=k′+1,并转回Step 3. 这部分通过在6个UCI数据集来比较静态和动态算法的计算性能.6个数据集的相关信息见表2. 表2 数据集描述Table 2 Data set description 在这个实验中,比较了随着数据规模增大,静态和动态算法的执行时间.所有的算法运行在个人电脑,配置Windows 7,Intel(R)Core(TM)i7-3632QM CPU 2.20GHz,4GB内存.编程语言matalb. 将预处理好的每个数据集分割为等大小的10份.第1份作为第1个数据集,第1和第2份的组合作为第2个数据集,第2个数据集和第3份数据的组合作为第3个数据集,以此类推,全部10份的数据组合作为第10个数据集.10个数据集的目标概念都使用所对应的数据集的决策类.这10个数据集可以用来观察静态和动态算法执行时间随着数据集规模增大的变化情况. 在本小节中,不失一般性,对于所有粒度标记下属性值变化的可能都进行了实验,即对k=1,2,3,4,5这五种情况都进行了静态和动态的实验.由于k=1,2,3,4,5时静态算法的计算时间一致,故本文只罗列一次.为了公平,两个算法没有进行其它的优化. 图1 静态和动态算法最优粒度选择的计算时间比较Fig.1 Comparison of computation time of optimal scale selection between static and dynamic algorithms 实验结果见图1和表3.图1展示了两个算法计算时间随数据集规模的变化情况.从图1(x轴表示数据集占总数据的比例,y轴表示计算时间)不难发现,对于相同的大小的数据集,当k≥2时静态最优粒度选择算法时间消耗一致地低于静态最优粒度选择算法.另外,在大多数数据中,计算时间的差值随着数据的增加而增大.k=1时计算时间基本持平.表3展示了两个算法在6个数据集各自产生的第10个数据集上的运行时间.结果显示局部多粒度下近似算法仅仅花费了相应全局算法的十分之一执行时间. 表3 静态和动态算法计算时间比较(时间:秒)Table 3 Comparison of computation time between static and dynamic algorithms(time:s) 研究了某个粒度下属性值变化时最优粒度的选择策略,并设计了相应的静态和动态最优粒度选择算法并进行了相关实验.实验结果表明,新提出的方法可以对于属性值变化的系统可以有效进行选择最优粒度,且设计的动态最优粒度选择算法在一定程度上提高了计算效率.
3 属性值变化环境下的不协调多粒度决策系统的最优粒度选择
4 属性值变化环境下的不协调多粒度决策系统的最优粒度选择算法
5 实验分析
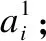

6 结 语

