双分数随机利率环境下汇率连动期权定价*

刘淑琴 薛 红

（西安工程大学理学院 西安 710048）

1 引言

当前期权渐渐吸引了国内国外许多投资人的眼球，其定价也越来越引起人们的重视。因此学者们也对不同期权进行了研究，文献［1～3］分别讨论了重置期权，回望期权，亚式期权的定价问题。现汇率连动期权作为期权的一种，是进行全球投资的一种金融期权形式，不仅依赖于外国股票的价格，而且依赖汇率变化。因为国标的资产和汇率的变动都是随机过程，定价比较困难，所以许多学者对此期权也进行了研究。迄今为止，有关汇率连动期权的研究也有许多，文献［4～12］主要利用鞅方法和保险精算方法等不同方法分别讨论了布朗运动环境下有关汇率连动期权定价模型，并给出了相应的定价公式；以上学者是在布朗运动环境下研究的此期权，然而我们发现，分数布朗运动具有较好的“厚尾”和长程依赖特性，因此用分数布朗运动取代了标准布朗运动。文献［13～14］利用不同的方法讨论了标的资产服从分数布朗运动下汇率期权定价问题；但是近年来，发现双分数布朗运动没有独立性和平稳性，使用范围比较广，即可描述平稳又可描述不平稳的现象，比分数运动是更一般的高斯过程。文献［15］国外学者首次提出了双分数布朗运动，它是更一般的Gauss过程，它的增量与增量之间无独立性，无平稳性的特征，相对分数布朗运动适用范围更加广泛，所以可以更好地应用到金融市场当中。随后文献［16～20］基于双分数布朗运动驱动环境下讨论了各种期权定价模型，结果都优于分数布朗运动环境下的模型。期权定价的方法有多种多样，但适用范围较广，限制因素较少的是由文献［21］是由 Mogens Bladt与 Tina Hvid Rydberg于1998年第一次提出的保险精算方法。在文献［22］中闫海峰等人也讨论了此方法的优点。文献［23］中讨论了欧式期权和交换期权在随机利率及O-U过程下的定价方法。基于诸多学者研究的基础上，因此本文在股价和汇率满足双分数随机利率驱动的随机微分方程的大前提下，利用此方法推导出汇率连动期权定价公式。

2 金融市场数学模型

假定利率rt，股票价格St，汇率价格 Xt分别满足随机微分方程：

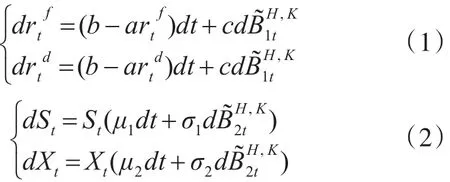
其中 a，b，c，μt，σ 为常数，，都为双分数布朗运动，并且它们的相关系数都为δ。

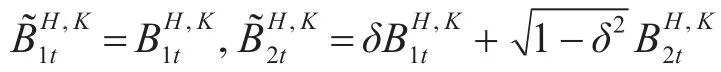
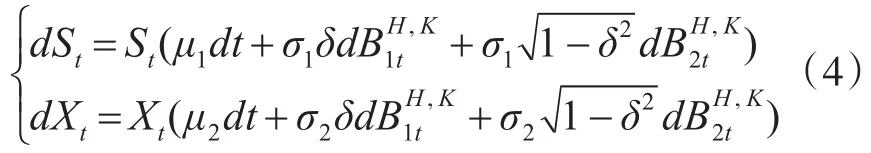
引理1 随机微分方程（3）的解为

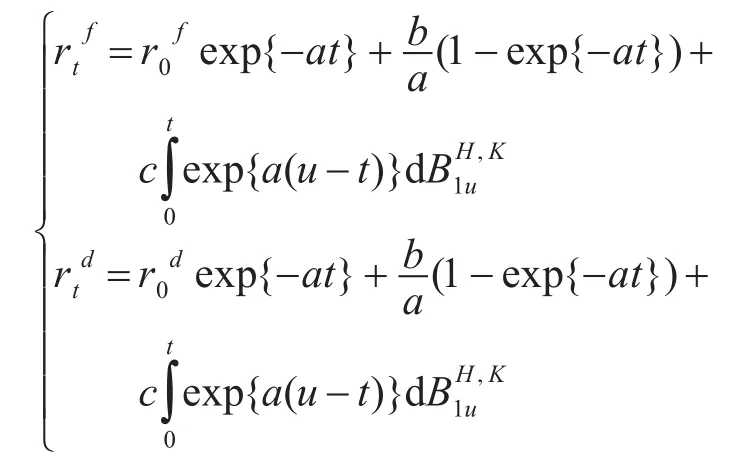
引理2 随机微分方程（4）的解为

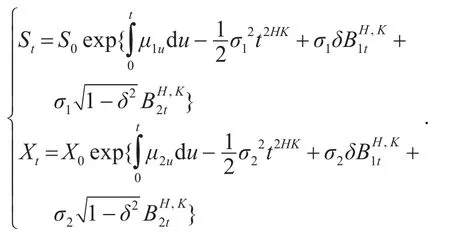
定义1［20］价格过程在 [t，T]的期望收益率定义为。

引 理 3［23］设 两 随 机 变 量 ，，则对任意实数 a，b，c，d，k，有

引 理 4［23］设 三 随 机 变 量 ，，则 对 任 意 实 数a，b，c，k，有

3 汇率连动期权定价

3.1 第一种汇率连动期权

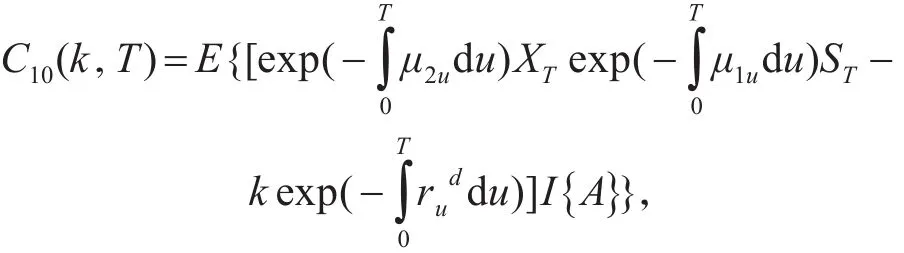
其中：

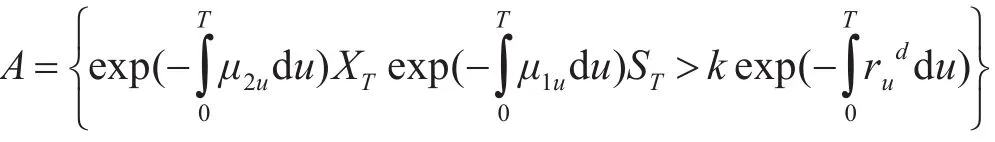
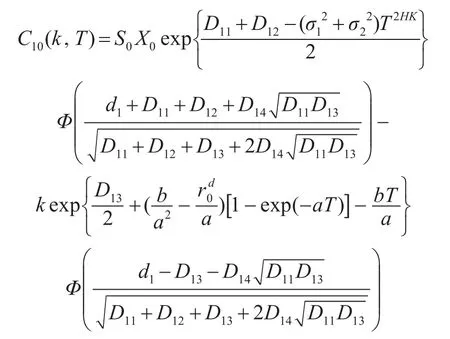
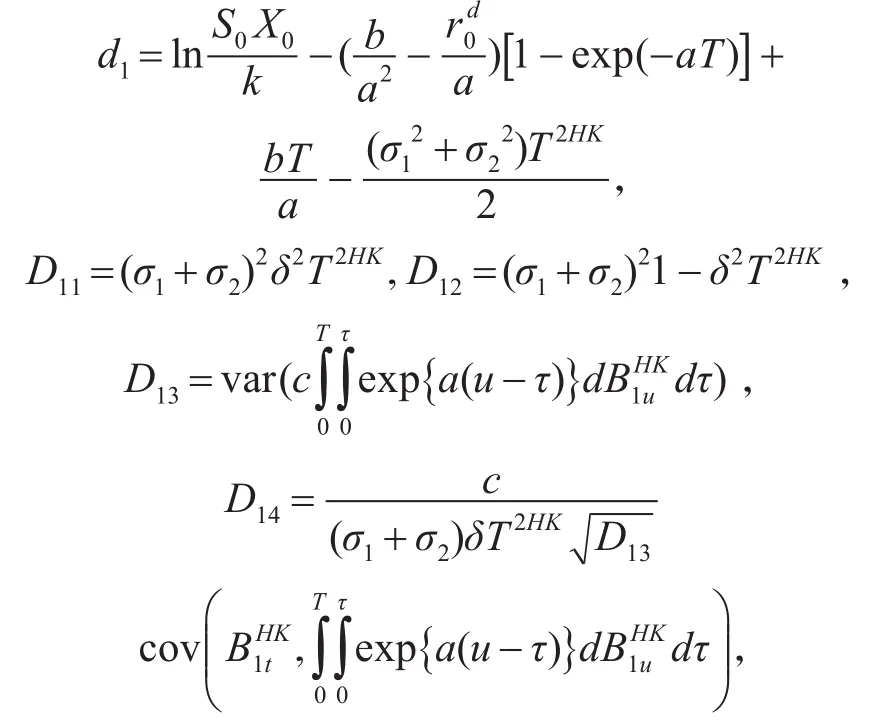
证明：首先

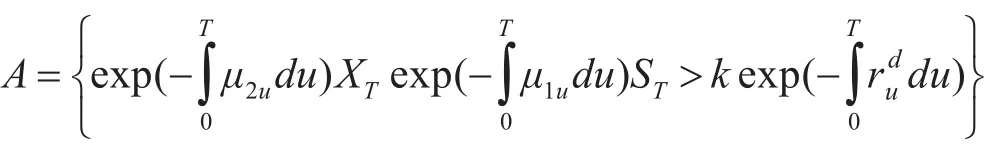
由于

其中：

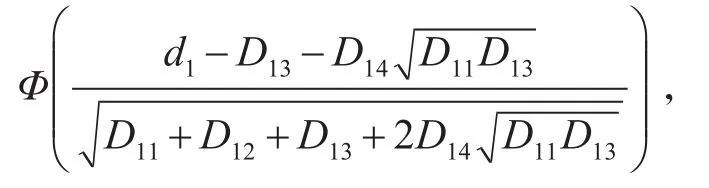
由于

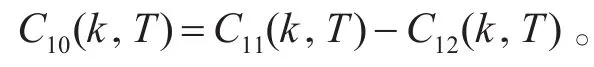
故结论得证。

3.2 第二种汇率连动期权

其中：

证明：首先

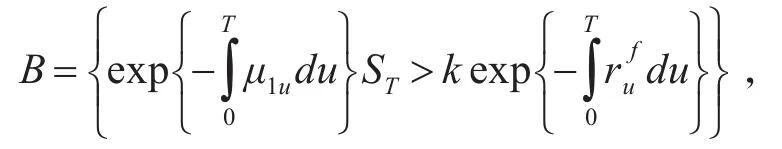
则

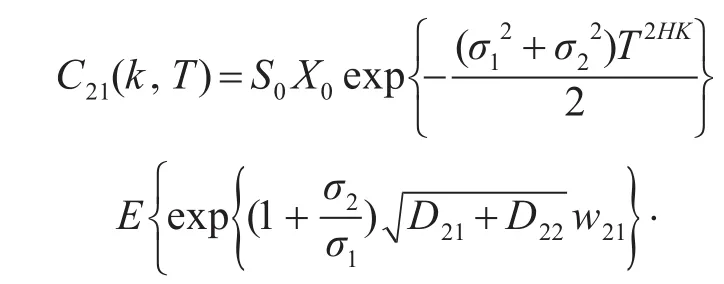
由于

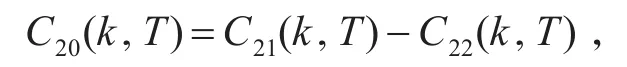
故结论得证。

4 结语

当前有越来越多的证券投资商以及各种商业银行发行了汇率连动期权，但由于股价以及汇率的变动都是随机的变动过程，对其定价相对来说有一定的难度，因此本文利用保险精算进行贴现定价方法在双分数随机利率下定价了此种期权，不论金融市场处于以上何种情况，本文给出的汇率连动期权公式都能使用。