基于神经网络算法的配电网重构研究*
庄 剑
(国网天津市电力公司 天津 300010)
1 引言
电力公司一直在寻找新技术,以提高电力输送性能[1]。其中,功率损耗的控制是一个重要问题。配电网的功率损耗计算可以采用以下几种策略:1)电容器组[2];2)相平衡[3];3)配电馈线重构[4]。其中,配电馈线重构是指在发生突发事件时,通过系统损耗最小化或服务恢复时间最小化,以控制开关来改变系统拓扑结构。因此,这需要构造不同的目标优化问题。在系统损耗的情况下,主要关心的是尽量减少有功功率损耗。无功功率损耗[5]、停电次数[6]和恢复时间[7]等因素是电力系统恢复过程中需要最小化的决策变量,对于这两类问题,数学模型是一个非线性混合整数问题[8]。本文讨论配电系统有功损耗最小化问题。现有的重构问题的损失最小化解决方法可以被分成两类:启发式算法[9]和人工智能算法[10]。其中,启发式算法一般只确定一个特定负载条件的解决方案,通常利用交互过程达到该负载条件。人工智能算法可通过人工神经网络(ANN)[11]在实时模式下为每个负载模式提供一组高质量的拓扑,而不执行迭代过程。也就是说,在不执行大规模迭代过程的情况下,当负载配置文件发生变化时,人工神经网络可以提供解决方案。
本文提出了一个考虑到上述问题的人工神经网络。人工神经网络只使用一个神经网络,并以确定最合适的拓扑结构进行计算。为了提高人工神经网络的性能和结构,本文结合了聚类技术以减少人工神经网络输入数据的数量。通过使用聚类技术的训练集确定算法达到最好的性能,从而产生一个更有效的信息源的人工神经网络。其结果使得人工神经网络具有更强的泛化能力,并有可能确定高品质的拓扑与较低的损失。
2 数学建模
配电系统重构的目标是确定最小有功功率损耗的拓扑结构。所提出的数学模型如下:
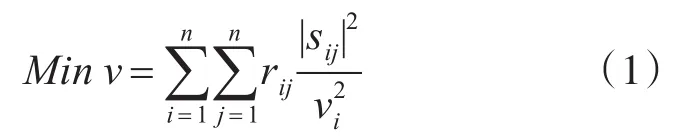
使得
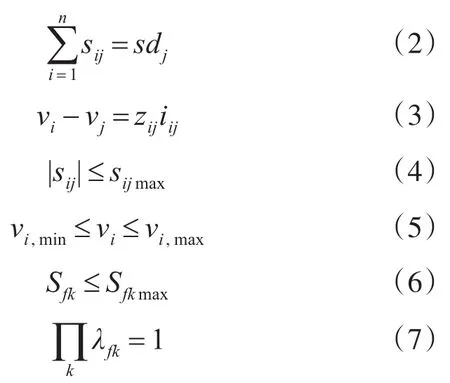
其中,n为配电网系统中的节点数量,sij、iij和zij分别为支路的功率流、电流和阻抗。sdj为总线上节点 j的负载,vi为节点i上的电压,Sfk为馈线 fk上的功率流,如果终端总线和电源之间只有一条路径,则等于1,否则为零。
在建立的数学建模公式中,目标函数式(1)表示系统中的有功损耗;约束条件(2)和(3)代表基尔霍夫定律;约束条件(4)和(5)表示支路的电压流和应保持在限值内的电压;约束条件(6)是变电站变压器的运行限值;约束条件(7)是使系统的径向度约束。相应的数学模型是一个混合整数非线性规划问题(MINLP)。
3 神经网络算法
3.1 神经网络
人工神经网络简称为神经网络(NN),它是一种有组织的密集连接节点系统[12],通常采用前馈方式。每个连接(或神经元)都与一个称为权重的数字相关联[13]。本文所描述的神经网络是一种标准的多层感知器。如图1所示,又称为m-n-k网,它代表m个神经元接收来自外部世界的信息输入层的神经网络,隐藏层神经元的n(传播信息)和输出层的神经元k提供了整个网络的响应。
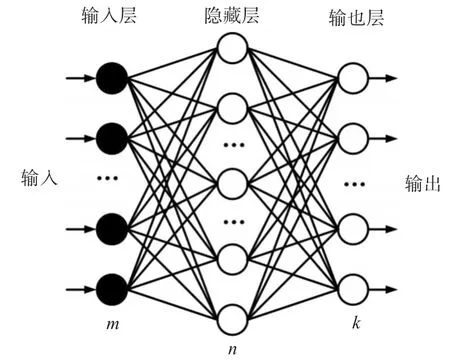
图1 多层神经网络感知器
一个神经网络的输出O可以定义为输入I的函数和形式为O=φ(I,W)的权重W ,其中 φ表示由NN定义的映射函数φ:Rm→Rk。神经网络训练过程包括调整权值wij,以实现训练数据的“良好”映射。因此,对于悬链具有未知数学关系的数据[14],神经网络提供了映射。执行映射的数据集以下面的形式表示:
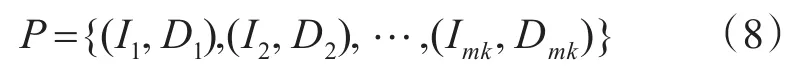
其中,(Ii,Di)表示训练模式i的输入和输出期望。训练算法寻找具有调整和泛化训练集的映射函数φ,泛化是神经网络为不属于训练集的输入提供足够的输出的能力。根据输入Ii及其相应的输出期望Oi,训练过程使得能量函数E最小化,这是所有元素P训练集中D和O之间的平均二次误差:
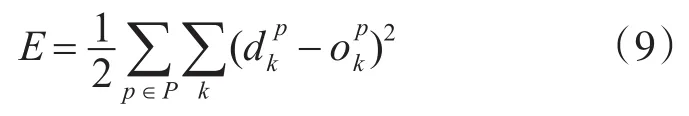
对于E(W)≥0,该算法对于所有的训练集,即理想条件使得代价函数等于零的权重的组合,试图找到一个集合W'使得E(W')=0。然而,由于映射函数φ在不同层的传递是非线性的,且训练算法是一个迭代过程,使得给定的平均二次误差式(9)最小化,这可用于优化无约束非线性问题的任何算法。
利用经典的一阶和二阶算法确定方向。对于第一种情况,通过使用目标函数(9)的梯度来实现,它们被称为反向传播算法或梯度后代。这些算法速度快,唯一的缺点是反向传播只能应用于具有可微函数的网络。训练算法根据搜索方向r(t)改变权值:
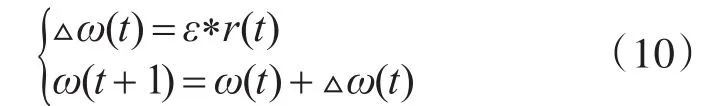
另一类是由共轭梯度法[15]和拟牛顿法[16]、Levenberg-Marquardt法[17]等算法构成的,即为了简化高阶导数,表现出良好的性能。
3.2 聚类技术
聚类技术作为分析和创建具有相似特征的数学工具,具有识别和恢复每个标识组的未知特征。本文提出了一种基于需求值的聚类方法。它没有考虑到配电网系统的地理局限性。因此,只考虑有功和无功功率。这种方法产生了一组完全代表系统所有需求的负载。应用聚类技术的一个结果确定输入层神经元,从而提高了神经网络的性能。
聚类技术考虑了两个基本标准[18]:邻近度量和分组标准。邻近度量表示两个点之间的相似程度,并考虑到系统的特性,以避免某一特性在其他方面占优势。分组标准可以由算法的代价函数或通过使用邻近度量允许聚类的另一标准来表示。
模糊C均值(FCM)算法相当于硬C均值(HCM)算 法[19]。 即 对 于 一 组 数 据 xi∈Rn,i=1,...,n,算法将n个元素分组。算法将元素分组成一个元素属于不同级别的不同组的集群。该算法的基本目标是找出组c中最有代表性的元素pj,它们将代表每个组或分区的中心。这些元素被迭代的最小化函数为式(11),考虑到μj(xj)的值表示分组的元素xi属于 j组和簇 pj。FCM算法的目标函数如下所示:
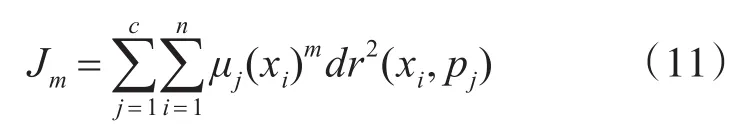
其中,c为簇的数目,n为可用数据的数量,m为模糊化因子确定模糊集的重叠度,dr是确定xi和 pj之间的距离度量。在本文中,使用欧几里德距离[20]作为邻近度量。需要注意的是系统中不同节点的有功或无功需求。
FCM算法执行以下算法来确定最小化的中心值和隶属度值Jm:
步骤1:计算满足以下关系的隶属度值μj(xi):

步骤2:计算聚类中心簇:
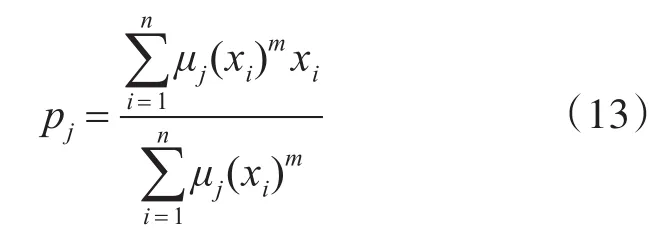
步骤3:更新每一个聚类中心簇的隶属度值:
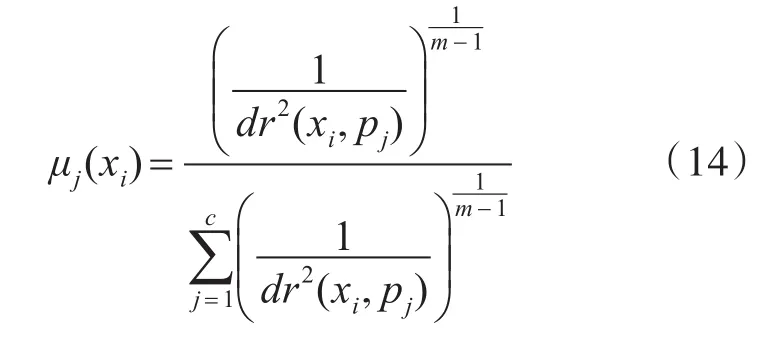
步骤4:循环步骤2和步骤3直至式(11)中的函数Jm满足最小收敛迭代。
FCM算法的一个难点是确定簇c的个数,一个不适当的选择可能产生不利用的 pj,j=1,...,c。解决这个问题的一种方法是使用验证索引,以允许其对由算法确定的分区或集群进行比较。
一个分区的质量或组的数量根据两个标准来评估[21]:压缩和分离。压缩确定每个组的成员应该尽可能接近彼此,可以通过最小化组的方差来实现。另一方面,分离确立了群体应该被充分分离在他们中间。
由一个验证函数组成,决定了一个分区的分离和压缩。提出的策略函数IS如下:
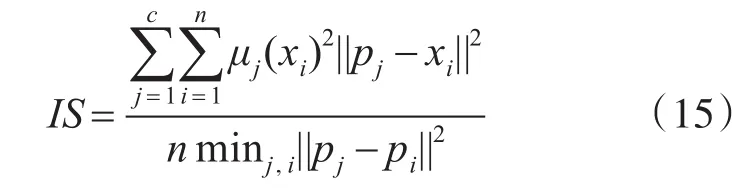
上面的函数与用于建立分区的算法无关。然而,如果FCM算法被应用于欧几里得距离,则可以给出以下关系:

其中,drmin为元素xi和簇 pj之间的最小距离。最好的分区是通过最小化来找到的,它提供了满足压缩和分离标准的分区。
运用FCM算法解决了不同簇c对元素xi的分区(即中心和隶属函数);如果每个值的值被评估,那么最好的分组应该满足Xie-Beni指数[22]最小值的标准,即 m in2≤c≤n-1Ωc。具体的算法如下所示:
步骤1:初始值 c=2,IS*=∞,c*=1;
步骤2:初始隶属度值 μj(xi)满足式(12);
步骤3:执行FCM算法;
步骤4:计算Xie-Beni指数 IS;
步骤5:如果 IS<IS*,c=c*,即没有找到最优解,则返回步骤2;
步骤6:如果簇c达到极限值,则停止迭代,否则进行步骤7;
步骤7:c=c+1返回步骤2,直至c=n/3。
3.3 配电网重构
利用神经网络方法的配电系统重构问题可以看作是一种模式识别问题,其中每种负荷模式都有一个最小损耗的拓扑结构。训练集应提供足够的信息,以便神经网络能够提供足够的问题映射,训练集的构造也应该与系统大小无关,以使神经网络适用于实际分布系统。
系统的状态是由每个系统总线上的有功和无功需求的向量来描述的。因此,对于每个系统状态,可能存在一个或几个径向拓扑和最小化目标函数。训练对由总线上的负载(输入数据)和最小化损失(输出数据)的拓扑构成。式(8)中的一对训练集i给出了系统状态的输入Ii,以及所需输出Di的最小化损失拓扑。
如果系统中的n个总线被分组到ms负载类中,则状态总数为 pms,四个离散级别导致64个状态。这些以二进制形式编码的状态将作为经典训练集参考的训练集。负载组由总线上的负载表示,它们具有类似的行为,不依赖于它们连接到的馈线。属于特定负荷级的组所有母线的负荷可以绘制如图2所示。
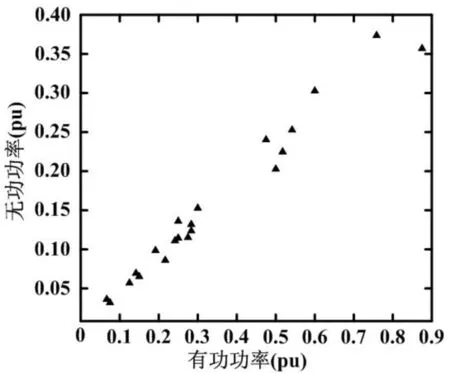
图2 负载组的有功功率和无功功率
这些负荷值表示系统的状态向量的子向量。图2中可用的信息可以通过使用较小的有功和无功需求来压缩。如果有功和无功功率的值是一个FCM聚类算法的输入数据,输出所减少的有功和无功值组由图3中的星号代表。
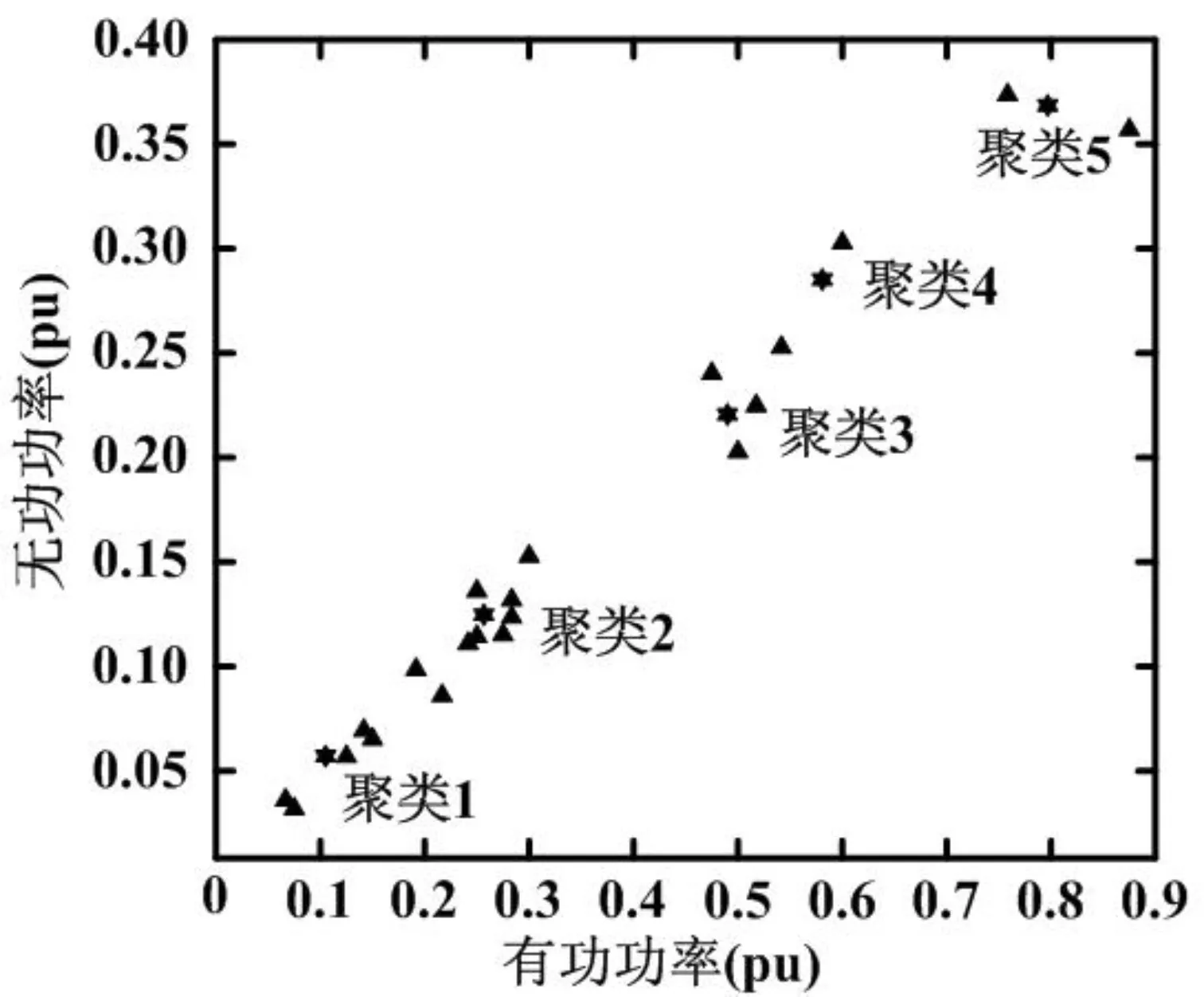
图3 FCM算法划分五个聚类代表负荷
一般来说,如果一个分布系统提出了三负荷组n1、n2和n3表示,则状态向量的大小为2(n1+n2+n3),其中负载在第1,2,3组上的子矢量的大小分别为2n1,2n2,2n3。如果使用聚类技术,由此产生的子矢量较小,这是由于对于第i组,ncgi组群数量低于 ni(即 ncg1<n1,ncg2<n2,ncg3<n3。向量如图 4所示,其中 n1≠n2≠n3,同样,ncg1≠ncg2≠ncg3)。
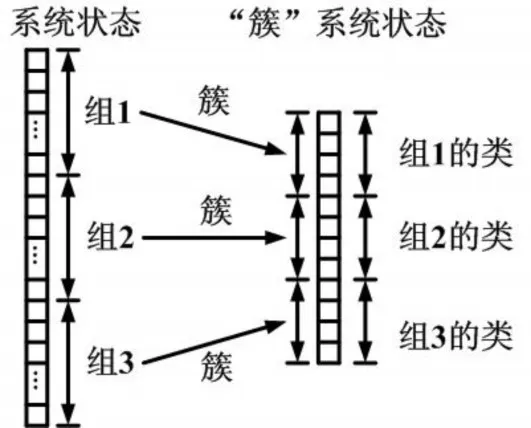
图4 利用聚类技术减少系统状态的大小
集群的数量由聚类技术应用于每个负载组策略所确定。对所有组重复该过程,以获得系统状态的最佳分区。这一过程概述如下。
1)建立经典训练集;
2)利用聚类技术定义每个加载组的分区数;
3)计算出有功和无功负荷组与FCM算法的功率值。
上面的策略减少了训练集输入向量的大小。因此,在输入层中神经元数目减少的情况下,用神经网络表示总线分布系统。如果不采用聚类技术,输入层会出现神经元,导致大系统分辨率的复杂化。因此,通过使用聚类技术,所需的输入神经元数量是集群数量的两倍。每个分析操作状态的神经网络的输出代表径向拓扑,最大限度地减少损失。为了建立具有径向拓扑的训练集,采用有两种方法可以确定输出中神经元的个数:1)输出神经元的数目与系统中分支的数目相同;2)输出神经元的数目与径向拓扑数相同。第一个方案可增强算法的泛化,因为它为系统提供任何径向拓扑。即所使用的神经网络结构如图5所示。
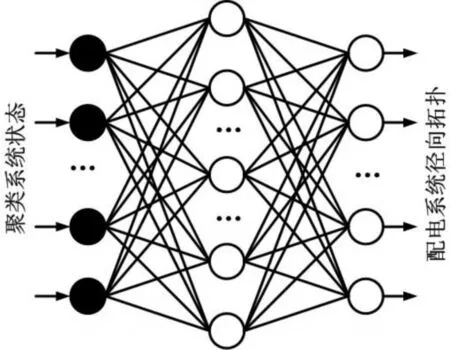
图5 神经网络结构
4 实验分析
运用两个系统来测试本研究所提出的方法:14节点配电网系统和136节点配电网系统。
4.1 14节点系统
系统数据采用文献[23]中实验数据,并将负载分为三组(住宅、商业、工业)。载荷进一步离散成四个级别(100%、85%、70%和50%),导致64个状态。对于统一地区采用相同的径向拓扑结构,利用重组器最大限度地减少系统的损失。
通过搜索c=2到c=n/3加载组来找到集群的数量。由于很少有加载总线,所以选择了c=3作为的最大值。该指标是利用本研究结合的聚类技术Xie-Beni算法与模糊参数m=2计算得出。结果如表1所示。
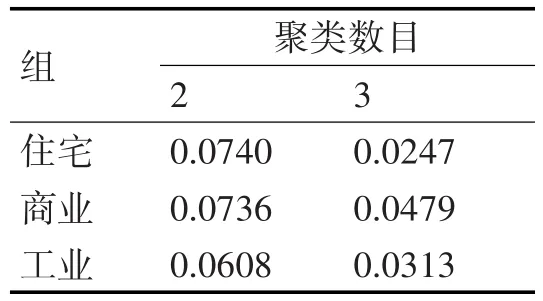
表1 14节点系统的验证指数
在表1中,通过式(16)计算出最好的聚类数目为c=3。同时,c=2也表现出较好的聚类结果。出于这个原因,这个参数也是用于实验的仿真过程。输入向量的大小减少了46.5%,因为26个元素(代表每个总线的两个数据的13个总线)减少到12个元素,代表了两个负载中心的三个集群中的每一个,有两个元素(有功和无功需求)。下一步是找到64个状态的聚类中心,并确定训练集。
神经网络提出了12个输入神经元对应的训练向量的尺寸,20个神经元的隐藏层和七个神经元的输出的结构,这代表了不同的拓扑结构发现的数量。隐藏层的传递函数为输出函数的线性函数。算法在训练阶段完成四个方面:1)自适应速率反向传播(bp-ra);2)传统的 Polak-Ribiere共轭梯度(cg-pr)指数;3)弹性反向传播(RBP);4)共轭梯度(CG)。对64个状态中的54个状态进行训练。神经网络泛化能力通过30个状态验证,其中10个来自训练集,10个为已知情况,但不属于训练集,再随机生成10个状态。神经网络的训练结果如表2所示。
由表2可见,给出了达到公差tol=0.0001的迭代总数,效率列显示了NN训练案例的百分比。其余的列显示了用于验证泛化能力的30种情况下的神经网络的性能。
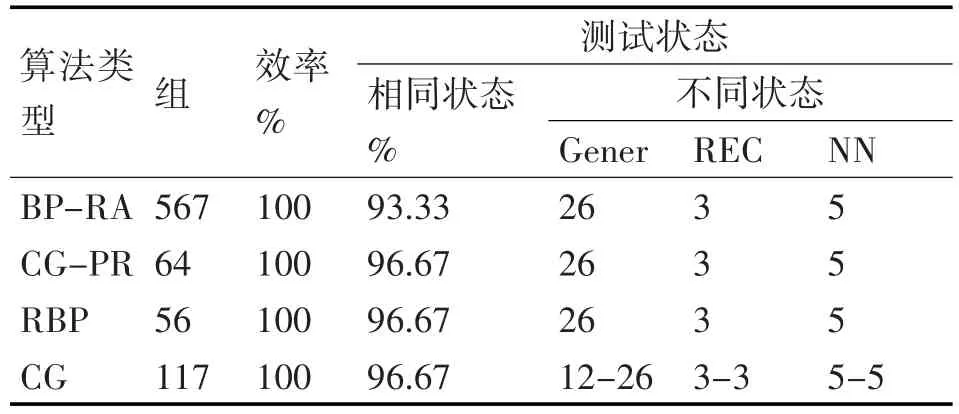
表2 12-20-7型神经网络训练结果
神经网络与RBP算法在30种状态下的29种状态相同,可用于验证重构算法。因此,表2所示的结果表明,用于训练阶段的所有算法的效率为100%。在泛化阶段,其他三种算法的效率为96.67%。需要注意的是神经网络算法提供了次优的拓扑结构,也降低功耗。
对于12-20-16型神经网络拓扑结构,与以前NN算法的唯一区别在于输出层中有16个神经元(系统中分支的数目)。这个系统的结果在表3两列进行了补充:循环和孤岛,这是不可行的拓扑结构和总线拓扑环孤岛的数量。在训练阶段和推广阶段有100%的效率。与此算法相比具有较低的处理时间,这使得该方法可用于现实环境中。
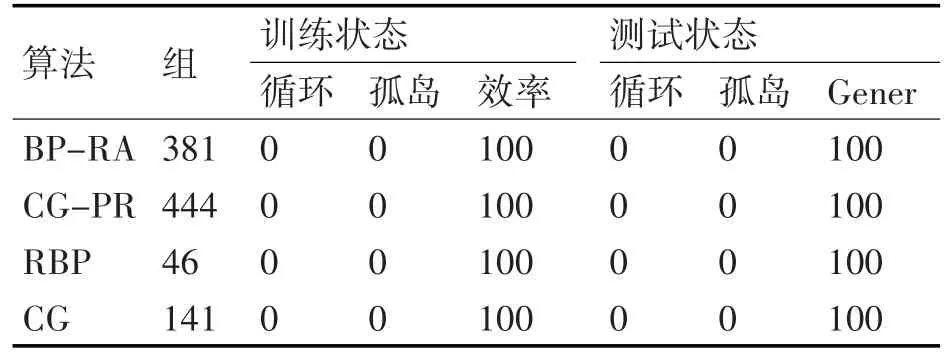
表3 12-20-16型神经网络训练结果
4.2 136节点系统
136节点系统采用文献[24]中实验数据,负载与前面14节点系统的分类和离散相类似,用于创建训练集的64种状态。为了减小输入向量的大小,找到三组(住宅、商业、工业)中负载组的最佳簇数。结果如图6~图8所示。在这个图中,计算的是不同的负荷中心。
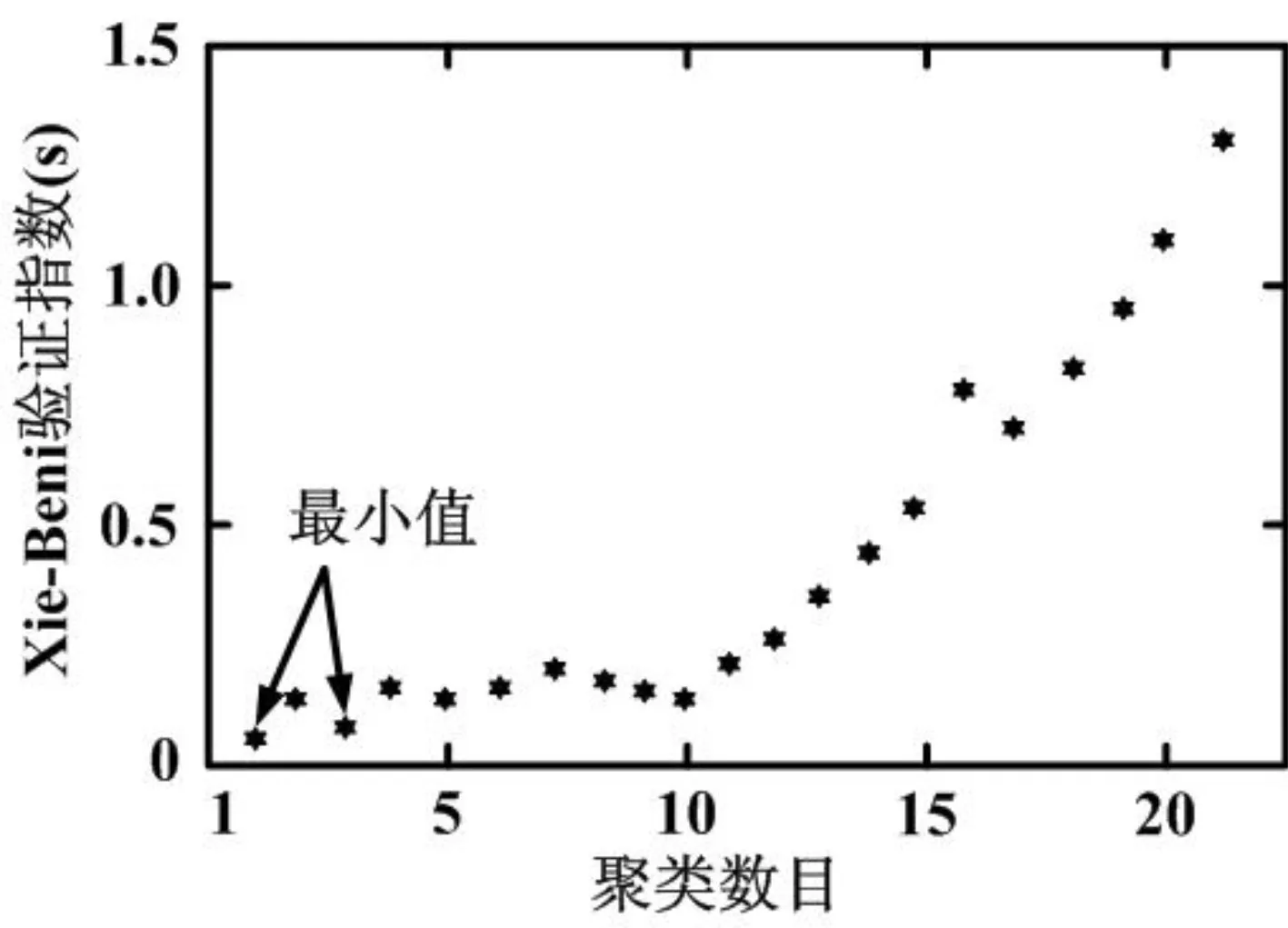
图6 住宅区域的聚类数目
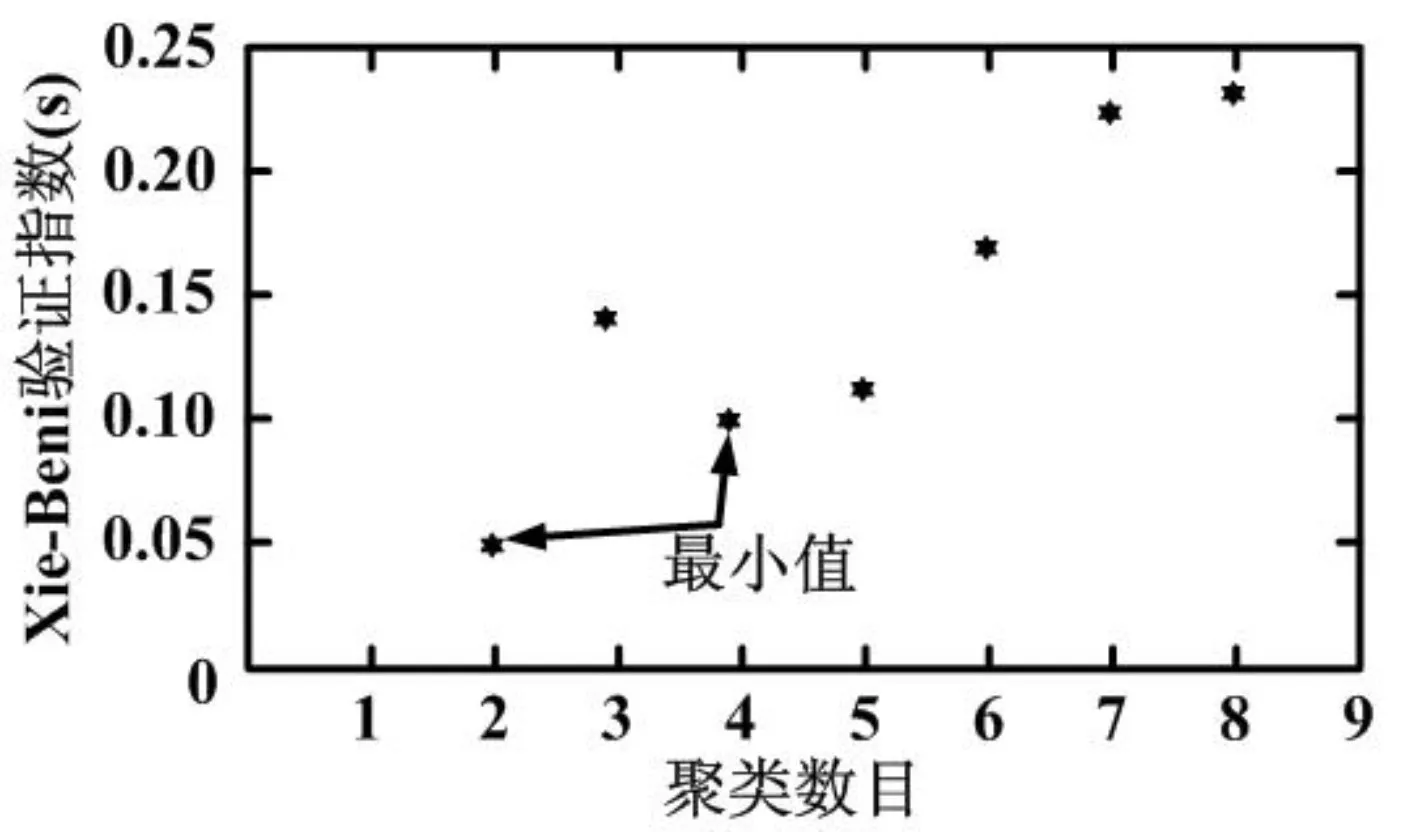
图7 商业区域的聚类数目
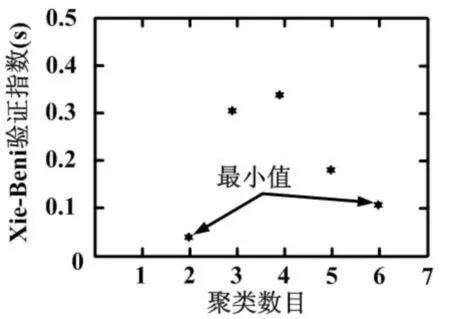
图8 工业区域的聚类数据
最好的簇数是由IS的最小值决定。对于这个系统,它是一个包含28个元素的向量。在这种情况下,根据集群技术,住宅和商业的四种负荷和工业的六种负荷是最有代表性的负荷(图6和图7)产生28个元素的向量。集群技术提供的输入向量的大小从272到28个元素有了显著地下降,对于136节点系统,有2×136个有功和无功功率数据,从而减少了89%输入向量的大小。
28-150-156型神经网络采用隐藏层的传递函数和输出层的线性传递函数。神经网络的训练与BP-RA算法和RBP算法相比,两者都表现出更快的收敛性,并采用了提前停止准则来提高泛化。本组实验中的64个状态作为训练集,随机生成40个状态,以分析泛化能力为目标。结果见表4和表5。
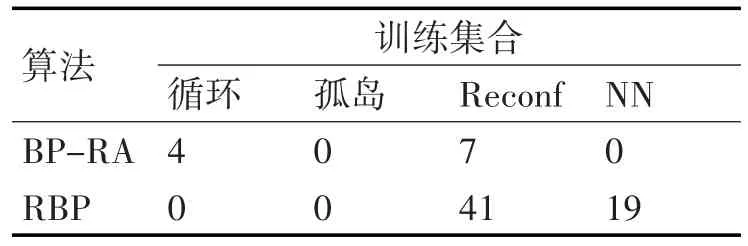
表4 28-150-156型神经网络训练阶段的结果
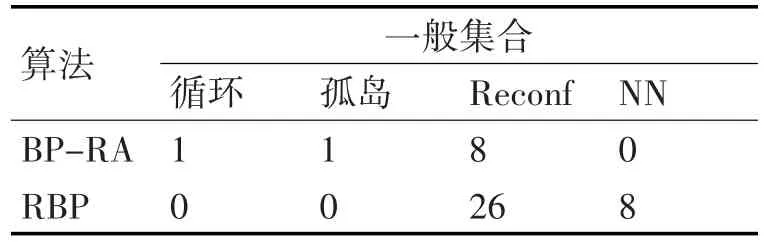
表5 28-150-156型神经网络训练泛化的结果
由表4和表5可见,BP-RA算法生成拓扑的训练阶段和两在泛化阶段。因此,该算法提供了最好的性能。生成的所有拓扑都是径向的。此外,神经网络提供了19个径向拓扑结构,其质量比标准重构算法在泛化阶段发现的要好。
5 结语
本文验证了神经网络求解实际系统的配电网系统重构问题的可行性。结合聚类技术减少了训练集的构建,但保留了足够的数据信息以提供给神经网络的进行计算。同时,使用了不同的算法与本文的神经网络算法相比较,对于处理相同的问题,所提出的结合聚类技术的神经网络算法比传统的神经网络算法具有更好的性能。最后,神经网络的处理时间非常低,使得这种方法适用于配电网系统的在线应用,如配电系统恢复问题。

