多粒度犹豫模糊粗糙集*

傅 凡 鞠恒荣

（1.江苏省光电子技术中心 镇江 212000）（2.南京大学工程管理学院 南京 210093）

1 引言

粗糙集理论［1］自著名的波兰教授Pawlak提出后已被广泛应用于模式识别、知识发现、决策支持、机器学习等众多研究领域［2～3］。

经典的Pawlak粗糙集模型建立在不可分辨关系的基础上，仅能处理名义型或离散型数据。而对于连续型数据则显得力不从心。为了解决这一问题，Dubois等将Zadeh的模糊理论与粗糙集理论相结合提出了模糊粗糙集方法和粗糙模糊集方法。该结合取得了巨大的成功，众多学者在此方向展开了许多富有成效的研究。2009年～2010年，文献［4］提出了犹豫模糊集（hesitant fuzzy set）的概念。2013年文献［5］提出了犹豫模糊粗糙集的构造性与公理化方法，第一次将犹豫模糊集与粗糙集理论融合进行了研究。

值得注意的是，Yang等提出的犹豫模糊集仍然只基于某一犹豫模糊二元关系，并不能处理多源信息系统等并行的数据。文献［6～11］认为在决策分析问题中，多个决策者之间的关系有可能是相互独立的［12～17］，因而需采用多个二元关系来进行目标的近似逼近，为此他提出了多粒度粗糙集的概念，并取得了丰富的成果［18～20］。

本文将犹豫模糊粗糙集与多粒度方法紧密结合，提出了多粒度犹豫模糊粗糙集模型，提出了乐观形式并研究该粗糙集模型的相关性质。研究表明本文提出的多粒度犹豫模糊粗糙集模型是清晰环境下的犹豫模糊粗糙集的有效拓展，同时，在一定程度上依然保有传统模糊多粒度粗糙集的相关性质。

2 预备知识

2.1 犹豫粗糙集

定义1［4］令U为讨论的论域，论域U上的犹豫模糊集可定义为

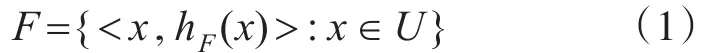
其中hF(x)为区间［0，1］上的集合，表示任意对象x∈U相对于F的隶属度。为了方便起见，hF(x)被称为犹豫模糊元素。

假设U为论域，那么U上的所有犹豫模糊集的集合可表示为HF（U）。与经典模糊集理论类似，可得到如下三个运算，见定义2。

定义2［4］令U为论域，∀F ，G∈HF(U)，可知

1）F的补集可表示为Fc，并且，

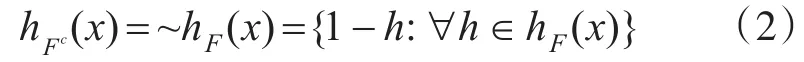
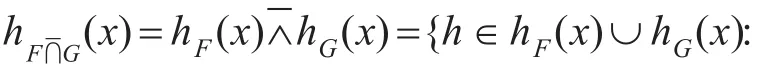
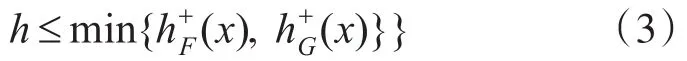
3）F和 G的并集可表示为 F-∪G，并且，

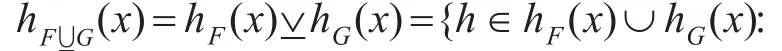
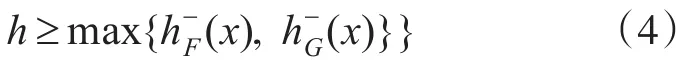
其中 h+F（x）和 h-F（x）表示犹豫模糊元素hF（x）的上界和下界，即：，。

定义3［5］令U为论域，∀F ，G∈HF（U），假设对于任意的，即（x）且，那么F即为G的子集，可表示为或。此外，假设并且存在使得或，那么F即为G的真子集并表示为。

由定义3可得到如下定理。

定理1［5］令U为论域，，，可得

定理2［5］令 U为论域，假设hF（x）和 hG（y）为两个犹豫模糊元素，对于，，可得

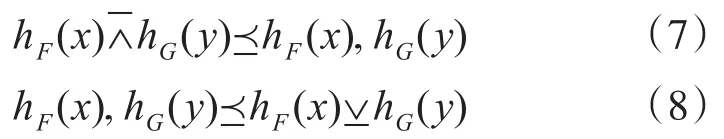
根据如上讨论，可将Pawlak模糊集扩展到犹豫模糊环境中。令U为论域，ℜ为一族犹豫模糊关系，那么HK=（U，ℜ）为犹豫模糊知识基，，HAP=（U，ℜ）表示犹豫近似空间。根据Yang等人的讨论，犹豫模糊粗糙集可定义如下。

定义4［5］令U为论域，ℜ为U的犹豫模糊关系，，下近似集与上近似集可分别表示为和，且，

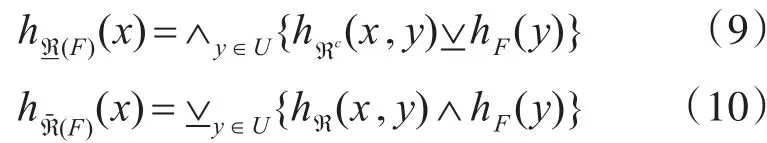
2.2 多粒度粗糙集

在经典粗糙集模型中，目标有且仅用一个二元关系近似逼近，为了满足现实生活中分布式数据的处理，Qian等提出了多粒度粗糙集，该粗糙集由一族二元关系来近似逼近目标。Qian等的粗糙集模型由两种不同的形式构成，分别是乐观多粒度粗糙集模型和悲观多粒度粗糙集模型。本文仅介绍乐观多粒度粗糙集模型。

定义5［6］令S为一信息系统，，对于，X的多粒度乐观下近似集合与多粒度乐观上近似集合可分别定义为

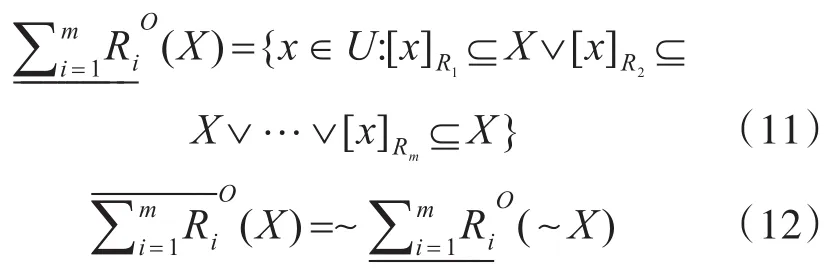
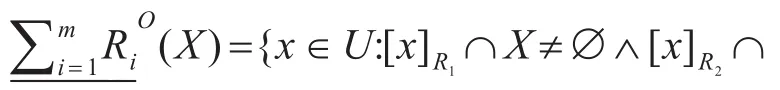
3 乐观多粒度犹豫模糊粗糙集的定义

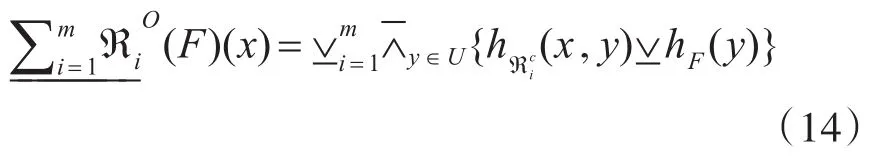
4 乐观多粒度犹豫模糊粗糙集的性质

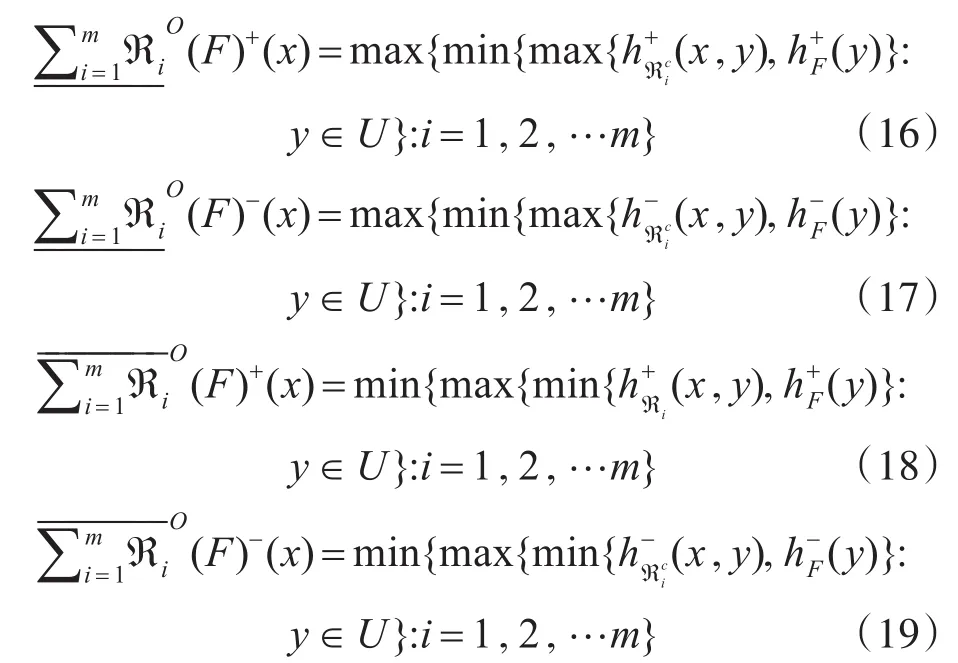
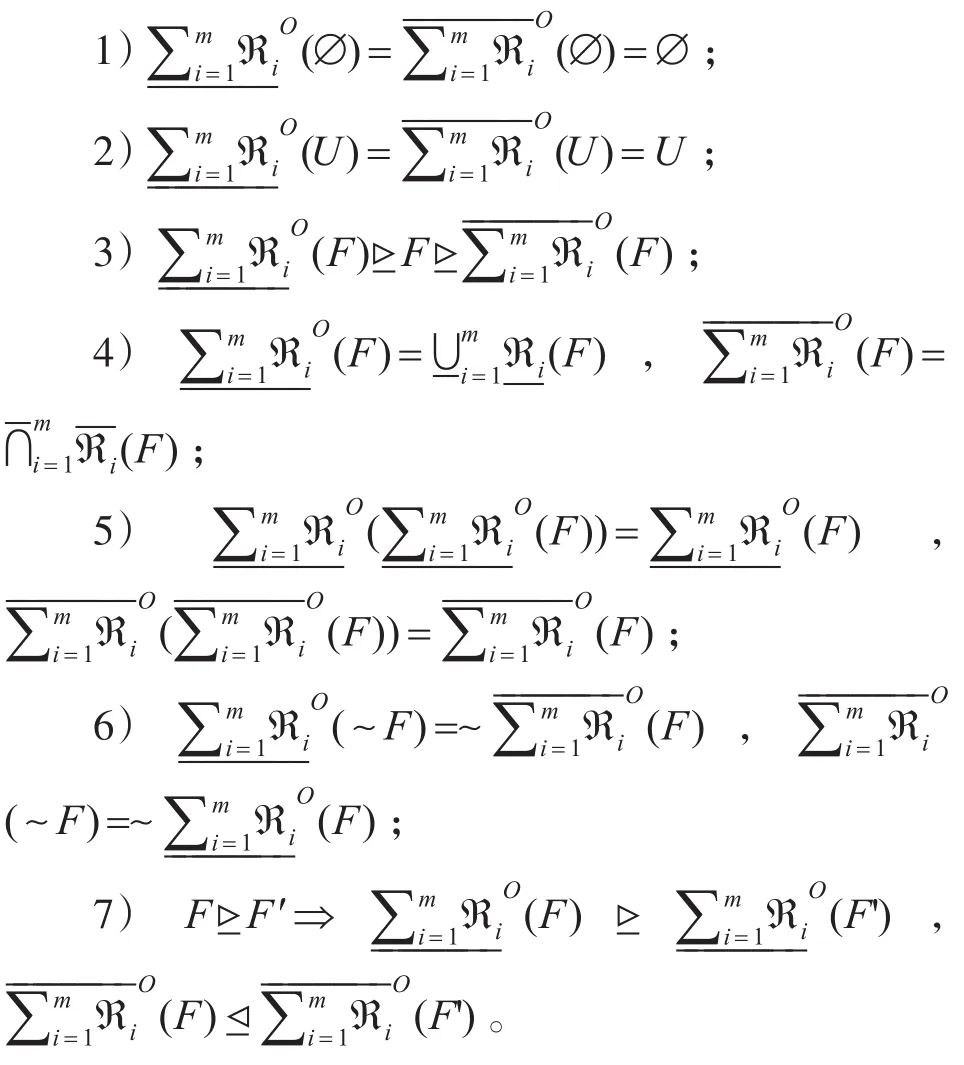
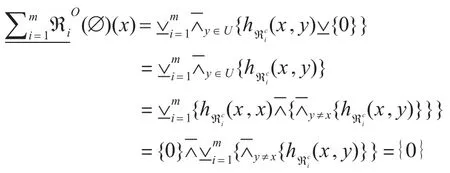
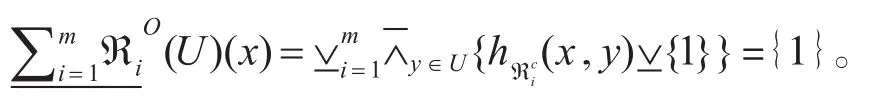
3）∀x∈U ，根据式（16）可得

∀x∈U ，根据式（17）可得?

4）∀x∈U ，

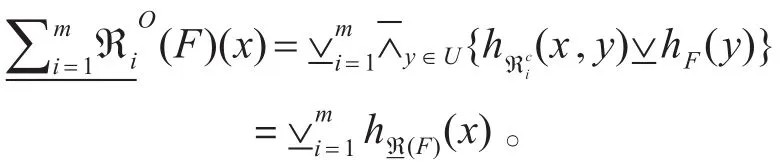
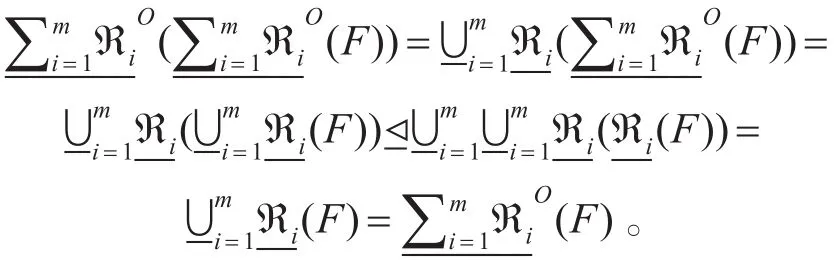
6）∀x∈U ，

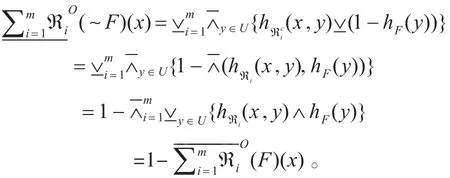
证明：1）∀x∈U ，

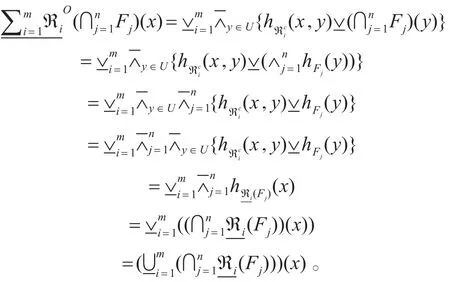
2）∀x∈U ，

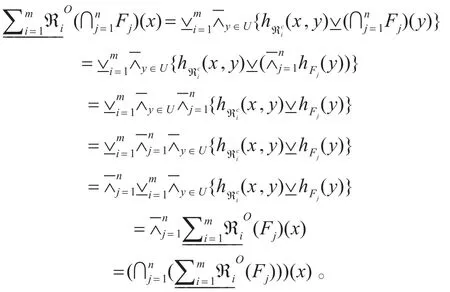
5 结语

本文将多粒度思想引入犹豫模糊粗糙集模型中，提出了乐观多粒度犹豫模糊粗糙集模型，分析了其相关性质，并从理论上证明出本文提出的多粒度犹豫模糊粗糙集模型是经典多粒度粗糙集模型和经典犹豫模糊粗糙集模型的进一步泛化，更能满足实际工程的需要。下一步将研究多粒度犹豫模糊粗糙集的约简和规则提取工作。