基于SVM 的放气活门调节模型多元回归分析

曹惠玲，王 新

（中国民航大学航空工程学院，天津 300300）

基于SVM 的放气活门调节模型多元回归分析

曹惠玲，王 新

（中国民航大学航空工程学院，天津 300300）

航空发动机2.5级放气活门是重要的防喘机构。本研究针对轴流式压气机喘振机理进行分析，使用支持向量机（SVM，support vector machine）方法，通过对 PW4077D发动机 30个无故障航班 QAR（quick access recorder）数据的处理与多元回归分析，分别建立了3个航段下2.5级放气活门的辨识模型。随机选取一次航班的QAR数据，使用已建立的模型对一次航班的2.5级放气活门开度进行计算并与实际开度值进行对比，验证了通过回归分析得到的辨识模型具有较高的准确度，对于航空发动机状态监控和故障诊断具有一定的应用价值。

支持向量机；回归分析；辨识模型；QAR；PW4077D；2.5级放气活门

?

航空发动机的稳定运行与飞机的飞行安全息息相关。压气机喘振是气流沿压气机轴线方向发生的低频率、高振幅的振荡现象，其能够导致发动机机件的强烈机械振动和热端超温，并在很短的时间内造成机件的严重损坏，使压气机叶片断裂，引起发动机熄火停车，严重威胁发动机安全工作和飞机的安全运行。因此应尽力避免发动机喘振的发生。

多级轴流式压气机中间级放气可有效提高压气机的喘振裕度，避免喘振现象的发生，是现有民用航空发动机防止喘振的重要机构。

但在飞机运行过程中，由于放气活门作动频繁，容易出现打不开、关不严、打开角度不合理、打开或关闭过程卡阻的现象。如果在关键时刻起不到应有的防喘作用，则很容易造成发动机喘振的现象，给飞行安全造成威胁。

根据航空发动机喘振基本原理，利用基于统计学理论的支持向量机方法，对大量QAR数据进行回归分析，建立放气活门系统的辨识模型，可实现对活门开度的准确预测，为预防和排除故障提供充分时间和决策依据，对于有效实施航空发动机的视情维修决策、提高飞机发动机运行安全性具有指导意义。

1 基于支持向量机的系统辨识原理

发动机模型的建立主要有机理模型和辨识模型两种。

机理建模是基于部件特性和气动热力学等原理推导得出对系统进行描述的数学模型，这类建模也叫做白箱建模。

系统辨识是一种利用系统的输入输出参数，构造一个相对真实的反映客观对象数学模型的方法，是黑箱建模问题，即使对系统的结构和参数一无所知，也可通过系统的输入和输出参数来求得系统模型，是对实际系统一个合适的近似[1]。建立放气活门模型的问题可以转换为对放气活门开度值的回归问题，利用支持向量机回归（SVR）分析方法非线性函数任意逼近的特点，可在一定程度上对复杂的非线性系统进行辨识。

1.1 理论基础

支持向量机是Cortes和Vapnik于1995年提出的。SVM方法是建立在统计学习理论的VC维理论和结构风险最小原理基础上的，根据有限的样本信息在模型的复杂性（即对特定训练样本的学习精度）和学习能力（即无错误地识别任意样本的能力）之间寻求最佳折衷（即结构风险最小），以期获得最好的推广能力（或称泛化能力）[2]。并且能够推广应用到函数拟合等其他机器学习问题中。

SVM理论来自对数据分类问题的处理，最初用于线性可分的二分类算法。

图1为二维空间R2上的分类问题，其训练集由两类点组成，希望构造一条分划直线l1：ωx+b=0，其中ω为超平面的法向量，b为超平面的偏移量，能将两类点正确地分开。通过平行的向左右平移直线l1，直至碰到一个训练点。这样得到2条直线l2和l3，这2条直线称为支持直线。当2条支持直线l2和l3的间隔最大时，直线l1对两类样本的区分能力最佳。根据上述思想就把寻求分划直线l1：ωx+b=0问题转化为对ω和b的最优化问题。

图1 支持向量机最优分类超平面Fig.1 SVM optim al classification hyperplane

对于回归问题，是通过把其转化为分类问题而解决的。考虑一维空间R上的线性回归问题，如图2所示。

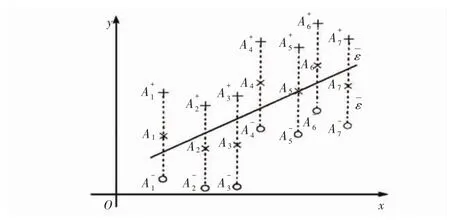
图2 支持向量机处理回归问题原理示意图Fig.2 Principlediagram of SVM dealing with regression prob lem

通过将训练集T中每个训练点的y值分别增加ε和减少ε，得到正类点和负类点两个集合，分别记它们为D+和D-，由此得到分类问题的训练集。然后对上述训练集进行一次完全正确的线性分划。使所有训练点都应在回归直线的ε带之内，要寻求的回归直线应该是满足上述条件的斜率最小的那条直线。即用下列方式寻求回归直线：考虑能够盖住所有“×”形训练点的竖直方向长度为2ε的条形带，从这些条形带中选出最接近水平的条形带，然后选取恰好位于该条形带中间那条直线作为回归直线。以上便是支持向量机的基本原理。

对于线性不可分的情况，通过引入形如公式X=Φ（x）的非线性映射，将输入数据映射到一个高维特征空间，使训练数据实现超平面的分割。用核函数K替代变换 Φ，并用核函数值 K（·，·）替代内积 Φ（·）·Φ（·），简化了内积的计算，同时十分巧妙地实现了从线性到非线性划分的过渡。

1.2 数学描述

支持向量机回归（SVR）算法可归结如下：给定训练集

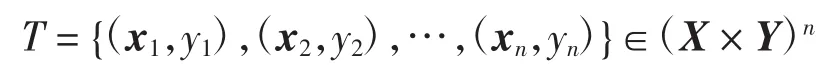
其中：xi∈X=Rn；yi∈Y=R，i=1，…，n。

用函数f（x）=ωx+b拟合观测样本的支持向量机回归分析可表示如下

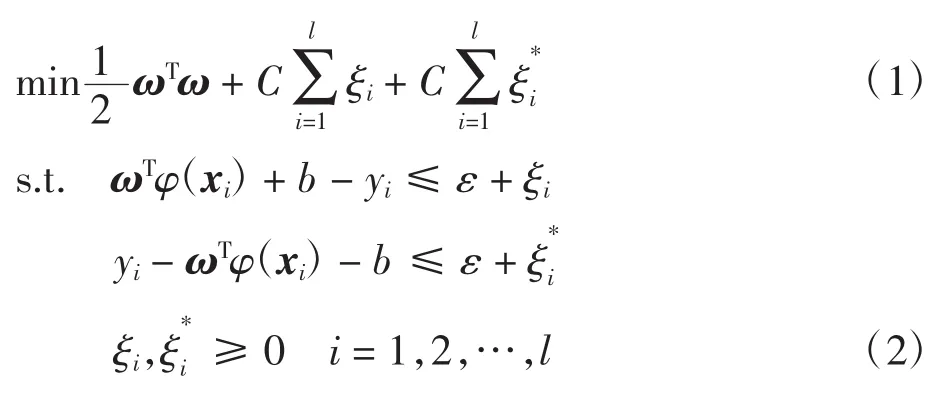
其中：xi为输入向量；ω∈Rn为权值变量；C为惩罚系数，控制对超出误差的样本的惩罚程度；ε为不敏感损失函数，其值影响支持向量的数目；ξi、ξ*i为松弛变量，表示样本偏离ε的程度。对于式（1）和式（2），一般通过求解上述模型的拉格朗日方程的对偶问题获得原问题的最优解

其中：K（xi，x）称为核函数；αi和 α*i为拉格朗日乘子。

核函数可以看作一个特征提取的过程[3]，选择正确的核函数有助于提高分类准确率。高斯核函数通过调控参数σ具有相当高的灵活性，也是使用最广泛的核函数之一。本文采用高斯径向基核函数（RBF，radial basis function），即

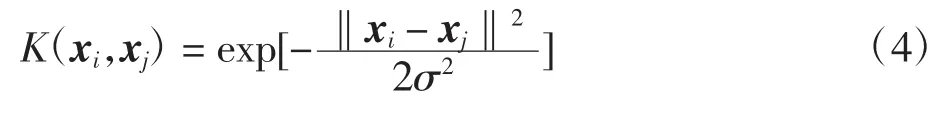
2 喘振机理及回归模型分析

轴流式压气机喘振的发生主要是由于气流分离引起的。压气机工作时，气流进入叶片的流入角为β，一般情况下与叶片的几何进口角βk不一致，其差值称为攻角。在设计工作状态下，轴流式压气机各级通道截面变化符合空气容积流量变化的需要，气流攻角较小，空气能够无撞击地流入各级压气机叶栅，因而各级叶栅不会发生气流分离现象[4]。

但在压气机的工作范围内，攻角变化很大，从速度三角形（如图3和图4所示）可以得到攻角

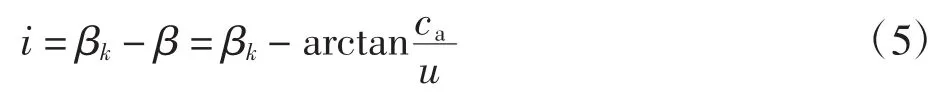
其中：i为攻角；ca为气流轴向速度；u为叶片旋转切向速度。

图3 叶盆分离Fig.3 Bladebasin separation

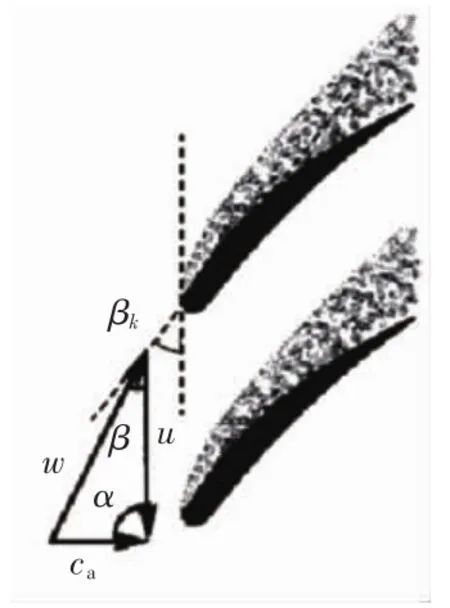
图4 叶背分离Fig.4 Bladeback separation

当压气机转速一定时，如果压气机空气流量增加，使气流轴向速度ca上升，攻角i下降，甚至为负值，当负值过大，就会发生叶盆分离，如图3所示。叶盆分离降低了叶片工作效率，但该涡流区不会继续扩大。

当压气机转速一定时，如果压气机空气流量减小，使气流轴向速度ca减小，攻角i增大。当攻角过大时气流从叶背分离，如图4所示，称为失速，失速会导致压气机效率显著下降。当失速现象进一步发展时，会使压气机整个通道气流受阻，甚至使压气机进入喘振状态。

压气机中间级放气活门是一种结构简单有效的防喘机构。当压气机转速低于一定数值时放气活门打开，并根据不同的发动机状态，放气活门打开特定的角度，控制放出空气的量[5]，使流量系数维持在一个合理范围内，即使前级攻角不要太大，避免产生叶背气流分离，也不要放出过多压缩空气，降低机械效率。

通过对速度三角形的分析可知，压气机喘振的主要影响因素是发动机叶片的切线速度与压气机进口流量。低压压气机转速N1直接决定叶片切线速度，并且根据双轴发动机转速特性可知，转速N1对低压压气机进口流量也有直接影响。PW4077D发动机在低压压气机出口处设置了2.5级放气活门，在QAR数据中用SELBP25表示。通过相关性分析可以得到N1与SELBP25的相关系数高达-0.968。因此在建立2.5级放气活门回归模型时选择N1作为模型的输入参数。根据空气动力学原理，压气机进口流量还受进口总温、总压的影响，建立辨识模型还选择作为模型的输入参数。

2.5级放气活门的开度控制不仅要考虑低压压气机的工作状态，还需考虑与高压压气机的流量匹配情况，避免放气量过大或过小使高压压气机发生气流分离的现象。因此在建立2.5级放气活门开度模型时，选择能够影响高压压气机进口流量的参数P2.5、T2.5、N2、VSV开度作为模型的输入[6]。

在反推段，由于反推活门的打开，改变了发动机气路，因此在建立反推段放气活门开度模型时增加反推活门开度TRA作为模型输入参数。本文选择2.5级放气活门位置反馈参数SELBP25作为模型的输出参数。

一次航班的飞行过程可分为地面滑行、起飞、爬升、巡航、下降、进近和反推着陆7个阶段。本文选取了PW 4077D发动机的一次典型正常航班数据，在该航班飞行全过程中，2.5级放气活门开度状态如图5～图7所示。

图5 一次正常航班起飞前地面滑行及起飞段放气活门开度调节Fig.5 VBV opening modulation in a norm al flight’s taxiing and taking-off segment

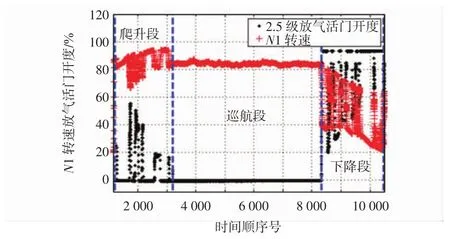
图6 一次正常航班爬升、巡航和下降段放气活门开度调节Fig.6 VBV opening modulation in a norm al flight’s clim bing，cruise and descendent segment

图7 一次正常航班进近、反推着陆和地面滑行段放气活门开度调节Fig.7 VBV opening modulation in a norm al flight’s approaching，T/R and taxiing segment

从一次典型的正常航班全过程中2.5级放气活门调节图示中可看到，在地面滑行阶段，此时发动机转速较低，放气活门开度最大；在巡航阶段，放气活门开度为0。在以上两个航段中开度调节较少。在起飞、爬升、下降、进近、着陆反推航段，放气活门的开度调节频繁。2.5级放气活门的调节主要集中在这几个过程。

由于飞机在爬升段和下降段飞行时间较长，飞行高度变化较大，飞机经历的外界环境多样，放气活门的开度调节影响因素较复杂，较难建立准确的模型。相反，飞机在起飞段、进近段、反推着陆段发动机工作状态及工作环境变化相对简单。在飞机的加速起飞段，发动机处于最大推力工作状态；在进近段，发动机多处于慢加速和慢减速的连续调节状态；在反推段，由于反推活门的打开改变了发动机气路构型，是重要的影响因素。因此本文选择飞机的加速起飞段、进近段和反推着陆段分别建立多元回归模型。

3 基于支持向量机VBV模型辨识与应用

3.1 数据的预处理

1）发动机性能参数的标准化修正

由于模型训练样本取自30个航班QAR数据，为使不同航班间飞机的性能参数具有可比性，须转化到统一的飞行条件下进行比较。换算后参数用下标“cor”表示。发动机转速相似修正公式如下[7]

2）数据归一化

由于所选用的参数类型不同，造成每一种参数的数值变化范围差异较大。为了消除各参数不同量纲对模型训练的影响，本文采用线性归一化法，对各输入输出参数进行处理，归一化后数据将分布在[0，1]范围内。采用的线性归一化计算公式为

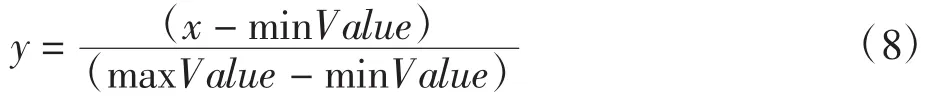
3）支持向量机参数的优化

支持向量机中惩罚系数C和RBF核函数中σ的选择，对支持向量机的回归效果有显著影响，其选取方法可采用网格算法、遗传算法和粒子群算法。本文采用网格法对二者进行寻优计算。

3.2 模型的建立与应用

基于上述数据处理过程，本文选取PW 4077D发动机30个航班相应航段的QAR数据作为训练数据，分别建立各航段2.5级放气活门开度控制模型。选取同型号发动机的一次航班QAR数据对模型准确性进行验证，即利用建立的模型对该航班中各航段放气活门开度进行计算，计算结果如图8～图13所示。

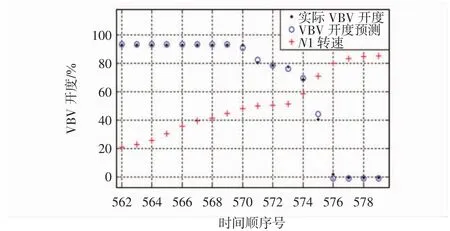
图8 加速起飞段2.5级放气活门开度预测结果对比Fig.8 Comparision between predicted opening of2.5 bleed valve and actual results in taking-off segment

图10 进近段2.5级放气活门开度预测结果对比Fig.10 Comparision between predicted opening of 2.5 bleed valve and actual results in approaching segment

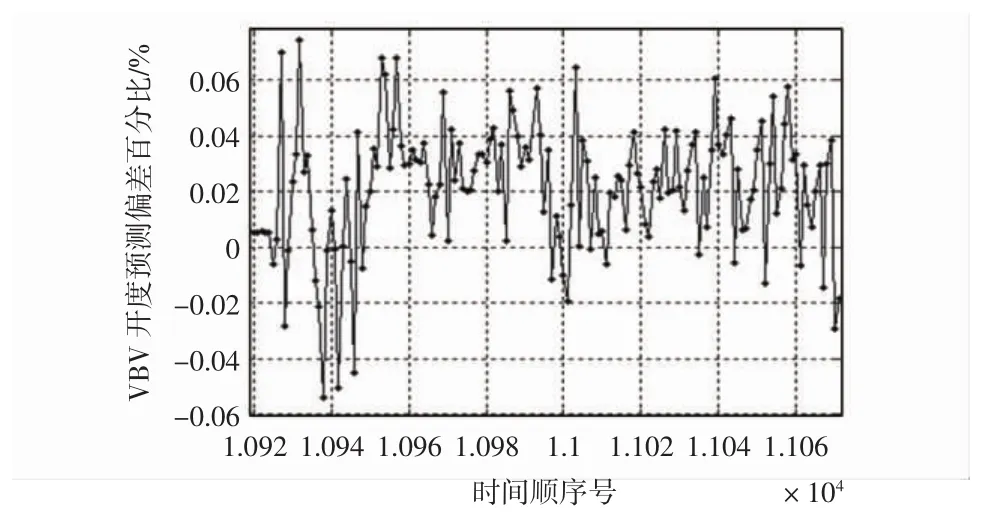
图11 进近段2.5级放气活门开度预测偏差百分比Fig.11 Prediction error percentage of 2.5 bleed valveopening in approaching segment

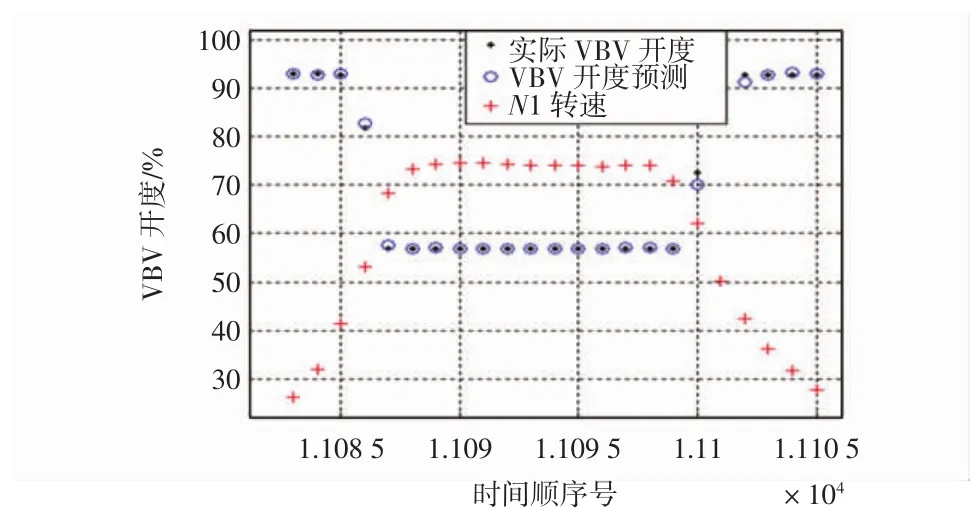
图12 反推段2.5级放气活门开度预测结果对比Fig.12 Comparision between predicted opening of 2.5 bleed valve opening and actual results in T/R segment

分析以上结果可见，模型计算的放气活门开度值非常接近实际开度值，放气活门回归模型开度计算最大偏差百分比在2%以内。尤其在反推段模型开度最大计算偏差百分比在0.05%以内，具有较高的预测精度，因此可以表明：文中采用的多元回归建模思路是可行的，所建立的模型能够较好地反映2.5级放气活门的控制规律，有助于研究人员了解国外先进发动机放气活门的控制规律；并且通过该模型计算结果与实际开度值的差异分析，可实现对发动机2.5级放气活门的状态监控，及时发现放气活门的开度异常；在维修人员分析发动机喘振及2.5级活门相关故障时可以提供指导作用。

4 结语

本文详细分析了支持向量机用于回归分析的理论基础，分航段建立了基于支持向量机回归的放气活门开度控制模型。使用飞机QAR数据中记录的状态参数，利用模型对2.5级放气活门开度进行计算，结果表明，模型计算结果与实际开度相比具有较高的准确度，表明利用支持向量机方法建立放气活门的辨识模型是可行的。有助于了解放气活门开度控制规律，对于发动机状态监控与故障诊断具有指导作用。由于航空发动机在整个飞行过程中，其运行状态复杂多变，外界环境变化较大，因此需要更加深入地研究飞机发动机的控制特点以及其它影响因素，从而得到更加完备的放气活门控制模型。

[1]李应红,尉询楷.航空发动机的智能诊断、建模与预测方法[M].北京:科学出版社,2013:103.

[2]阎 辉,张学工,李衍达.支持向量机与最小二乘法的关系研究[J].清华大学学报,2001,41(9):77-80.

[3]邓乃扬,田英杰.数据挖掘中的新方法——支持向量[M].北京:科学出版社,2004:151.

[4]丁蓬勃,王仲生.航空发动机喘振故障机理及监控方法研究[J].科学技术与工程,2010,10(15):1671-1815.

[5]Pratt&Whitney Company.Engine Health Monitoring Training Guide[Z].Pratt&Whitney Company,2005:8-24.

[6]CFMI Company.CFM56-7B Training Manual[Z].CFMI Company,2005:296-313.

[7]王 云.航空发动机原理[M].北京:北京航空航天大学出版社,2006:178-182.

Multiple regression analysis of bleed valve regulation model based on SVM

CAO Huiling,WANG Xin
（College of Aeronautical Engineering,CAUC,Tianjin 300300,China）

Aero engine’s2.5 bleed valve is an important mechanism to eliminate the risk of stall and surge.Stall and surge mechanism of axial-flow compressor are analyzed;after30 trouble-free flights’ QAR （quick access recorder）data analyzed and disposed,3 flight sections’identification models of2.5 bleed valve control models are setup by using SVM method.Applicating the models on a flight’s QAR data,the bleed valve opening is calculated and compared with the actual value,proving that the models have higher accuracy and certain application value in the condition monitoring and fault diagnosis of aero-engine.

SVM;regression analysis;identification model;QAR;PW4077D;2.5 bleed valve

曹惠玲（1962—），女，河北唐山人，教授，工学博士，研究方向为航空发动机性能分析与故障诊断.

V263.6

A

1674－5590（2017）05－0012－05

2016-11-23；

2017-02-20

中央高校基本科研业务费专项（3122014D010）

?

杨媛媛）