基于K 近邻模型的空中交通流量短期预测

赵元棣，陈俊夫，刘泽宇，盛受琼，白志建

（中国民航大学a.空中交通管理学院；b.理学院，天津 300300）

基于K 近邻模型的空中交通流量短期预测

赵元棣a，陈俊夫a，刘泽宇a，盛受琼b，白志建a

（中国民航大学a.空中交通管理学院；b.理学院，天津 300300）

为了准确预测空中交通短期流量，减轻空管协调压力，基于K近邻算法构建了空中交通短期预测模型。首先，通过多次取K值比较相对误差来确定合适的K值。之后，对原有的K近邻模型进行改进，引入空间参数，提出了3种状态向量组合的K近邻模型：时间维度模型、向台航路-时间维度模型与时空参数模型。以某扇区雷达数据对该模型进行检测，结果表明：同时引入时空参数的K近邻模型误差最小，平均为14.16%；基于指数权重的距离衡量方式均能达到预测精度优化的效果；高斯权重预测法在时间维度模型下优于反函数法，引入空间参数则反之；指数权重距离下的反函数法预测的时空参数模型误差为13.94%。改进后的K近邻模型对不同流量情况都具有普适性，预测结果可为空中交通流量管理提供理论参考。

空中短期流量预测；K近邻；状态向量；时空参数；高斯函数

?

随着民航事业的发展，空中交通流量不断增加，管制员的压力日渐增大，为了分担管制员决策压力，减轻管制员负担，智能化在民航系统表现出了良好的接受度和实用性，刘永欣等[1]提出建立基于管制员知识的空管智能交通辅助系统。

如今，智能交通系统研究的投入不断加大，交通管理也逐步走向实时化、准确化和信息化。与此同时，交通研究领域积累了大量历史数据，为交通管理者和研究人员提供了重要的数据支持。其中，短期交通预测中的K近邻算法在研究智能交通系统中的地位尤为突出，首先运用于公路交通领域。相对于参数回归算法，K近邻非参数回归算法无需建模，无需设置大量假设条件[2]。Smith[3]在Davis的研究基础上，采集了某条环形公路5个月的交通流量数据，将历史均值和相邻时段流量作为状态向量，测试了K近邻非参数回归算法。将预测结果与神经网络预测模型作对比，结果表明K近邻非参数预测算法的平均误差较小。

近年来，国内也开始对交通流量管理中的关键技术展开研究，并对K近邻法交通流预测问题进行了深入的研究与论证。翁剑成等[4]对快速路行程速度进行了预测；于滨等[5]通过引入时空参数与指数权重，从状态向量和距离衡量方式入手改进K近邻模型；谢红海等[6]用模式距离搜索方法代替原有的欧氏距离搜索方法，引入多元统计回归模型，建立了一种改进的短期交通流预测的K近邻算法。

随着地面相关研究的深入，空中模型预测的研究也渐渐受到重视。但国内运用K近邻法进行空中交通流量预测仍很鲜见，本文尝试将K近邻算法运用于空中交通领域，通过建立不同的状态向量以及改变预测算法，构建短期交通流预测模型，研究各时空参数和预测算法对预测精度的提高效果。通过采集某扇区真实雷达数据，对提出模型进行仿真验证。

1 K近邻预测模型

K近邻（K-nearestneighbor）非参数回归方法的核心思想是：取得一个尽量完备的历史数据库，用于提取数据特征，再根据现阶段的数据特征对比历史数据库中的历史数据，将与现阶段数据特征最相似的历史数据应用于未来情况预测。因而可通过数据特征从历史数据库中得到预测根据，事实证明K近邻非参数回归方法具有可移植性，从而得到广泛的应用[7]。

1.1 近邻数的选取

近邻个数K代表在历史数据库可寻得的最相似数据集数，可采用欧式距离等作为衡量方式，K值的选取与历史数据有关，目前尚无标准规则来规范K的选取，偏大或偏小都会影响预测的准确度。

1.2 状态向量的选取

状态向量作为现阶段实测数据与历史数据库实施匹配的一个匹配标准，表征了历史数据库中的数据特征。算法在搜索K个近邻时，需通过这些特征来匹配，状态向量就是这些数据特征的描述，其选取的合理与否很大程度上关系到预测精度。

1.3 距离衡量方式

距离衡量方式是为了体现现阶段实测数据与历史数据库中各组数据集的近似关系。一般采用欧式距离作为衡量标准，如

其中：di为现阶段实测数据与历史数据库中第i组数据的距离（该数据在本文算例中体现为航班架次）；xj为现阶段数据中第j个子数据的值；xji为第i组历史数据中第j个子数据的值；ωj为现阶段第j个实测数据的权重。

1.4 预测算法

预测算法构造了采用K组近邻数据集预测下一阶段数据值的方案，即

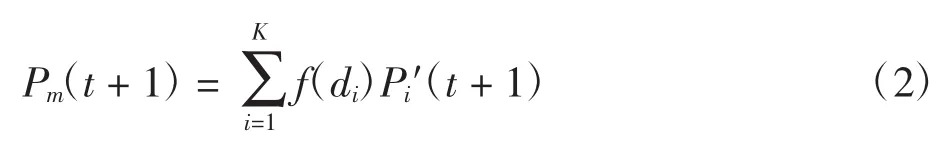
其中：di为现阶段实测数据与第i个近邻的距离；Pm（t+1）为第m个航路点第t+1时段的预测值；Pk′（t+1）为历史数据库中搜索到的第K个近邻所对应的第t+1时段的航班架次实测值；f（di）为第i个近邻所对应的权重。

1.5 误差评估方法

关于预测效果的评价，选用相对误差为

其中：P为算法预测航班架次值；M为历史数据库中与P对应的航班架次实测值。

2 短期预测模型的建立

借助原有的K近邻预测模型，并进行加强，反映在以下3个方面：①引入时间维度和空间维度来建立状态向量；②距离衡量方式中引入了权重系数；③考虑到反函数权重法为近邻赋以很大的权重，会使算法对噪声更敏感，故采用高斯函数模型进行对比。

2.1 不同K值的选取

K近邻算法中，K的选取对于预测模型的精度有较大影响，图1给出了不同K值下近邻选取的规则。若K值过小，该模型结果易受到噪声影响；反之，若K值太大，模型会因为纳入过多异常状态向量导致预测精度下降。

交叉验证是统计学上将训练数据分成较小子集合进行验证的使用方法[8]。利用交叉验证测试该短期空中交通预测模型泛化能力的好坏，并以此为依据选取K值。

2.2 基于时空参数的状态向量

每一个航路点都不独立存在于一个航路体系中。不管上一个航路点还是下一个航路点航班量剧烈增减，都必然会影响该航路点现阶段的航班量。基于该理念，构建3种时空参数的K近邻流量预测模型，如图2所示，分别为时间维度模型、向台航路-时间维度模型、时空维度模型。

图1 K值的选取Fig.1 Selection of K value

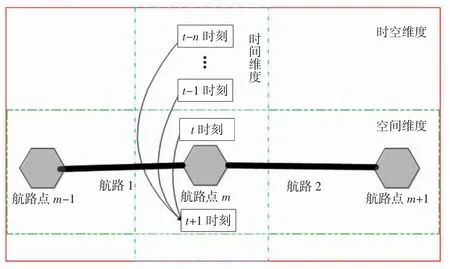
图2 K近邻预测模型Fig.2 K-nearest neighbor prediction model

根据K近邻算法思想，融合时间维度和空间维度的状态向量，预测结果相对于仅考虑时间维度的状态向量往往更精确，原因在于其能匹配到与实测数据更相似的近邻。如表1所示，为比较不同状态向量的差异，列出对应的物理意义。

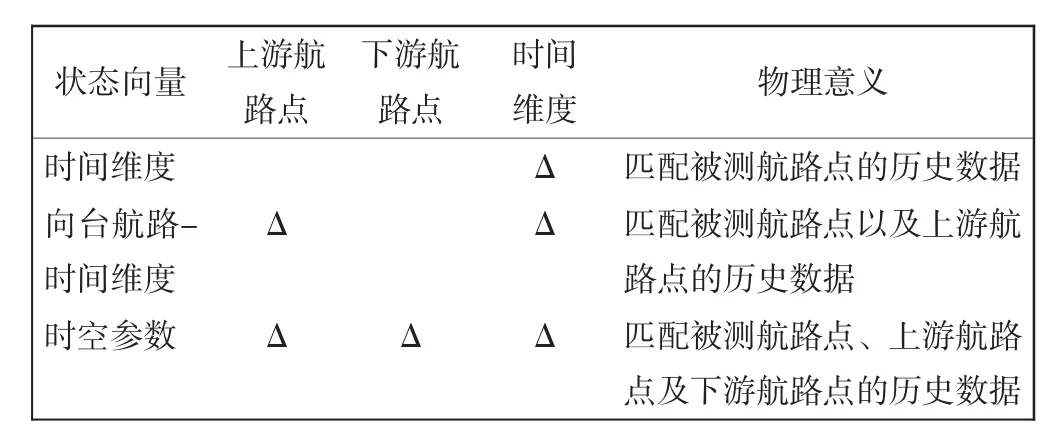
表1 3种状态向量Tab.1 Three state factors

2.2.1 时间维度

当模型只建立时间维度的状态向量时，预测t+1时段的m点的航班架次，仅参考了该航路点历史时段的航路架次。基于该模型的状态向量为（Pm（t）、Pm（t-1）、Pm′（t）、Pm′（t-1）），其中Pm′（t）、Pm′（t-1）分别为历史数据库中被预测航路点t时段和上一时段的航班架次。

2.2.2 向台航路-时间维度

在引入时间维度的基础上，此模型还加入了上游航路点（m-1点）向台飞行的航班架次。基于该预测模型的状态向量为（Pm（t）、Pm（t-1）、Pm-1（t）、Pm′（t）、Pm′（t-1）、P′m-1（t））。

2.2.3 时空参数模型

此模型同时考虑时间维度和空间维度的状态向量，较向台航路-时间维度模型，又综合考虑了下游航路点（m+1点）背台航路架次与m点的关系。基于该模型的状态向量为（Pm（t）、Pm（t-1）、Pm-1（t）、Pm+1（t）、Pm′（t）、Pm′（t-1）、P′m-1（t）、P′m+1（t））。

2.3 带权重的距离衡量方式

空中交通系统具有周期性和变异性，所以在不同历史时段下，交通环境各异导致同一航线的航班架次差异很大，在预测下一时段航路状态的主次程度也大相庭径。按照现有理论，利用带权重的方法改良传统的距离衡量方式，可能会搜索到与现阶段实测数据关联度越大、信息量越接近的近邻。故在引入时间维度来建立状态向量时，对各个子数据使用相关系数权重法以及指数权重法这两种距离衡量方式。

2.3.1 相关系数权重法

相关系数权重法基于统计学中相关系数，挖掘预测时段数据与历史数据不同时段的关联程度，从而确定该时段对于预测下一阶段航班状态的主次程度。如图3所示，ωn为t-n+1时段的历史数据与t+1时段数据的Spearman相关系数。

2.3.2 指数权重法

指数权重法是以预测时段与历史时段的时间距离来确定各个子数据的权重，时间距离由近到远依次为，如图4所示。

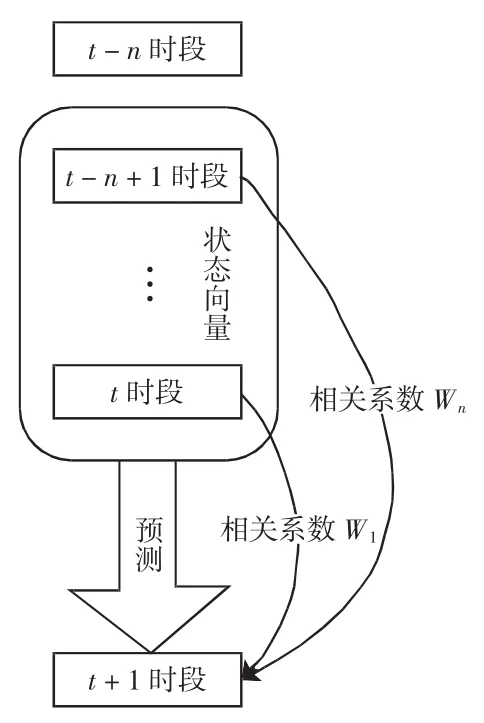
图3 相关系数模型Fig.3 Correlation coefficient model

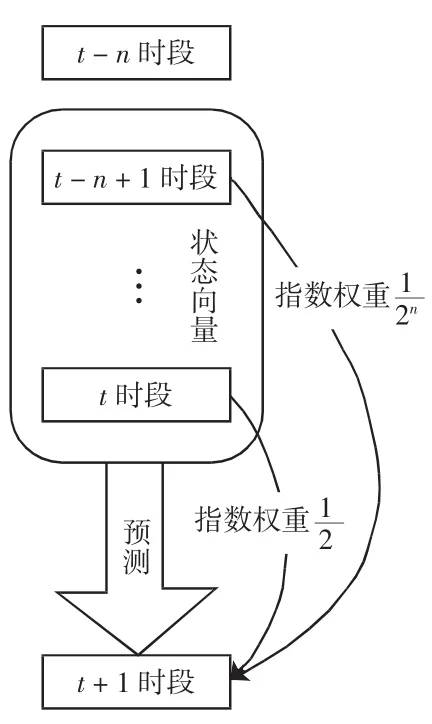
图4 指数权重模型Fig.4 Index weighting model

2.4 不同权重的预测算法

特征向量相似度越高，彼此间的距离就越小，在预测过程中，需选取适当方法将距离转化为权重。因此，针对近邻分配权重提出了两种方案：反函数法和高斯函数法。

2.4.1 反函数法

反函数法返回距离的倒数，执行速度快，易于实现，是一种表述距离越近权重值越大的简单方式，即

其中：di为现阶段数据与第i个近邻的距离。

2.4.2 高斯函数法

高斯函数法是返回距离对应的高斯函数值，避免了近邻项赋以很大的权重，而稍远的项权重“衰减”过快的一种赋权方式，即

其中：di为现阶段数据与第i个近邻的距离；c为一常数。

3 计算结果分析

3.1 数据获取与处理

数据来自某扇区雷达原始数据表，选用流量较大的航路航线，并划分成最小航段（不考虑方向）：A1-B、A2-B、B-C。如图5所示，由上往下依次是航路点A、A2、B、C。采用该扇区 500天 08：00～ 20：00雷达数据，统计飞行航迹信息，08：00～20：00共12个时段（每个时段均为60min）的统计数据，飞机实时航迹数据包括SSR、航班号、位置坐标、高度、航向等，共计6 416 800条航迹信息。

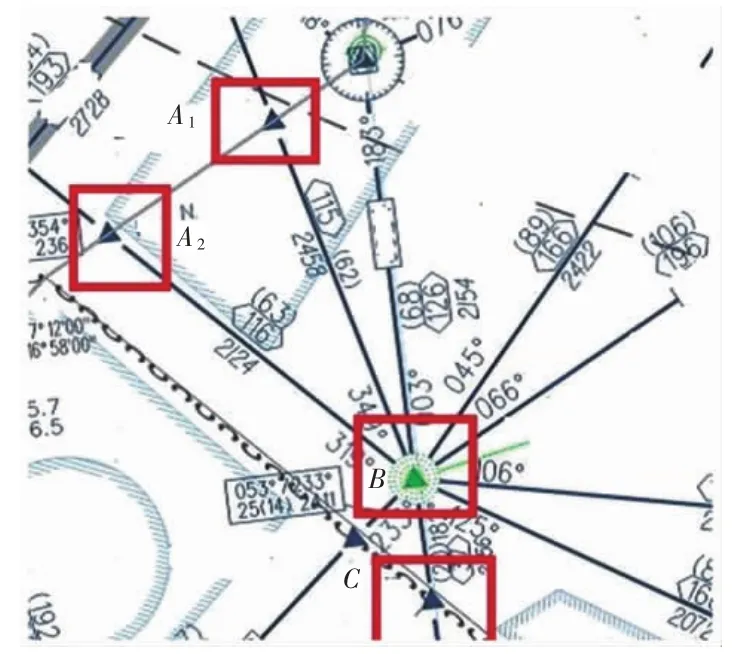
图5 航路图Fig.5 Routemap

对原始飞行航迹数据做如下处理：

1）以航路宽度10 km为范围，统计每个时段每个航路点10 km范围内所有飞机架次数；

2）依据 1）分别统计一日内 8：00～20：00其他时段过4个点的飞行架次数据，如表2所示。全部统计完成，得到500天全时刻过该航路点飞机流量架次数。

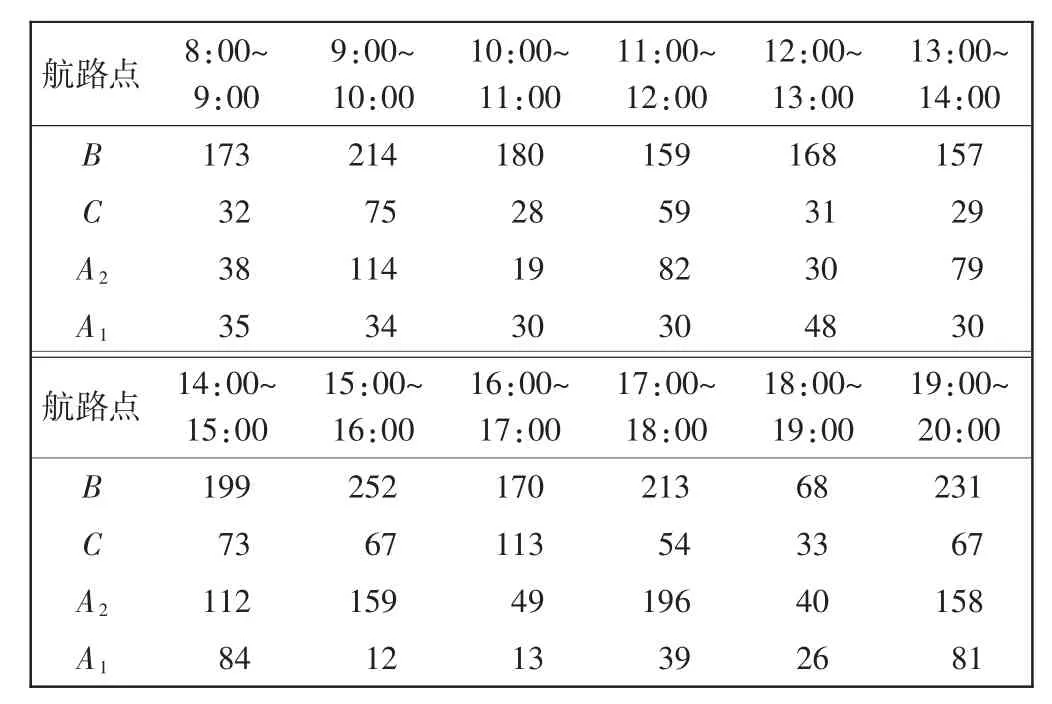
表2 4个航路点的流量Tab.2 Traffic flow in four way points

样本数据被随机划分为两类，一类为数据库样本，另一类为测试样本，其中有100天的数据集是测试样本，利用交叉验证法对误差进行评估。

3.2 K值的选取

K的选取对于K近邻模型有着重要意义，过小或过大的K值都会导致预测精度的减小。本文取4～20进行比较，如图6所示。可以发现，随着K值的增大，预测误差不断减小，但下降幅度不大。考虑到模型对鲁棒性和泛化能力的要求，取K=6进行下一步研究。

图6 K值的选取Fig.6 Selection of K value

3.3 不同状态向量的比较

运用无权重的K近邻模型对不同状态向量的精度进行检测，4个航路点下一时段飞机流量的预测效果可通过测试样本进行分析，结果如图7所示。取K=6时反函数法在相关系数权重下计算所得数据。

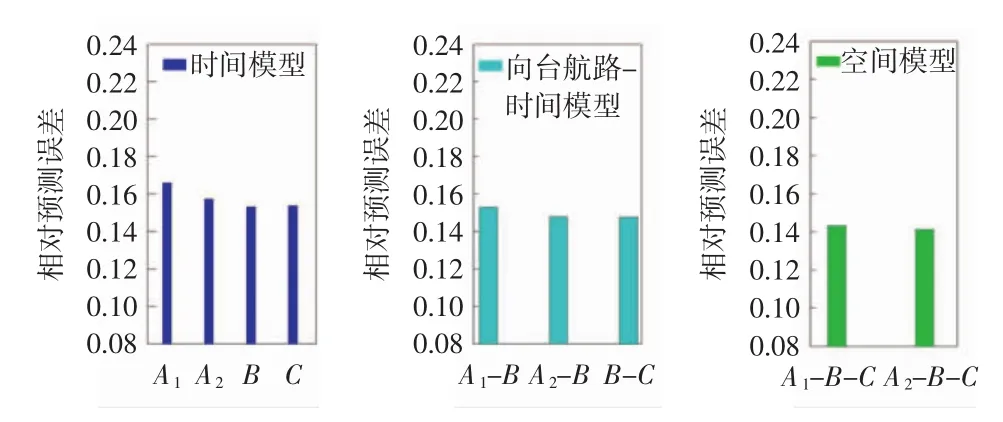
图7 不同状态向量的比较Fig.7 Comparison of different state vectors

第1种模型表明单纯采用时间维度的状态向量的K近邻方案，平均相对预测误差为15.7%，其预测效果显然不如采用时间维度和空间维度的状态向量的预测方案。第2种模型引入了向台航图数据，平均相对预测误差为14.9%，预测精度相比于第1种预测模型精度得到了提升。第3种模型取B台作比较，同时考虑时间维度和空间维度的状态向量，平均相对预测误差为14.2%，较上游航路点-时间维度模型，其又综合考虑了下游航路点流量与B台的关系，预测精度较模型2又得到了提升。模型汇总如表3所示。

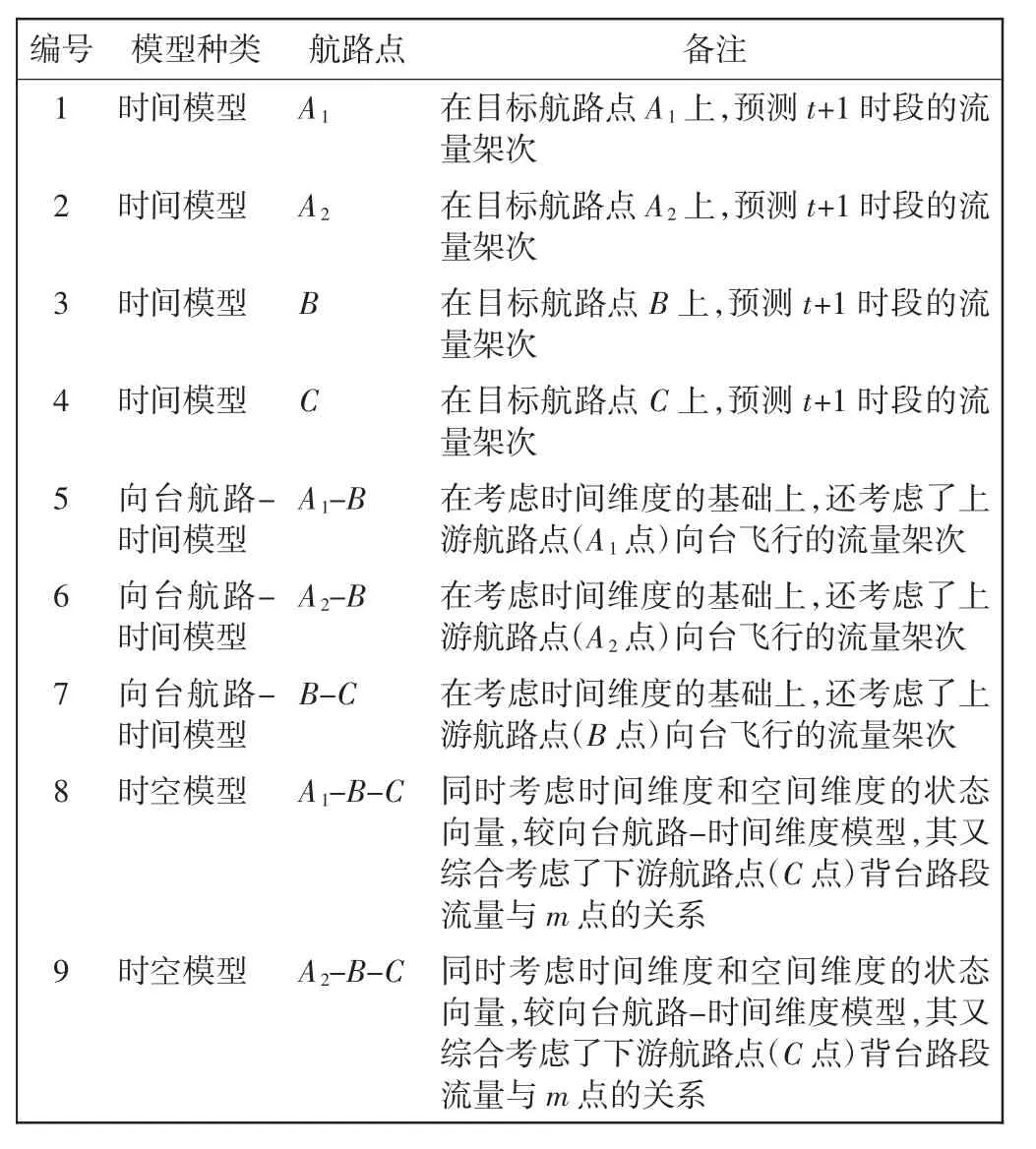
表3 模型汇总与说明Tab.3 Summary and explanation ofmodels

3.4 不同距离权重之间的比较

基于数据库样本和测试样本数据，运用相关权重和指数权重法检验带权重的距离衡量方式对模型的改进效果，结果如图8所示。取K=6时反函数法在时间维度下的4组数据，比较在4个航路点上分别用不带权重法、相关系数权重法、指数权重法进行数据演算的效果。其中不带权重法的预测效果最差，平均相对预测误差为15.79%，相关系数权重法的预测效果较好，平均相对预测误差为15.73%，而指数权重法的预测效果最好，平均相对预测误差为15.60%。这说明采用指数权重法和相关系数法对K近邻模型进行预测是可行的，并能提高预测精度。

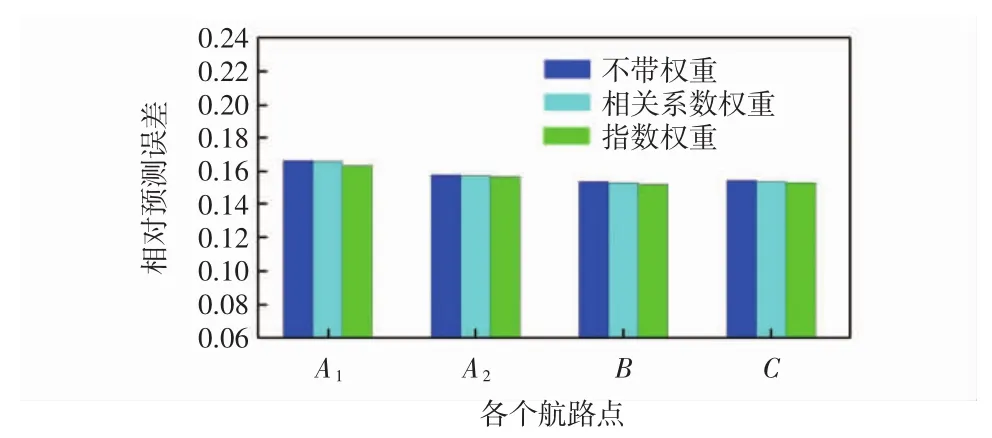
图8 不同距离权重Fig.8 Comparison of different distance weighting

3.5 不同预测算法的比较

比较反函数和高斯函数下的不同预测权重，取K=6时无权重下两种预测算法的数据进行比较。其中，无权重距离下的高斯函数法预测的时间维度模型、向台航路-时间模型、时空参数模型的误差分别为15.27%、15.26%、15.21%，而无权重距离下反函数法预测的时间维度模型、向台航路-时间模型、时空参数模型的误差分别为15.79%、14.92%、14.20%。从图9可以看出，高斯函数预测权重法在时间维度模型下优于反函数法，在引入空间参数后总体逊于反函数法。

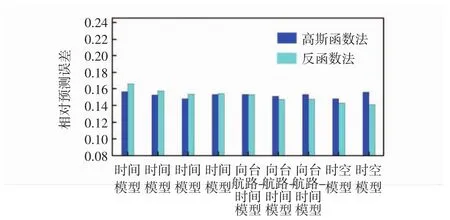
图9 不同预测算法的比较Fig.9 Com parison of different prediction algorithm s

4 结语

基于原有的K近邻算法预测短期交通流并进行优化：引入空间维度，建立了时空参数的状态向量，相对以往单纯的时间维度，不仅提供了考察航路流量的新角度，还有效地增加了预测精度；在原有无权重欧拉距离的基础上，合理分析历史数据间的特点，加入了相关系数权重和指数权重；尝试性地引入高斯函数来确定预测算法权重。选取某扇区4个航路点为研究对象，利用雷达数据对模型进行检验。虽然在某些样本数据下运用高斯函数确定预测权重得到了不错的效果，但由于高斯函数的参数取一常数，无法根据样本数据特性进行变化，今后通过改进算法实现自动调参能够进一步加强其实用性和预测精度。

[1]刘永欣,赵德斌.基于管制员知识的终端区飞行冲突解决模型[J].中国民航大学学报,2016,34(3):6-8,16.

[2]DAVISGA,NIHAN N.Nonparametric regression and short-term freeway traffic forecasting[J].Journal of Transportation Engineering,1991,117(2):178-188.

[3]SMITH B L,DEMETSKYM J.Traffic flow forecasting:comparison of modeling approaches[J].American Society of Civil Engineers,1997,123(4):261-266.

[4]翁剑成,荣 健,任福田,等.基于非参数回归的快速路行程速度短期预测算法[J]．公路交通科技,2007,24(3):93-97:106．

[5]于 滨,邬珊华,王明华,等.K近邻短时交通流预测模型[J].交通运输工程学报,2012,12(2):105-111.

[6]谢海红,戴许昊,齐 远.短时交通流预测的改进K近邻算法[J].交通运输工程学报,2014,14(3):87-94.

[7]张 涛,陈 先,谢美萍,等.基于K近邻非参数回归的短时交通流预测方法[J].系统工程理论与实践,2010,30(2):376-384.

[8]熊亚军,廖晓农,李梓铭,等.KNN数据挖掘算法在北京地区霾等级预报中的应用[J].气象,2015,41(1):98-104.

Short-term air traffic flow forecast based on K-nearest neighbor algorithm

ZHAO Yuandia,CHEN Junfua,LIU Zeyua,SHENG Shouqiongb,BAIZhijiana
（a.College of Air Traffic Management； b.College of Science,CAUC,Tianjin 300300,China）

It’s worth to predict available short-term air traffic flow and reduce ATCO workload.An air traffic flow model is built based on K-nearest neighbor.First,relative errors from different K values are compared to determine the appropriate K values.After that,space parameter is introduced to improve the model.Then these three kinds of state vectors are combined and new K-nearest neighbor models are proposed including time dimension model,to route-time dimension model and time-space parameter model.Radar data within a certain sector is used to test K-neighbor model,showing out that K-nearest neighbor model with time-space parameter has minimum error,whose average error equals to 14.6%.Distance measuring method based on weight index can attain the goal of prediction accuracy optimization.Gaussian function can produce a better result under time parameter model while it is weaker when space parameter is taken into consideration.Statistics show prediction’s error is only 13.94%under the index weight distance method of inverse function model with time-space parameter.The improved K-nearest neighbor model has applicability for different traffic situations and strong portability for complicated air traffic situation of China.

short-term air traffic flow prediction;K-nearest neighbor model;state vector;space parameter;Gaussian function

赵元棣（1983—），男，天津人，助理研究员，博士，研究方向为空管数据挖掘与处理.

U8

A

1674－5590（2017）05－0001－05

2016-12-08；

2017-03-07

国家自然科学基金项目（U1533106）

?

刘佩佩）