基于BP 方程算法的多机型机组恢复时空网络模型
张 青 ,马永秀 ,杨正全 ,陈增强 ,2
(1.中国民航大学理学院,天津 300300;2.南开大学计算机与控制工程学院,天津 300350)
基于BP 方程算法的多机型机组恢复时空网络模型
张 青1,马永秀1,杨正全1,陈增强1,2
(1.中国民航大学理学院,天津 300300;2.南开大学计算机与控制工程学院,天津 300350)
航空公司工作中的一个重要部分就是不正常机组排班恢复,为减少机组排班不正常对航班运行计划的影响,以航空公司资源浪费最小为优化目标,在分析不正常机组排班要满足的客观约束条件下,建立了多机型不正常机组排班恢复的时空网络数学模型,并针对国内某航空公司的实际运营数据运用该模型进行实例分析,利用最小顶点覆盖(MDS)和BP方程法求解。结果表明:用MDS和BP方程法不仅加速了机组排班恢复的时间,更增加了机组排班恢复的鲁棒性。该方法利用完全相关结构,当遇到某些突发情况时,机组排班能自动随之调整,操作起来方法简便,适用面广,并且系统性强,便于普及和推广。
BP方程;最小顶点覆盖;机组排班恢复;能量函数;时空网络模型
?
民航运输作为现代运输业之一,在国民经济中占有重要地位。长期以来,不正常机组排班恢复是航空公司运行控制的重要内容之一,是航空公司的主要研究课题。合理的机组排班恢复不仅避免了航班的再次延误,还能够提高机队的利用效率,有效地降低运营和闲置成本。机组排班恢复问题的优化目标主要包括成本最小、航班尽早恢复等,约束条件要满足航班覆盖,每个飞行出勤不超过8 h,等待衔接时间在允许的上、下限之间,第2天第1个航班的起飞机场与前一天晚上最后一个航班的目的地相同等要求。
针对不正常机组恢复,主要有两个研究方向:事后研究和事前研究,而我们主要针对后者。事前研究是指在机组排班计划编制阶段,设计机组排班计划的鲁棒性,提高机组排班计划的抗干扰能力。虽然研究机组排班问题的文献很多,但不正常机组排班恢复问题的研究却非常少。Ellis L Johnson[1]讨论了单个机组延误无法正常连接后续航班任务的问题,给出了单机组恢复问题的数学模型和解决方案;Wei等[2]建立了机组恢复的多商品整数网络模型,设计了基于分枝定界的启发示算法;Stojkovic等[3]研究了以成本最小为目标函数,在给定航班计划下恢复机组任务串的问题,将列生成算法植入分枝定界搜索树进行求解;Lettovsky等[4]提出了一种最小化机组恢复成本的方法,通过定义恢复时间和受扰机组的最大数量,用列生成算法选择最小的机组任务串集合;Medard等[5]从机组成员角度恢复机组,先构建一个整数规划模型,求解机组配对,然后基于任务期的网络上求K最短路问题;Rudiger Nissen和KnutHaase[6]针对欧洲航空公司的需要提出了一个基于执勤期的机组恢复模型,采用分枝定价法和列生成法求解问题;北美洲和欧洲的机组薪酬制度不同。GUOYufeng等[7]针对地域的薪酬制度和航空公司的运作特点,对机组恢复问题进行了研究。其中,某些机组排班恢复的研究已取得了很好的成果,然而这些理论研究成果在实际应用中却没能发挥预期的作用,并且操作起来也比较困难,这是由于航空运输系统是个复杂的系统,不正常机组排班涉及的各种资源之间是相互依赖和影响的。
目前对不正常机组恢复的研究,利用约束规划方法,思路清晰,模型表达简洁,一直是学术界研究的重点,也取得了很多成果。但其规划方法比较固定单一,面对复杂的机组排班问题运行时间非常长,而且很难找到有效的求解方法,本文对不正常机组排班进行了研究,运用顶点覆盖方法给出了机组可执行的航班串,然后采用BP方程,将非线性的NP难多项式问题转化成线性多项式求解问题。不仅降低了运算的复杂度,而且首次将物理方法运用到了求解数学模型上,成功解决了非线性式子编程复杂的缺点,并且为机组排班的进一步完善创建了很大的研究空间。
1 问题描述
航空公司不正常航班恢复通常包括以下4个问题:
1)对受扰航班时刻表通过延误或取消航班来修复;
2)通过飞机交换、机型替换、调机等进行飞机恢复;
3)为受扰旅客重新安排其行程进行旅客恢复;
4)采用机组交换、加机组、备份机组等策略进行机组恢复。
前3个问题目前都有很多学者对其进行研究并取得一定的成果,并不纳入本研究范围。本文研究了一个飞行日内不正常多机型机组恢复问题。多机型机组的恢复问题是一个从局部优化达到全局优化的问题,可被视为一个最小顶点覆盖问题。但需动态地考虑其时空链接和空间衔接,并且不正常机组任务恢复最大的特点在于加机组策略的使用。即指一旦航班到位但没有后续机组执行时将机组像乘客一样搭乘航班,去某机场执行后续的航班任务。但无论是加机组航班还是机组实际执行的航班,其航班衔接方式如图1所示。故根据机组特点,设计以最小顶点覆盖的方法利用信息传递来求解出最优解。同时,为提高机组的工作效率,航空公司希望其有效飞行时间占总工作时间的比例越高越好,因此,模型中有关不正常机组恢复的部分不仅要考虑时间合法性的约束,并且为了降低成本还要尽量减少加机组、备用机组等策略的使用。

图1 航班衔接方式Fig.1 Flight connection mode
2 时空网络数学模型
本文在构造时空网络图中,用节点表示飞机可能停留的机场。用连接两个节点的边表示航班,每条边的出发点都表示在该点有可利用的机组。因此,有的航班边在网络图中会用推迟后的边表示,产生使用加机组或使用备用机组成本。从而将不正常机组恢复成本问题利用时空网络图[8-9]转换成数学模型。这样便将不正常机组恢复问题转换成了求解成本流最小问题。
2.1 符号定义
以下是对数学模型中使用到的上下标、集合、参数、变量的解释:
上下标指示 z为正常机组指示;j为加机组指示;b为备份机组指示;s为机组基地指示;k为机型下标指示;r为配对下标变量指示;i为航班下标变量指示。
集合 F为航班集合;P为可行配对集合;S为机组基地集合;Z为正常机组集合;J为加机组集合;B为备份机组集合。
2.2 模型建立
数学模型为
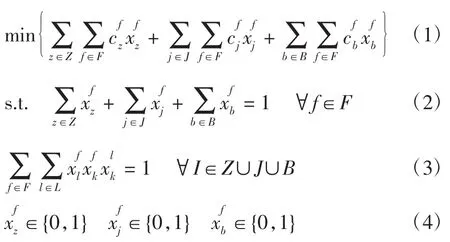
模型中式(1)为目标函数,其表示使航空公司资源浪费最小,分别包括机组闲置成本、加机组成本和备用机组成本;式(2)为航班覆盖的约束,即保证在一个航班上机组,加机组和备用机组至少有一个;式(3)为机组执照约束,即对机组要执行的航班,必须持有该航班对应飞机机型的执照;式(4)为0,1整数约束。
3 模型算法
3.1 最小顶点覆盖问题
顶点覆盖问题用于工程应用领域许多实际的资源最优配置问题,也是计算复杂性理论研究领域最基本的NP完备问题之一。Hartmann和Weigt[10]在专著中全面和详尽地探讨了顶点覆盖问题的统计物理理论和算法。
考虑一个网络 G,其由 N 个节点(i=1,2,…,N)和这些结点之间的M条边构成,每一条边连接两个不同的节点。网络G的覆盖是由G中的一部分节点所构成的一个集合,其具有这样的性质,即G中每一条边的两个端点至少有一个端点是其元素。可将网络G想象为一个大型博物馆,网络G的每条边对应于该博物馆的一条走廊,网络G的每个节点对应于这些走廊的终点以及两条或多条走廊的交汇点。在博物馆的一些走廊终点和走廊交汇点设置了安保岗,有保安在岗上监视展品的安全,防止意外情况发生。为不留死角,每一条走廊必定有一头设置了安保岗。每一种满足这一约束的安保岗设置方式,显然就对应于网络G的一个覆盖。网络G的平庸覆盖包含所有N个节点。显然平庸覆盖有冗余存在,是不经济的。例如:一个小网络(包含N=6个节点和M=9条边)的3种不同覆盖方式,其能量分别为6(平庸覆盖)、4和3(最小覆盖)。该网络只有1个最小覆盖。
为了和自旋玻璃[11-12]联系起来,定义N节点构型:c={c1,c2,…,cN},其中,ci∈{0,1}是定义在节点 i上的微观状态,ci=1表示节点i包含于覆盖集合,ci=0则表示i不属于覆盖集合。从而构型C需满足的约束条件为
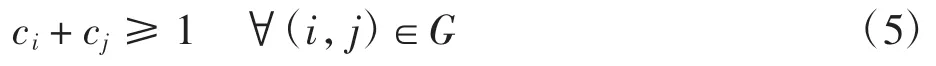
其中,ci∈{0,1}对于一条边(i,j)成立,就称为该边被覆盖,反之就称该边未被覆盖。那么进一步定义构型C的能量为

该能量就是C所对应的覆盖集合中的节点数目。把满足上述约束条件且能量为全局最小的构型C称为网络G的最小覆盖。如图2所示,网络G的最小覆盖一定存在,但不一定是唯一的。

对于任意给定的网络G,寻找顶点最小覆盖的算法步骤为:
1)初始化子网络g=G,即g包含原网络的所有节点和边。初始化集合L,使其包含网络g中所有连通度为1的节点。
2)如果集合L为空,则停止;反之,从L中挑选一个节点j,并覆盖j在子网络g中的最近邻节点i。
3)将节点i在子网络g的所有边都从g中删去;更新集合L,使之包含化简后的子网络g中所有连通度为1的节点。
4)重复步骤 1)~2)直至程序停止。
也就是说,找出目前网络中一个连通度为1的节点并将连到其最近邻节点上的边都从网络上除去,直到网络中不再存在连通度为1的节点。
对于找到的不止一个的最小顶点覆盖,通过分析其实现概率来进行选择。考虑一个N→∞且平均连通度为常数C的随机网络G。那么随便挑选一个网络中节点i,则i的连通度ki=k的概率服从泊松分布,即,故可分以下几种情况:
1)i的连通度ki=0,因而i无需被覆盖,这种情况对应的概率为e-c。
2)i的连通度ki=1,假设其邻近节点为j。
a)如果边(i,j)可以在保留 i的情况下除去,那么节点i等价于没有任何最近邻节点,其无需被覆盖。这种情况对应的概率为c e-cρ0,其中ρ0是网络G的一条边在其一个端点被保留情况下的概率。
b)如果 j的除边(i,j)以外的其它边都可以在保留i的情况下除去,j等价于连通度为1的节点,那么覆盖节点j和节点i在能量上是等效的。
c)如果节点j不属于上述两种情况,那么覆盖j是比覆盖i更经济的方案,节点i无需被覆盖,这种情况对应的概率为c e-c(1-ρ0-ρ1)。
3)i的连通度 ki≥ 2。
a)如果i所连的所有边都可以在保留i的情况下被除去,那么i等价于没有任何最近邻节点,其无需被覆盖,这种情况对应的概率为
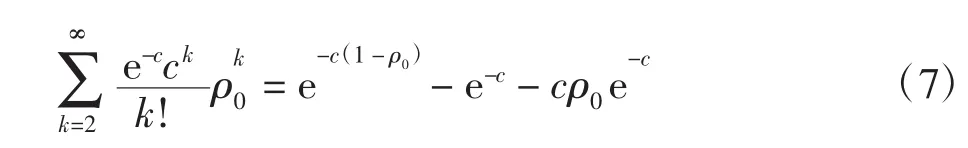
b)如果i的ki条边中,有ki-1条可以在保留i的情况下除去,而剩下的节点可设为j,那么i和j都等价于连通度为1的节点,边(i,j)对系统基态能量的贡献为1,这种情况对应的概率为

c)如果i的ki条边中,有ki-1条可以在保留i的情况下除去,而剩下的节点可设为j,不能被除去,那么i无需被覆盖,这种情况对应的概率为
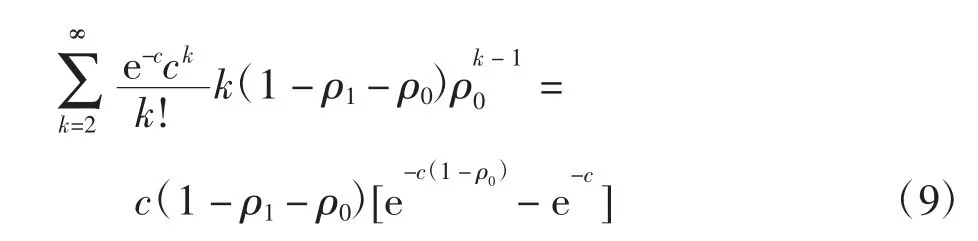
d)如果i的ki条边中,至少有2条可以在保留i的情况下除去,那么i可以被除去,且覆盖它是最经济的,这种情况对应的概率为

由上述分析可知,任意选取的节点i属于不可除去的概率为
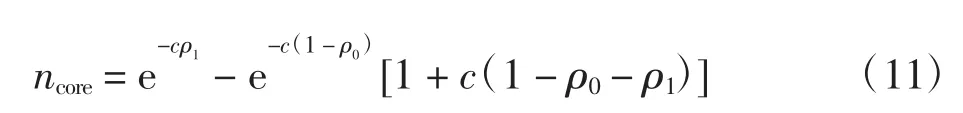
3.2 BP方程
BP(Bethe-Peierls)方程[13]在自旋玻璃统计物理和网络科学中有广泛的应用。要了解BP方程及其应用有以下几个内容。首先要知道能量函数[14-15]和因素网络,为方便起见,假定每个粒子(i=1,2,…,N)的微观状态是分立的且只有两个可能的态,用自旋σi=+1和σi=-1来表示。N个粒子自旋态的集合构成系统的一个微观构型{σ1,σ2,…,σN}。故能量函数为

并且常常用因素网络来直观地描述一个多变量系统中的统计关联[16-18]。其次是配分函数和基态构型。当系统达到平衡后,其宏观性质就不再随时间而改变,而系统微观构型σ的平衡概率分布为玻尔兹曼分布,即
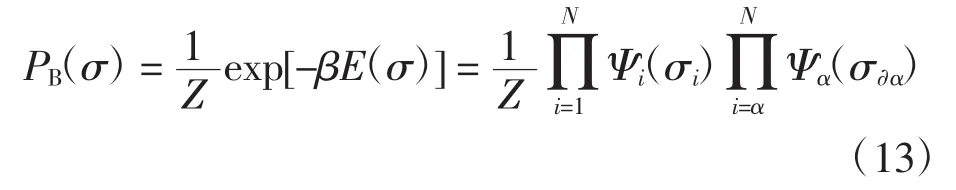
其中:β为逆温度,其与温度呈反比关系,β≡(kBT)-1;Ψi≥0是变量节点i感受到的外场所贡献的权重因子,而Ψα≥0是内部相互作用α所贡献的权重因子,其表达式分别为
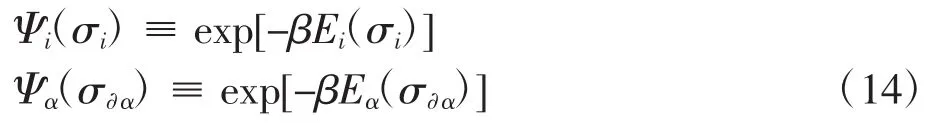
Z是玻尔兹曼分布的归一化系数,称为配分函数,即
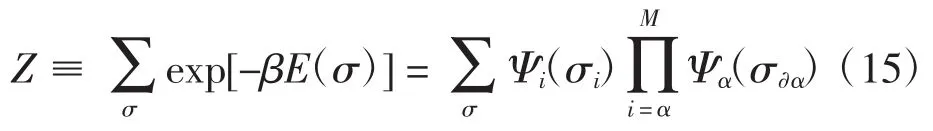
在温度T趋向于0时,一个达到平衡的宏观系统的平均能量将趋向于系统的基态能量,记为E0。基态能量是系统所有微观构型所对应的能量最小值,即

下面通过一个简单模型系统来介绍这一方程。随机规则网络中包含N个变量节点,每个变量节点i都有K个最近邻变量节点,因而其受到K个自旋耦合作用影响。该铁磁系统的一个自旋微观构型σ的能量为

其中:网络中所有边(i,j)上的自旋耦合常数都相同(=J)。
任意节点i的自旋边缘概率分布的定义式为微观构型能量E(σ)可分解成两部分

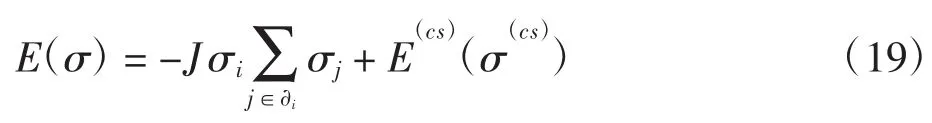
其中:∂i表示节点i的最近邻变量节点组成的集合,而σ(cs)表示i之外的所有其它N-1个变量节点的自旋构型,即 σ(cs)= σ/σi={σ1,…,σi-1,σi+1,…,σN}。能量E(cs)是将变量节点i从网络中删除后剩下的能量,其与节点i的自旋σ1无关,是所有其它N-1个变量节点自旋的函数,即
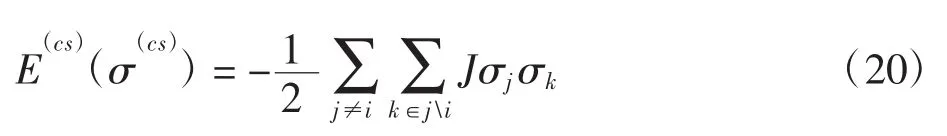
其中:∂ji表示变量节点j除节点i之外的所有其它最近邻变量节点组成的集合,从而有

其中,qi(σ)即为要求的BP方程核心,在随机网络系统中,如果系统的特征关联长度有限,那么BP近似对于这样的随机网络在系统热力学极限下就趋于精确。
3.3 基于BP方程求解多机型机组恢复问题
鉴于多机型机组恢复问题是NP难解的,那么在较短的时间内得到精确解仍会存在很大的困难,大多数学者都是基于优化不同的规划算法对此问题进行优化,存在的不足之处就是操作起来都很困难,不易实现,并且对航班的衔接也有要求,不能使多机型机组恢复问题简便快捷的实现。而且大多数优化算法大同小异,进步成效并不大。本文通过将机组看成节点,利用最小顶点覆盖的方法得到现执行机组与执行后续航班机组之间的连接关系。将机组恢复需满足的约束条件转化成能量函数,考虑每个选择的概率从而得出最优选择。将机组恢复转化的因子如图3所示。

图3 顶点覆盖因子图Fig.3 Vertex cover factor diagram
故所求概率函数为

4 实例计算及结果分析
航空公司中不正常多机型机组排班恢复是在飞机路线恢复完成之后进行的,本文采用MatlabR2014a优化软件进行求解。给出案例如表1所示。
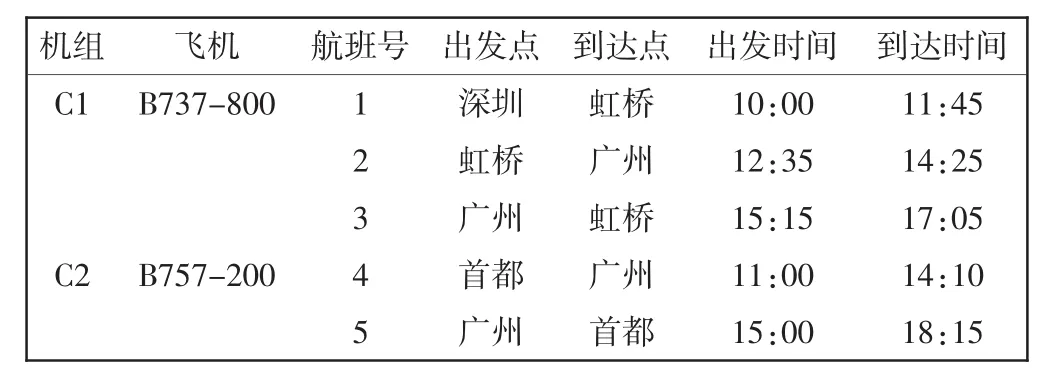
表1 机组排班表Tab.1 Crew schedule
本文在计算时基于以下假设:①机组闲置成本按照航班取消或航班推迟后机组闲置总时间乘以每分钟的闲置成本,这里每分钟闲置成本按120元计算。②机组换机型飞行时,若用大飞机换小飞机,由于飞机比原来容量大,因此产生换机成本,并将该成本加到加机组成本中合并计算;反之,用小飞机换大飞机则不产生换机成本。例如,若B737-800代替B757-200,那么飞机容量变大则要产生还击成本,这里规定加机组成本为1 000元。③若使用备用机组,则按照每次10 000元计算,这个取值基于换机型时产生的设备及人工成本,以及对于机组成员的工资补偿。
根据算例得到的因子如图4所示。
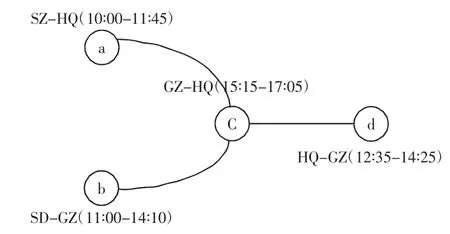
图4 机组恢复因子图Fig.4 Crew recovery factor graph
那么,可求得配分函数Z和相应的概率函数为
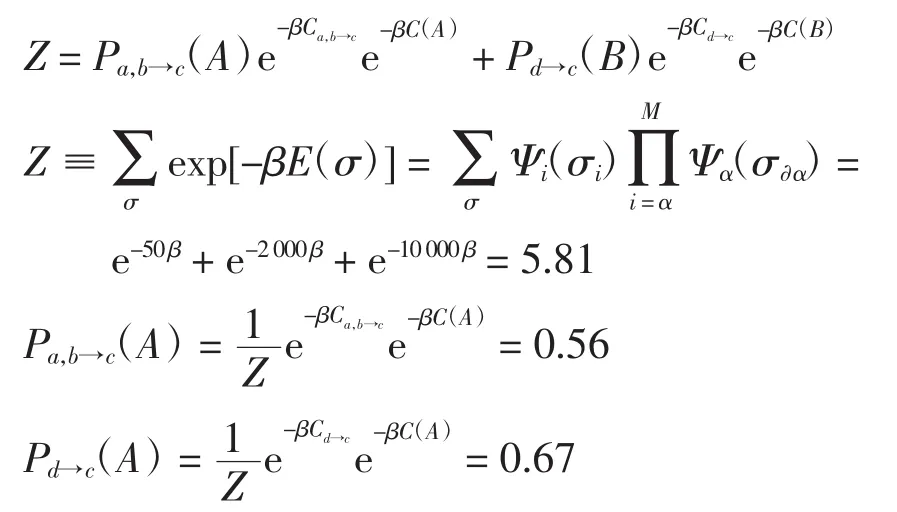
所以最终花费为人民币168 676元。
5 结语
本文针对发生突发事件不正常机组排班恢复的情况,根据算例数据,建立了多机型时空网络数学模型,通过最小顶点覆盖方法,利用BP方程求解,并用MatlabR2014a优化软件进行运算。实验结果表明,通过优化多机型时空网络模型得出的成本较由于机组不到位航班再次取消的成本大幅度降低,并且维护了航空公司的信誉度,获得了更多隐性利益。但本文尚存在一些不足之处,模型只考虑了一少部分机组恢复约束条件,把松弛时间均设为合理的,并没有考虑到对于大型机场的使用,这些均为进一步的研究方向。
[1]ELLIS L JOHNSON.Final Report to North Airlines on the Crew Recovery Problem[D].The Lugistic Institute,Georgia Institute of Technology,1994.
[2]WEI G,YUG,SONG M.Optimization model and algorithm for crew management during airline irregular operations[J].Journal of Combinatorial Optimization,1997,1(3):305-321.
[3]STOJKOVICM,SOUMISF,DESROSIERSJ.The operational airline crew scheduling problem[J].Transportation Science,1998,32(3):232-245.
[4]LETTOVSKY L,JOHNSON E L,NEMHAUSER G L.Airline crew recovery[J].Transportation Science,2000,34(4):337-348.
[5]MEDARDCP,SAWHNEYN.Airlinecrew scheduling from planning to operations[J].European Journal of Operational Research,2007,183(3):1013-1027.
[6]NISSEN R,HAASE K.Duty-period-based network model for crew reseheduling in European airlines[J].Journalof Scheduling,2006,9(3):255-278.
[7]GUO Yufeng,SUHL L,THIELM P.Solving the airline crew recovery problem by a genetic algorithm with local improvement[J].Operational Research,2005,5(2):241.
[8]MESQUITAM,PAIASA.Set partitioning/covering-based approaches for the integrated vehicle and crew scheduling problem[J].Computers&Operations Research,2008,35(5):1562-1575.
[9]LETTOVSKY L,JOHNSON E L,NEMHAUSER G L.Airline crew recovery[J].Transportation Science,2000,34(4):337-348.
[10]HARTMANN A K,WEIGT M.Phase Transitions in Combinatorial Optimization Problems:Basics,Algorithms and Statistical Mechanics[M].Hobken,New Jersey:John Wiley&Sons,2006.
[11]GARDNERE.Spin glasseswith p-spin interactions[J].Nuclear Physics B,1985,257:747-765.
[12]KIRKPATRICK T R,THIRUMALAID.p-spin-interaction spin-glass models:connections with the structural glass problem[J].Physical Review B,1987,36(10):5388.
[13]李腊梅,吴汉松,王树人.基于BP算法的模糊关系方程解法及仿真[J].计算机仿真,2007,24(4):149-151.
[14]王春妮,王 亚,马 军.基于亥姆霍兹定理计算动力学系统的哈密顿能量函数[J].物理学报,2016,65(24):240501-240501.
[15]周雪梅,李 辉,潘 多.基于能量函数的故障诊断方法与实验[J].计算机工程与设计,2015,36(5):1385-1389.
[16]FREY B J.Graphical Models for Machine Learning and Digital Communication[M].Cambridge,Mass:MIT press,1998.
[17]KSCHISCHANG FR,FREY B J,LOELIGER H A.Factor graphs and the sum-product algorithm[J].IEEE Transactions on information theory,2001,47(2):498-519.
[18]许 锋,潘 琦,王一岚,等.工业过程多变量系统常规控制结构的频域设计[J].清华大学学报(自然科学版),2016,56(4):448-452.
Crew recovery time-space network model with various types of airplanes based on BP equation algorithm
ZHANG Qing1,MA Yongxiu1,YANG Zhengquan1,CHEN Zengqiang1,2
(1.College of Science,CAUC,Tianjin 300300,China;2.College of Computer and Control Engineering,Nankai University,Tianjin 300350,China)
Aircrew scheduling recovery is an important part of airlines work.To abate the effect on flight operation planning from abnormal aircrew scheduling,various types of airplane crew recovery time-space network model is built up.Before the establishment,the objective constraint according to abnormal aircrew scheduling is analyzed.Meanwhile,the minimum of airlines operation aircrew recovery of multi-types of airplanes based on time-space network model and heuristic binary search algorithm on costs is the optimization goal.These models are applied to the actual operational data of some domestic airline to carry on the instance analysis.Minimum vertex cover and BP(Bethe-Peierls) equation algorithm are used to solve it.Results showed that the usage of minimum vertex cover and BP equation algorithm accelerate the aircrew scheduling recovery and increase the robustness of aircrew scheduling recovery.They adjust automatically when some factor changes.Whole-related structure is employed to help aircrew scheduling automatically adjust to urgent change of factors.This model is simple to operate and with strong systematicness to be used widely.
BP equation algorithm;minimum vertex cover;aircrew scheduling recovery;energy function;time-space network model
张青(1965—),女,天津人,教授,硕士,研究方向为复杂系统建模与优化、多智能体系统等.
TP272
A
1674-5590(2017)05-0030-06
2017-01-10;
2017-02-22
国家自然科学基金项目(6157399);天津市自然科学基金项目(14JCYBJC18700);中央高校基本科研业务费专项(3122015C025)
?
杨媛媛)

