视觉SLAM 中三维点云配准的Cayley 方法
张鸿燕,王婧妍,周璐莎,王炳辉
(中国民航大学中欧航空工程师学院,天津 300300)
视觉SLAM 中三维点云配准的Cayley 方法
张鸿燕,王婧妍,周璐莎,王炳辉
(中国民航大学中欧航空工程师学院,天津 300300)
利用三维点对应关系估计摄像机的位姿矩阵是同步定位与地图构建(SLAM)系统的一个基本问题。由于系统的误差累积会导致点云尺度的漂移,三维点对应关系在误差干扰下从欧式变换退化为相似变换,在计算过程中需考虑尺度因子。利用Cayley变换来估计三维对应点之间相似变换的闭式算法,可方便地确定定位与构图过程中摄像机的位姿变化。仿真实验和误差分析验证了基于Cayley变换的配准算法的准确性与鲁棒性。该算法不仅可用于SLAM系统,还适用于计算机视觉中的三维重建与三维拼接问题。
同步定位与地图构建;点云配准;相似变换;Cayley变换
由三维对应点估计刚体的三维运动[1-3],即刚体运动估计问题,被广泛应用在姿态估计、图像配准、目标运动识别、机器人学等领域。该问题的本质就是估计运动过程中的姿态变换矩阵[4]
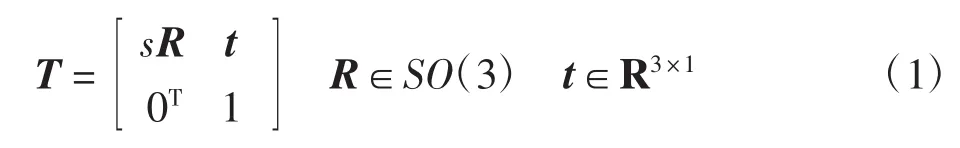
其中:R为旋转矩阵;SO(3)为三维旋转群;t为平移向量;s为尺度因子。一般地,s为正数,T矩阵是摄像机姿态变换(相似变换)矩阵;特殊地,s=1时,T矩阵是刚体运动变换(欧式变换)矩阵。在视觉同步定位与地图构建(SLAM,simultaneous localisation and mapping)系统中,摄像机运动姿态(R与t)实时估计是关键环节[5-6]。当视觉系统获得不同局部坐标系下的三维点云,即可估计摄像机的姿态变换矩阵,进而将点云配准到全局坐标系下。若系统所得点云无先验对应关系,通常选用迭代最近点(ICP)[1,7]算法进行配准,该算法计算复杂度高,用于实时处理时需硬件加速。对于无需硬件加速的SLAM系统,如ORB-SLAM[8],一般根据稀疏点云之间的对应关系估计三维点云配准矩阵。
针对三维对应点的配准矩阵计算,经典的估计算法包括Arun[9]提出的奇异值分解法、Horn[10]提出的正交分解法和单位四元数法[11]以及Walker[12]提出的对偶四元数法。Eggert等[13]分析了这4种算法的准确性、稳定性及效率,同时指出,无论从鲁棒性、效率还是收敛性考虑,闭式解(解析解)都优于迭代解。运动状态估计问题必然会涉及到旋转矩阵的计算。这些经典算法均采用Euler角、四元数或Rodrigues公式来表达三阶旋转矩阵。当数据误差较大时,得到的姿态可能是一个正交矩阵而非旋转矩阵。吴福朝[14]提出将Cayley变换应用于欧式变换估计,揭示了Cayley变换在摄像机姿态估计中的优越性。Cayley变换及旋转矩阵的Cayley表达是数学家Cayley[15]于1846年提出的,但在计算机视觉领域一直未引起足够的注意。Cayley方法的优点在于直接提供了一个旋转矩阵,无须校正与近似,而且只需3个对应点就能提供线性解[16]。
对于多数单目SLAM系统,由于缺乏绝对尺度信息,系统运行的累积误差会导致点云尺度发生漂移[8],从而使得对应点无法正常匹配。此时,三维点对应关系在误差干扰下已不是欧式变换而是相似变换。针对尺度漂移问题,ORB-SLAM系统采用Horn[11]提出的基于单位四元数的闭式算法,用四元数表达旋转矩阵,转化过程复杂,且在数据误差较大的情况下给出的可能不是旋转矩阵。针对三维对应点的相似变换问题,提出基于Cayley变换的闭式配准算法,避免了复杂的迭代过程,并直接给出旋转矩阵,使得不同局部坐标系下的点云配准在统一的坐标系与尺度之下。
1 点云配准与旋转矩阵的Cayley表达
已知SLAM系统在相邻k-1和k时刻构建的一组三维对应点为,点云配准算法根据点对应关系来计算两帧图像Ik-1和Ik所确定的摄像机姿态变换矩阵[4,17]
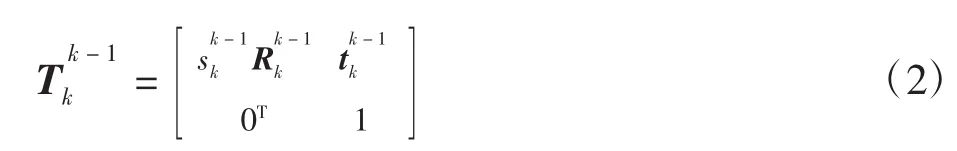

然而实际系统运行时存在累积误差,这会导致点云的相对尺度发生漂移,此时尺度因子,点对应关系转化为[18]
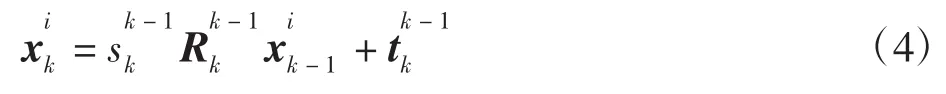


图1 三维点云坐标配准Fig.1 3D points registration
求解摄像机的位姿变换矩阵时,采用Cayley表达来表示旋转矩阵。Cayley变换是反对称矩阵与旋转矩阵之间的一对一映射。给定反对称矩阵W,则存在一个唯一的三维向量 w=[w1,w2,w3]T满足

旋转矩阵可由三维向量w表示成[15-16]
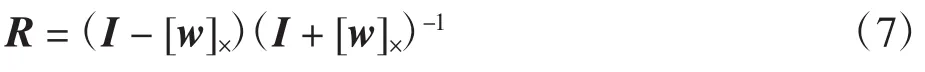
其中:向量w称为旋转矩阵R的Cayley表达。
由于本文只考虑相邻两帧图像确定的摄像机姿态变换矩阵,也就是计算一组三维对应点的坐标配准矩阵,为简化符号描述,省去上下标k-1和k,并记
2 点云配准的Cayley方法
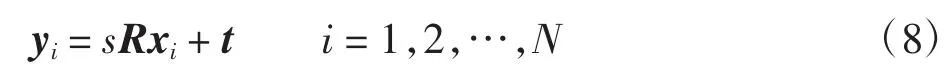
其中:s为尺度因子;t为平移向量;R为旋转矩阵。由于实际系统存在噪声,式(8)并不成立,而变成一个超定方程组。假设误差为
位姿变换参数(R,t,s)的估计问题转化为误差函数最小化问题

为得到较好的三维点云配准估计算法,先对原始三维点云数据进行0均值化,以简化误差函数的描述。
2.1 数据的0均值化

然后将点集中的各个元素减去质心坐标,得到各个点与质心之间的偏移距离,形成新的点云集合和,其中
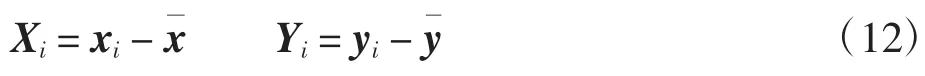
新生成的对应点之间的几何约束关系为

2.2 误差函数的等价描述
对于新的对应点集,其误差表示为
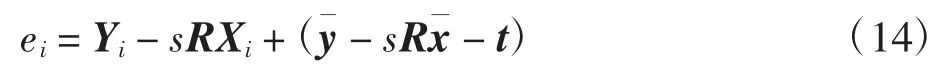
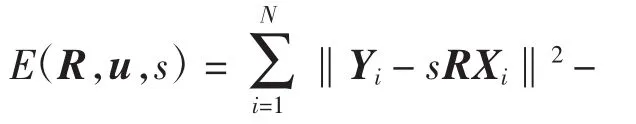
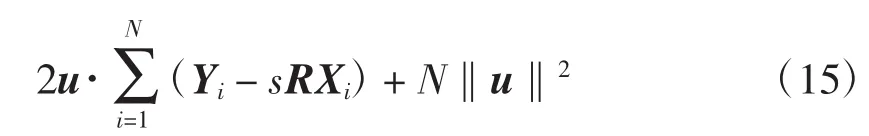
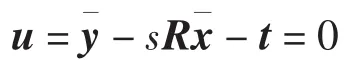
因此,可得平移向量的估计公式

误差函数可简化如下
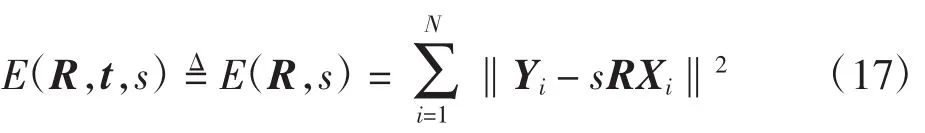
2.3 姿态估计的Cayley方法
由于旋转矩阵给出等距变换,可得‖RXi‖=‖Xi‖。因此当范数‖Xi‖和‖Yi‖已知时,可按下式来估计尺度因子

然后将式(7)代入式(13),可得

最后根据式(7)估计旋转矩阵R。于是可得姿态变换参数的最优解为
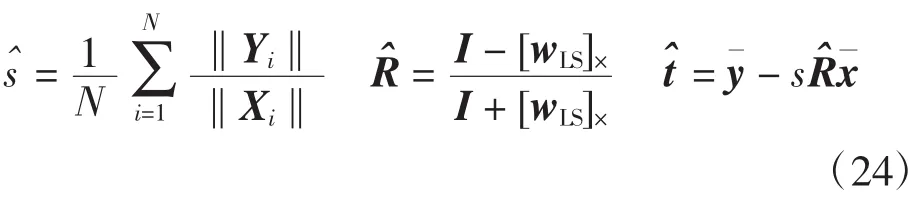
已知尺度因子的估计值,式(19)便可写成


由式(20)与式(21)可得方程组
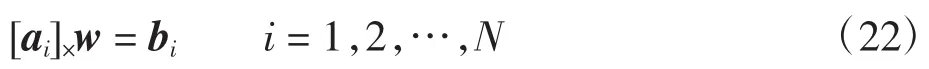
解得w的最小二乘解为
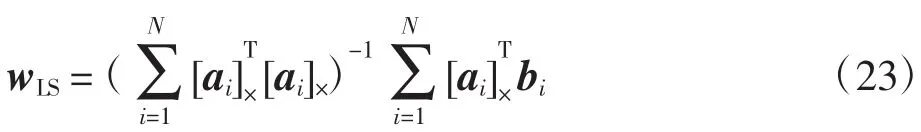
基于Cayley变换的三维点云配准算法总结如下:
算法1三维点云配准矩阵估计的闭式算法。
Ensure:摄像机运动的位姿变换参数(R,t,s)
4)利用式(23)计算R的Cayley向量wLS
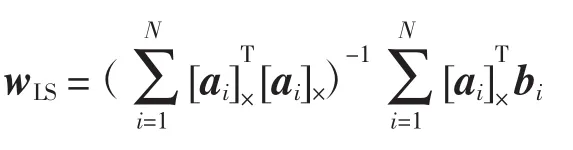
3 实验结果及分析
仿真实验采用的数据来自于Vtk库[19]中的三维恐龙状点云数据集,点数目N=10 755。随机生成姿态变换参数(R,t,s),对原始数据集进行三维相似变换,变换后的点云集记为。为验证算法1,姿态变换参数设定如下

原始点云如图2(a)所示。仿真中,为两组点云添加均值为0,标准差分别为3.721 1m和3.490 8m的高斯噪声,得到新点云,如图 2(b)所示。
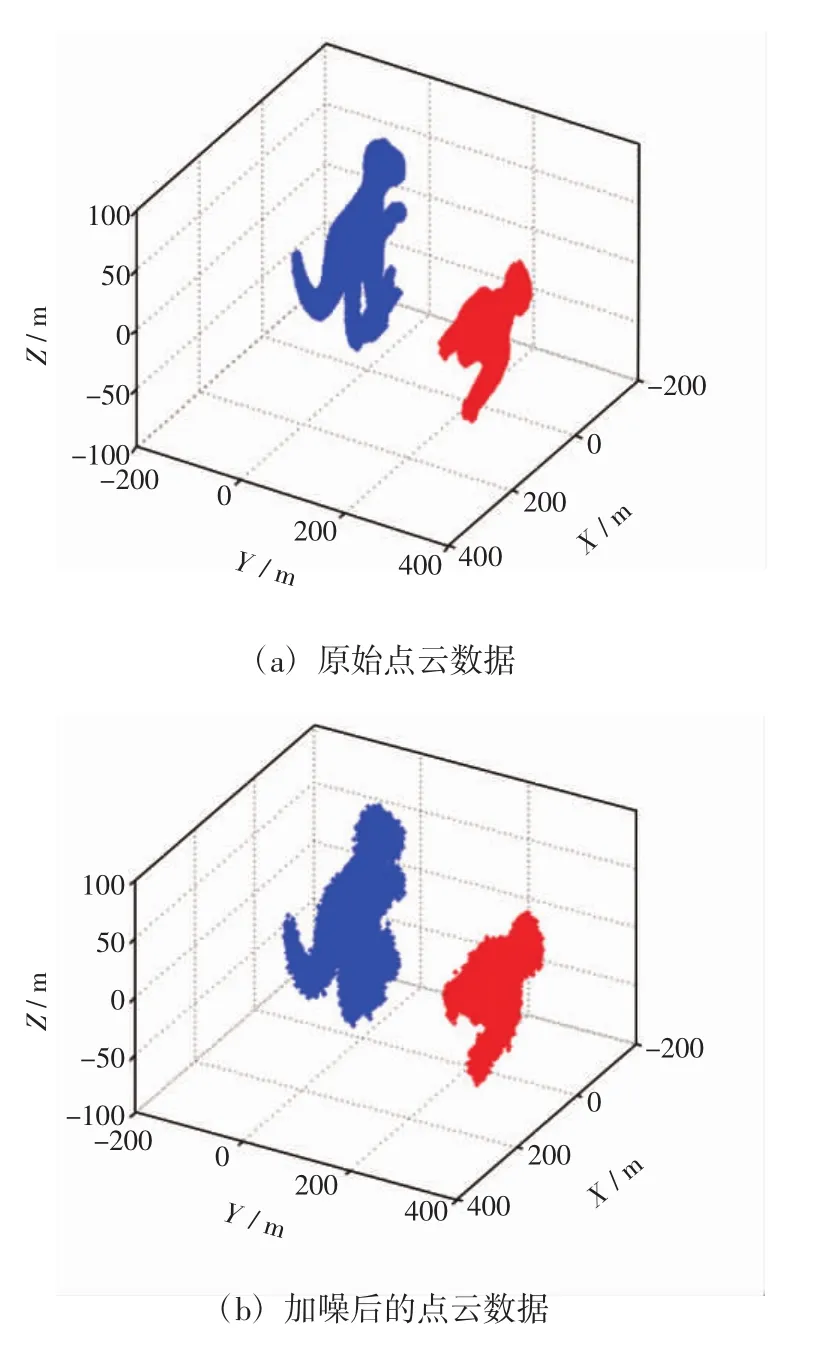
图2 加噪前后的三维对应点表示Fig.2 Description of pointpairs
1估计点云配准矩阵S^,得到姿态变换参数

从旋转矩阵的误差和平移距离误差来进一步分析算法1的位姿估计精度。旋转矩阵角度的误差计算定义为

图3 一组含噪三维对应点的匹配结果Fig.3 Registration of 3D correspondence with noise
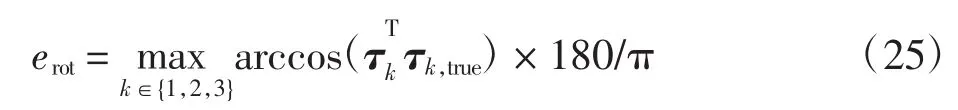
其中:τk是旋转矩阵R的第k列。平移向量估计值与真实平移向量的距离被定义为平移距离误差,即
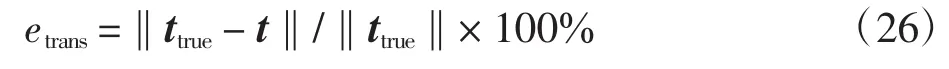
考虑Cayley方法的鲁棒性和准确性,进行多组独立的实验。设定不同尺度因子s并随机生成变换参数(R,t),然后对初始点云进行相似变换并生成多组三维对应点,添加与实验示例相同强度的高斯噪声。接着用Cayley方法估计姿态变换参数,最后计算估计误差,所得结果如图4所示。

图4 Cayley方法的姿态估计误差Fig.4 Error of estimated posevia Cayley approach
由图4可知,在不同变换参数条件下,利用Cayley方法计算出的旋转角度误差不超过2°,平移估计相对误差小于0.05%,这说明Cayley方法的位姿变换参数估计误差小、精度高。
考虑点云配准的准确性,计算配准后的两组点云的平均距离为
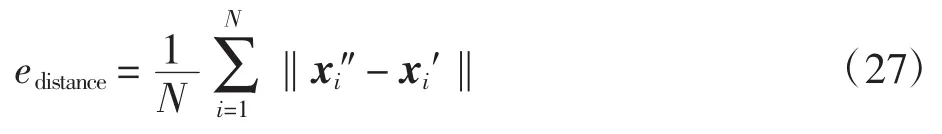
同样,随机设定变换参数(R,t,s)生成 50组三维对应点,添加的噪声强度保持不变。然后采用算法1对三维点云进行配准,最后计算配准后的点云集之间的平均绝对误差edistance=5.734m。已知实验采用的点云集规模是89.64m×197.62m×166.94m,且每组对应点分别加了标准差为3.721 1m和3.490 8m的高斯噪声。在此实验条件下,配准后的点云集之间的绝对误差在可接受范围内。
4 结语
针对SLAM中的地图点云尺度漂移问题,本文提出了利用Cayley变换来估计三维对应点之间的相似变换的闭式配准算法,从而确定相邻两帧图像的摄像机姿态变换矩阵。该算法是一个直接提供位姿变换参数最优解的闭式算法,无须迭代与校正,计算效率高,对SLAM的实时性至关重要。另外,该方法采用三维向量来表达姿态矩阵中的旋转矩阵,在仅有3个对应点的情况下便可提供线性解,而且其算法结构比较简单,容易实现。
同时,本文进行了多组随机并独立的仿真实验,通过误差分析来说明基于Cayley变换的闭式算法在三维点云配准问题中的优越性。实验结果表明,无论是旋转矩阵误差、相对平移误差还是配准后的点云集之间的距离误差都比较小,进而证实了该算法具有较高精度和较强的鲁棒性。
最后要强调的是,基于Cayley变换的闭式配准算法的适用性较广,不仅可以解决SLAM系统的点云配准问题,而且适用于计算机视觉和机器人学中的三维重建与三维拼接问题[17-18]。
[1]HARALICKRM,JOOH,LEECN,et al.Poseestimation from corresponding point data[J].Machine Vision for Inspection&Measurement,1989,19(6):1-84.
[2]BESLPJ,MCKAYND.Method for registration of 3D shapes[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1992,14(2):239-256.
[3]HENRY P,KRAININM,HERBSTE,etal.RGB-D mapping:using Kinect-style depth cameras for dense 3D modeling of indoor environments[J].International Journal of Robotics Research,2012,31(5):647-663.
[4]HARTLEY R,ZISSERMAN A.Multiple View Geometry in Computer Vision[M].2nd ed.Cambridge:Cambridge University Press,2003.
[5]王忠立,赵 杰,蔡鹤皋.大规模环境下基于图优化SLAM的图构建方法[J].哈尔滨工业大学学报,2015,47(1):75-85.
[6]顾照鹏,刘 宏.单目视觉同步定位与地图创建方法综述[J].智能系统学报,2015(4):499-507.
[7]IZADIS,NEWCOMBE R A,KIM D,et al.Kinect Fusion:Real-time Dynamic 3D Surface Reconstruction and Interaction Using a Moving depth Camera[C]//International Conference on Computer Graphics and Interactive Techniques,Santa Barbara,CA,Oct 16-19,2011:1175-1184.
[8]RAULM A,MONTIEL JMM,JUAND T.ORB-SLAM:a versatile and accurate monocular SLAM system[J].IEEE Transaction on Robotics,2015,31(5):1147-1163.
[9]ARUN K S,HUANG TS,BLOSTEIN SD.Least-squares fitting of two 3-D point sets[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1987,9(5):698-700.
[10]HORNBKP,HILDENHM,NEGAHDARIPOURS.Closed-form solution of absoluteorientation using orthonormal matrices[J].Journal of the Optical Society of America A,1988,5(7):1127-1135.
[11]HORN B K P.Closed-form solution of absolute orientation using unit quaternions[J].Journal of the Optical Society of America A,1988,4(4):629-642.
[12]WALKERMW,SHAOL,VOLZRA.Estimating3D location parameters using dualnumber quaternions[J].CVGIP:Image Understanding,1991,54(3):358-367.
[13]EGGERTDW,LORUSSO A,FISHER R B.Estimating 3D rigid body transformations:a comparison of four major algorithms[J].Machine Vision and Applications,1997,9:272-290.
[14]WU Fuchao,WANG Zhiheng,HU Zhanyi.Cayley transformation and numericalstability of calibration equation[J].International Journal of Computer Vision,2009,82(4):156-184.
[15]CAYLEYA.Sur quelques proprietes des determinant gauches[J].Journal Fur Die Reine Und Angewandte Mathematik,1846(32):119-123.
[16]吴福朝.计算机视觉:Cayley变换与度量重构[M].北京:科学出版社,2011.
[17]张鸿燕.基于视频图像的三维建模方法与系统——消化道三维建模方法与应用研究[D].北京:中国科学院研究生院,2011.
[18]周璐莎.大尺度场景的同步定位与地图构建 [D].天津:中国民航大学,2016.
[19]A Small Program for Rendering a Point Cloud UsingVTK[EB/OL].[2017-06-14].http://www.umiacs.umd.edu/~huytho/codes.htm.
Cayley approach for 3D points registration in visual SLAM
ZHANG Hongyan,WANG Jingyan,ZHOU Lusha,WANG Binghui
(Sino-European Institute of Aviation Engineering,CAUC,Tianjin 300300,China)
An essential problem in SLAM system is to compute the 3D rigid body transformation of cameras,which aligns two sets of points when correspondences are known.The errors accumulated during the locating and mapping process result in the drift of scale for the pairs of points.The Euclidean transformation will be degraded into the similarity transformation due to the drift.A closed-form solution using Cayley transform is presented to estimate the similarity transformation between 3D corresponding points.The accuracy and robustness of the proposed Cayley approach are verified by simulation and error analysis.Apart from SLAM system,this approach is also suitable for3D reconstruction and registration in computervision.
SLAM;3D registration;similarity transformation;Cayley transform
张鸿燕(1978—),男,湖南岳阳人,讲师,博士,研究方向为计算机视觉.
TP391;V219
A
1674-5590(2017)05-0047-05
2017-01-10;
2017-02-23
国家自然科学基金项目(U1633101);中央高校基本科研业务费专项(ZXH2012H005);国家级大学生创新创业训练计划项目(201510059038)
?
刘佩佩)

