基于不确定随机需求的周期性库存策略

张春晓，李润辉

（中国民航大学理学院，天津 300300）

基于不确定随机需求的周期性库存策略

张春晓，李润辉

（中国民航大学理学院，天津 300300）

经典的周期性库存模型中通常将需求视为随机变量，然而在生产实践中，当设备如民用飞机更新后由于缺乏历史运营数据，无法得到其零部件需求的分布函数。因此企业决策新设备零部件库存问题时通常会参考原设备的失效数据，并邀请相关领域专家给出新设备零部件需求的主观信度。为刻画新设备对该零件需求的随机性和主观不确定性，引入机会理论将需求假设为不确定随机变量，建立周期性订货优化模型，推导出使利润最大化时最优订货策略的解析解。最后，用数值算例验证该模型的可行性，并对各参数进行了敏感性分析。

周期性库存；不确定随机变量；机会理论；新设备需求

?

周期性订货策略是零售商通常采用的库存策略之一，其决策变量为固定周期内的最优订货量，即根据每一盘点周期商品销售量的变化而制定最佳的订购数量。现有文献中经典的周期性订货策略大都假定设备需求是一个常数或随机变量，基于概率论收集足够的历史销售数据，为需求分布函数做一个合理估计。

较早的周期性订货策略研究是1990年威尔逊[1]所建立的经济订货批量模型，其假设商品需求率连续均匀且为常数，给出了不允许缺货情形下的最佳订货批量公式，之后该模型被扩充为允许缺货的模型。2001年，York等[2]研究了设备需求率和供应商的生产率均为常数的多阶段订货模型并证明了订购成本的投资越小，订购周期越短，订货商的订购批量和滞后供给量越小。2002年罗兵等[3]研究了需求和订购周期均为随机变量、需求率为线性递增函数的模型，并推导出了最优订购批量、最优订购周期等的解析式。2004年，Dominey[4]提出了一种单个顾客需求为独立随机变量、整体需求近似服从复合泊松分布的单周期库存模型，并对模型的最优解做出了分析。2006年，Berman和Perry[5]建立了需求为随机变量且库存水平为指数函数条件下的周期性库存模型，对模型最优解进行了讨论，并给出了数值算例和灵敏度分析。

考虑某企业为更换新设备，需制定维护新设备所需零部件的库存策略，然而由于缺乏历史运行数据，难以获得新设备对某零部件的需求概率分布函数。假定该零部件在原有设备的需求概率分布可通过历史销售数据获得，对新设备中该零部件的未来需求则邀请专家给出其主观信度，这时原设备需求的随机性和新设备专家信度的主观不确定性同时出现在库存系统中，如果仅将需求作为随机变量用概率论知识来处理，就不能够得到合理的结果。

实际工作中常常缺乏观测数据，或暂时无法获得足够观测数据，研究者通常邀请该领域专家给出主观信度。为了合理解决对主观信度的数学建模，2007年Liu[6]创立了不确定理论，定义了不确定测度和不确定随机变量，并在此基础上发展出不确定规划、不确定随机规划等。2009年，Qin等[7]将不确定理论引入单周期库存问题，把设备需求当作一个不确定变量，给出了利润最大化的最佳库存量。基于这个研究，Gao[8]又将不确定理论引入经典报童问题中，得到了最佳订货量的解析解。

随着不确定理论的发展，为了描述随机性和不确定性同时存在于一个复杂系统中的现象，研究者相继开创了机会理论并定义了不确定随机变量，引入了机会测度用以描述不确定随机变量并给出不确定随机变量的机会分布以及不确定随机变量的运算法则等[9-12]，之后许多学者对机会测度及不确定随机变量的数字特征进行了研究。目前，机会理论也取得了一定的应用成果。

在之前学者研究的基础上，将考虑某产品的新设备订货策略，假定需求为不确定随机变量，应用机会理论建立周期性订货模型。通过研究目标函数的性质，对模型进行求解并给出订货量应满足的最优条件，最后应用到实际问题中证明其可行性。

1 预备知识

本节简要介绍文中用到的不确定理论和机会理论的基础知识[11]。

令Γ是一个非空集合，L是Γ上的σ-代数。σ-代数L中每个元素Λ称为事件，不确定测度是从L到[0，1]的函数。为了公理化定义不确定测度，有必要给出每个事件Λ的测度值Μ{Λ}，此测度Μ{Λ}是事件Λ可能发生的信度。为了合理给出专家信度，Liu提出如下3条公理：

公理1（正则性）对于全集Γ，有Μ{Γ}=1。

公理2（对偶性）对于任何事件Λ，有Μ{Λ}+Μ{Λc}=1。

公理3（次可加性）对于任意可数事件序列Λ1，Λ2，…，有

定义1令Γ是一个非空集，L是Γ上的σ-代数，Μ是不确定测度，则三元组（Γ，L，Μ）称为不确定空间。

定义2不确定变量ξ是从不确定空间（Γ，L，Μ）到实数集的可测函数，即对任意的Borel集B，集合

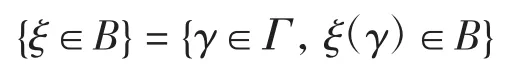
是事件。

定义3对于任意的实数x，不确定变量ξ的不确定分布定义为

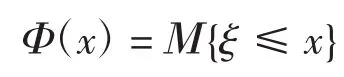
定义4一个不确定变量ξ被称为是线性的，如果它有一个线性不确定分布记为 L（a，b），a和 b 为实数，且 a＜ b。

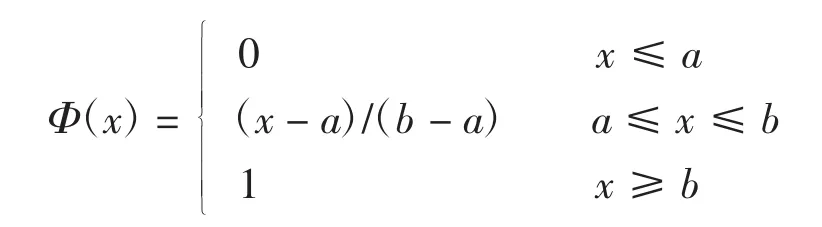
定义5令ξ是不确定变量，则ξ的期望值定义为

条件是如上两个积分中的至少一个是有限。

定义6不确定分布Φ被称为是正则的，如果对每一个α∈（0，1），其逆函数Φ-1（α）存在且唯一。

定义7令ξ是一个不确定变量且具有正则不确定分布，则逆函数Φ-1称为ξ的不确定逆分布。

定理1令ξ是不确定变量并具有正则不确定分布Φ。如果期望值存在，则

定义 8令（Γ，L，Μ）× （Ω，A，Pr）是机会空间，再令Θ∈L×A是一个事件。则机会测度Θ定义为

定义9令ξ是一个不确定随机变量。则ξ机会分布定义为

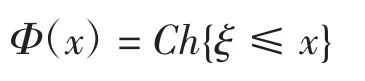
定理 2令 η1、η2，…，ηm是独立的随机变量，概率分布分别是 Ψ1、Ψ2，…，Ψm，并令 τ1、τ2，…，τn是独立的不确定变量，不确定分布分别是 Φ1、Φ2，…，Φn，则不确定随机变量

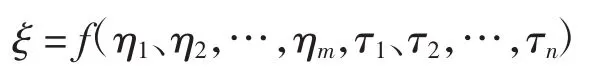
有期望值

其中：f（η1、η2，…，ηm，τ1、τ2，…，τn）对于τ1、τ2，…，τn是单增函数或单减函数。

2 假设和符号

本文研究某产品在新设备中固定周期内的订货策略，为了建模方便，给出以下假设和符号。

2.1 符号

ξ为原设备中零部件的需求，随机变量；η为新设备中零部件的需求，不确定变量；γ为总需求，不确定随机变量，且γ=η+ξ；Q为订货量，决策变量；P为单位售价；C为单位存储费用；K为单位成本；W（Q，γ）为总利润函数。

2.2 假设

①P，C，K为已知常数；②在原设备中和新设备中该零部件需求相互独立；③允许缺货，缺货时只有收入损失，没有其他费用损失；④存储费用为正数，且P＞K＞0；⑤库存没有限制。

3 模型

假设原设备中某零部件需求ξ的概率分布可通过历史数据获得，新设备中需求η可通过专家信度给出不确定分布，这时不确定变量和随机变量同时出现在周期性订货策略中，即总需求是一个不确定随机变量γ=ξ+η。通常情况下，建立库存问题的目标函数有两种方法：一种是以整个系统库存成本期望值最小为目标函数；另一种是以总利润期望值最大为目标函数。本文采用第2种方法来建立目标函数。

根据模型假设，该产品在一个周期内的销售利润为

因为设备需求γ是一个不确定随机变量，所以W（Q，γ）作为不确定随机变量γ的函数也是一个不确定随机变量，又利润函数式（2）对于不确定变量γ是单调的增函数。因此，可根据机会理论式（1）求得W（Q，γ）的期望值，即平均利润。为了最大化利润期望值，寻求最优订货量Q*，给出定理3。

定理3假设γ是一不确定随机变量，且γ=ξ+η，其中ξ是一随机变量且服从概率分布Ψ，η是一不确定变量且服从不确定分布Φ，定义函数W（Q，ξ+η）为

则W（Q，ξ+η）的期望值为

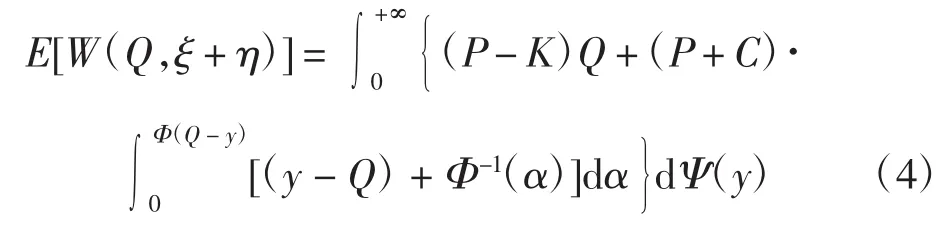
证明因为ξ+η是一个不确定随机变量，且W（Q，ξ+η）对于不确定变量η是单调增的，根据定理2，有

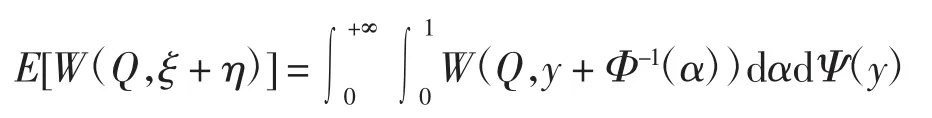
其中

因此

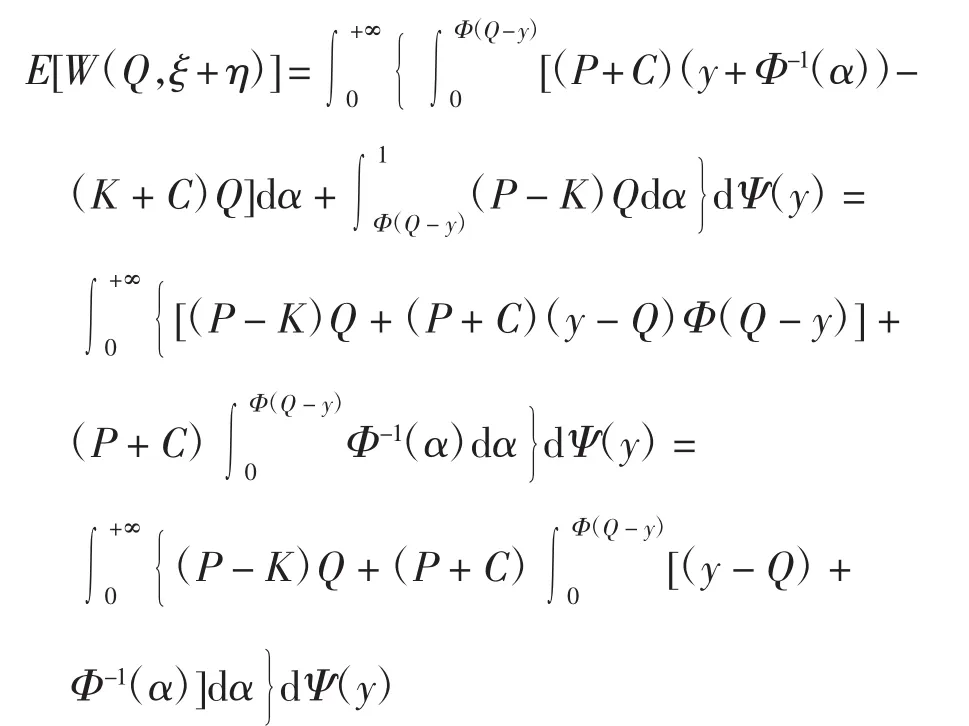
定理证毕。

定理4设Q为决策变量，γ是不确定随机变量，且γ=ξ+η，其中ξ是一个随机变量且服从概率分布Ψ，η是一个不确定变量且服从不确定分布Φ，对于不确定随机规划模型

其最优解Q*满足

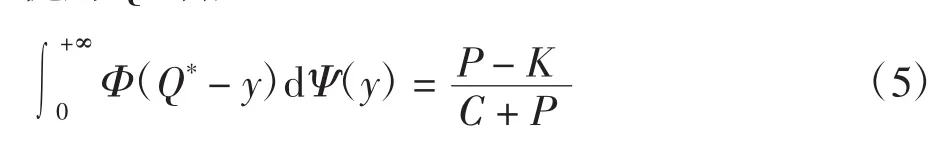
证明目标函数对Q求导，得

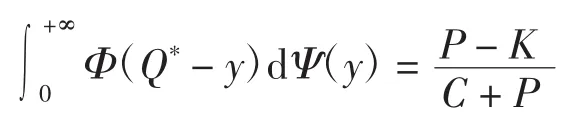
若Q≤Q*时，E[W（Q，γ）]≥ 0；而当Q＞Q*时，E[W（Q，γ）]＜0。所以目标函数是关于Q的凹函数，则Q*是最优订货量。

定理证毕。

4 算例

航材订购是保证飞机正常运营的必要条件，航材储备量过低或过高都会影响飞机的安全性和经济性，过低的储备无法应付突发事故，过高的储备又会增加管理方面的人力和物力，且经费不允许。因而，必须确定合理的航材储备标准并做好航材储备管理工作。算例采用某航空公司航材部订购新引进国产大飞机所用某种型号螺栓的订货问题，假设该螺栓在相似机型的需求量是一个随机变量并服从指数分布，即

新型飞机的需求量是一个不确定变量并服从线性不确定分布L（a，b）[12]，即

将式（6）和式（7）代入定理 4的式（5），得到最优订货量Q*的表达式为

假定每个螺栓的存储费为C=2，每个螺栓成本K=6，每个螺栓售价P=20，a=100，b=800，λ =0.01，则最优订货量Q*如图1所示。

从图1可以看出，模型中的各参数对最优订货量都有显著影响。随着单位货物成本的增加，最优订货量减小。由图1（a）可知，在单位货物售价增加的情况下，最优订货量增加。即货物售价提高，公司利润会增加，从而最优订货量也要增加。由图1（b）可知，随着单位货物存储费的增加，最优订货量在减少。由图1（c）中可以看出，随着参数λ的增大，最优订货量在减少。因为在原来设备中，需求服从指数分布，参数λ的增加会导致需求的减少，因此最优订货量也会随着减少。从图1（d）可以看出，最优订货量随着b的增大而增大，也就是对于固定的a，最优订货量随着b-a的增大而增大。即在新的设备中，参数b-a增大，需求也会

图1 不同参数下的最优订货量Q*Fig.1 Optimal order quantity Q*for increasing values of P，C，λ，b

随着增大，从而增加最优订货量。

5 结语

在不确定随机需求的情况下，对周期性订货问题进行了研究，主要结论如下：

1）由于缺乏历史数据，将总设备需求设为不确定随机变量，引入机会理论，即随机性和不确定性同时出现在库存问题中，建立了周期性订货策略的库存模型。

2）以平均利润最大为目标函数建立了周期性订货的数学模型，通过对不确定随机需求下的库存模型进行求解，得出相应的最优订货策略的表达式。

3）算例分析验证了模型的有效性和可行性，结果可为决策者在新设备中某零部件的库存问题提供参考。

由于缺乏历史数据，不确定随机需求下的周期性库存策略模型将有助于解决实际问题，并可被扩充到多个阶段多产品的库存问题，这有待于进一步研究。

[1]运筹学教材编写组.运筹学(修订版)[M].北京:清华大学出版社,1990.

[2]YORKYW,HSUShulu,WUSoushan.An integrated inventory model for a single vendor and multiple buyer with ordering cost reduction[J].Production Econmics,2001,73(3):203-215.

[3]罗 兵,杨秀苔,熊中楷.随机状态下需求均值为线性函数时的EOQ模型[J].重庆大学学报（自然科学版）,2002,25(5):131-135.

[4]DOMINEY M J G,HILL R M.Performance of approximations for compound Poisson distributed demand in the news boy problem[J].International Journal of Production Economics,2004,92(2):145-155.

[5]BERMANO,PERRY D.An EOQ model with state-dependent demand rate[J].European Journal of Operational Research,2006,171(1):255-272.

[6]LIU Baoding.Uncertainty Theory[M].2nd ed.Berlin:Springer,2007.

[7]QIN Z F,KAR S.Single-period inventory problem under uncertain environment[J].Applied Mathematics and Computation,2013,219(18):9630-9638.

[8]DINGSibo,GAO Yuan.The(σ,s6,smath container loading mathjax)policy for uncertain multi-product newsboy problem[J].Expert systems with Applications,2014,41(8):3769-3776.

[9]LIU Baoding.Uncertainty Theory:A Branch of Mathematics for Modeling Human Uncertainty[M].Berlin:Springer Publishing Company,2010.

[10]LIU Yuhan.Uncertain random variables:Amixture of uncertainty and randomness[J].SoftComputing,2013,17(4):625-634.

[11]LIU Yuhan.Uncertain random programming with applications[J].Fuzzy Opti-mization and Decision Making,2013,12(2):153-169.

[12]LIU Baoding.Why is there a need for uncertainty theory[J].Journal of Un-certain Systems,2012,6(1):3-10.

Periodic inventory policy based on uncertain random demand

ZHANG Chunxiao,LI Runhui
（College of Science,CAUC,Tianjin 300300,China）

In classic periodic inventory model,demand is usually considered as a random variable,but in production practice,the distribution function of new equipment demand cannot be obtained due to lack of historical sale data.So companies usually take product demand data of the original equipment as reference,and invite relevant experts to provide a subjective estimate to the unit demand distribution of new equipment.To describe the randomness and subjective uncertainty of the new equipment demand，chance theory is introduced and the demand is assumed as a uncertain random variable.A periodic order optimization model is built and an optimal analytical solution for profit maximization is obtained.Finally, numerical examples verify the feasibility of the current model,and a sensitivity analysis for parameters is taken.

periodic inventory;uncertain random variable;chance theory;new equipment demand

张春晓（1971—），女，青海西宁人，教授，硕士，研究方向为民航统计与优化.

O227

A

1674－5590（2017）05－0056－04

2016-12-08；

2017-02-22

中央高校基本科研业务费专项（3122016D030）

?

刘佩佩）