基于Simulink变论域算法仿真技术研究
吕旭旭,邵天章,谷志峰
(1.陆军工程大学石家庄校区,河北 石家庄 050003;2.石家庄铁道大学,河北 石家庄 050043)
1 引言
单相逆变器输出电压质量的提高一直是领域内研究热点,工程中常用控制策略有电压单闭环、电压电流双闭环控制、重复控制等,研究表明传统控制算法均能提高逆变器的输出电能质量,但在谐波含有量,动态响应等性能上仍存在问题[1-5]。近年随着智能控制理论的发展为解决上述问题提供了新的思路。在这些智能控制中,模糊控制被证明是一种可靠有效的方法,但在应用过程中受固定论域限制而导致模糊规则利用率大大降低,造成控制精度不高[6]。为解决这一问题,李洪兴教授首次提出变论域的概念,变论域算法通过对语言变量论域的改变大大增加实际控制规则,有效提高了控制精度,并利用此控制方法取得了四级倒立摆的控制成功,此举更加充分证明了变论域模糊控制算法的优良性[7-9]。
在研究变论域算法的控制效果时,借助Simulink工具对其仿真验证是必要且重要的,文献10指出Simulink 只提供常规模糊控制工具箱,无法支持变论域模糊控制算法,只有通过 S-函数扩展 Simulink 的功能才能实现其仿真,这是极其不方便的。文献11-13均利用模糊控制工具箱对变论域模糊控制算法进行仿真,但缺少如此仿真的理论依据和支撑,仿真结果虽优,但无法从理论说明此建模的正确与否。对此,本文用模糊数学理论,从理论层面为借助Simulink常规模糊控制工具箱对变论域算法的仿真提供支撑,为变论域算法的仿真研究做以补充。为验证文中理论,将其应用在单相逆变装置的控制仿真研究,仿真结果良好,证实了本文所得结论的正确性。
2 固定论域模糊控制器的插值原理
2.1 SISO系统定论域模糊控制器插值原理
对于一个SISO系统,假设其输入输出分别为X,Y,论域分别为[-EX,EX],[-EY,EY]。记MFX={Ai}(1≤i≤n),MFY={Bi}(1≤i≤n),其中MFX,MFY分别是X和Y实区间论域上的模糊集合,其上的模糊集{Ai}(1≤i≤n),{Bi}(1≤i≤n)为各自论域上的一组基元组,若无另外说明,文中各模糊集均采用三角形隶属度函数,各模糊集中心均在论域上且等距划分,输入输出推理规则为
R(i):IFxisAiTHENyisBi
(1)
并根据Mamdani含义解释R(i),则此系统的输入到输出的映射关系可以用下面的插值函数来描述[14]
(2)
其中μAI为模糊集Ai的隶属度函数。
2.2 MISO系统定论域模糊控制器插值原理

R(j):IFx1isA1j&…&xnisAnj
THENyisBjj=1…m.
(3)
其中m=n1·n2·…·nn,对于每一个规则均可以采用单输入输出的插值机理来合成,保持 Mamdani含义解释各个规则,采用中心平均解模糊器方法计算输出,则据式(2)可得
(4)
其中μAij为模糊集Airi的隶属度函数。

(5)
至此推导出固定论域多输入单输出系统的插值函数。
3 SIMO系统变论域模糊控制器的插值原理

(6)
(7)

(8)
即通过伸缩因子,可使输入输出的论域随输入输出相应的收缩或膨胀,论域的改变也导致相应论域上各模糊集的隶属度函数形状发生改变。
采用变论域算法时,模糊控制器的形式也要随之改变,即用伸缩因子改变了的论域和相应隶属度函数改写式(5)得
(9)

(10)
又各个模糊集采用三角隶属函数,其中心均在论域上且等距划分,则对于第k次采样时刻有
(11)
由式(11)可易得
(12)
将式(12)代入式(9)中可得

(13)
至此推导出变定论域多输入单输出系统的插值函数。


图1 伸缩因子两种作用形式示意图
Simulink的模糊控制工具箱论域设定好不能实时改变论域的大小,通过以上分析可知,保持固定论域,将伸缩因子的作用向输入输出移动与真正改变论域可等效,从而为利用Simulink的模糊控制工具箱仿真变论域算法提供理论支持。
4 仿真验证
为验证理论研究和文中结论,在Simulink中设计单相逆变器的控制仿真。其中单相逆变器采用全桥结构,后级加LC滤波单元,其主电路图如图2所示。

图2 单相全桥逆变主电路
单相逆变器常用PID控制电压输出,其谐波含有量较高,近年模糊控制+PID的组合算法可以提高其性能,但传统模糊控制在误差较小时规则使用率低,控制性能不高,本文采用变论域模糊控制+PID的组合算法实现对其输出电压波形的有效控制。变论域算法在前文已有详细介绍,其伸缩因子的形式多种多样[15],本文采取模糊推理型伸缩因子,整体算法控制框图如图3所示。
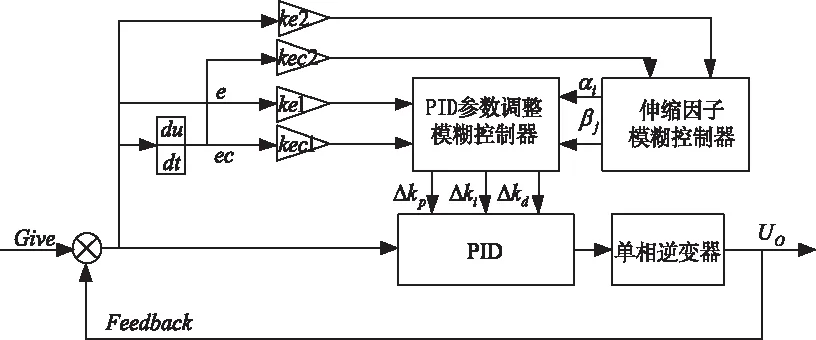
图3 变论域模糊控制+PID组合算法控制框图
图中输入量为误差e和误差变化率e′,伸缩因子模糊控制器输出为
αi,βj(i=e,ec;j=kp,ki,kd)
(14)
PID参数调整模糊控制器的输出为Δkp,Δki,Δkd,图中kei,keci(i=1,2)为输入量化因子,其将真实值映射到模糊控制的基础论域,各输出的比例因子未在图中标识,其为
kαi,kβj,km(i=e,ec,j=m=kp,ki,kd)
(15)
比例因子作用与量化因子刚好相反。最终PID控制器的参数为
(16)
模糊控制器设计所有隶属度函数均为对称三角形;输入变量e和e′的论域均设定为[-6,6],在其上定义NB、NM、NS、ZO、PS、PM、PB7个模糊集,其中心对应-6,-4,-2,0,2,4,6;伸缩因子模糊控制器输出αi,βj(i=e,ec;j=kp,ki,kd)的论域设定为[0,1],其上定义VVS,VS,S,H4个模糊集,中心对应0,0.33,0.66,1;PID参数调整模糊控制器输出Δkp,Δki,Δkd的论域设定为[-6,6],在其上定义NB、NM、NS、ZO、PS、PM、PB 7个模糊集,其中心对应-6,-4,-2,0,2,4,6。
各推理规则根据工程控制经验确定,以αe和Δkp的控制规则为例,给出规则表如表1所示。

表1 αe和Δkp的控制规则表
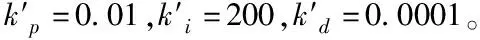
(17)
逆变主电路参数:滤波电感Lf=0.8Mh,滤波电容Cf=20μF,采用单极倍频调制方式,开关频率fs=25.6kHz,标准给定正弦幅值230V,频率50Hz;由以上参数搭建算法仿真模型如图4所示。

图4 变论域模糊控制+PID组合算法系统模型
图中黑色虚框是算法的模型实现部分,其被封装在一个子系统中,箭头标注了其内部结构。仿真采用对比法,将传统PID、定论域模糊控制+PID、变论域模糊控制+PID控制三种算法的控制效果进行对比。设置仿真时长0.3s,且均在0.1s投入1KW+2KVar的感性负载,0.15s切除,三种算法的仿真结果波形如下所示。
从实验波形可以看出,在突加负载时传统PID控制、固定模糊控制+PID、变论域模糊控制+PID的瞬态电压跌落分别为2.71%,2.03%和1.54%,其总谐波畸变率分别为2.44%,1.77%和1.07%,说明变论域模糊控制+PID算法具有良好的控制性能,表明了使用Simulink模糊控制工具箱搭建变论域算法仿真模型的正确性,验证了2,3两节的理论说明和分析。
5 结论
变论域模糊控制器作为一种高精度自适应模糊控制器,被广泛应用到各个行业,为了更好的工程实现,对其进行仿真是必要的。已有大量文献借助Simulink模糊控制工具箱对变论域算法进行仿真,但如此的仿真形式缺乏一定理论支撑。本文以严格的数学推导和详实理论分析为通过Simulink模糊控制工具箱仿真变论域模糊控制算法提供了理论依据和方法,并以单相逆变电源为例,在Simulink中搭建变论域模糊控制+PID算法仿真模型。仿真结果表明其具有良好的静动态性能,证实了本文所提理论依据和方法的正确性。

图5 传统PID,定论域模糊控制+PID,变论域模糊控制+PID算法输出电压及FFT分析波形

