芯层可压缩的夹层梁动态刚度矩阵研究

王海英，张桂勇

（1.大连海洋大学 航海与船舶工程学院，辽宁 大连116023；2.大连理工大学 船舶工程学院，辽宁 大连 116024）

芯层可压缩的夹层梁动态刚度矩阵研究

王海英1，张桂勇2

（1.大连海洋大学 航海与船舶工程学院，辽宁 大连116023；2.大连理工大学 船舶工程学院，辽宁 大连 116024）

该文推导了考虑芯层垂向压缩变形影响的夹层梁的动态刚度矩阵，为动态刚度矩阵方法提供了一种新的单元类型。首先给出了一种考虑夹层梁芯层垂向压缩变形影响的夹层梁位移模式，推导了相应的夹层梁动能和势能，根据Hamilton原理推导了其控制微分方程，按动态刚度矩阵的一般推导过程推导了考虑芯层垂向压缩变形影响的夹层梁动态刚度矩阵。计算结果表明文中推导的夹层梁动态刚度矩阵是正确可靠的；在夹层梁的动态刚度矩阵推导和高频振动计算中考虑芯层垂向压缩变形是合理的。

动态刚度矩阵；夹层梁；固有频率

0 引 言

夹层梁是一种由金属面板及粘弹性材料芯板所组成的复合结构，具有比重量轻、比强度大的力学优点，广泛应用于对材料重量和强度要求较高的航空航天、舰船等工程领域，其动态特性研究受到广泛关注，且理论趋于成熟。

动态刚度矩阵法是源于但优于有限元法的一种解决结构动力问题的计算方法，它尤其适合于对精度要求较高的高阶的结构动力分析问题。同有限元方法一样，在夹层梁动态刚度矩阵研究中首先建立合理有效的结构简化模型是解决问题的关键。但这种方法不受单元数量和精度的限制，只需对结构划分极少数单元就可以得到结构精确解，甚至通过单一的结构单元就可以在保证精度条件下得到结构任意阶的固有频率，而这在一般有限元方法中是不能实现的。虽然早期学者在动态刚度矩阵研究中已经取得了显著成果，但是针对夹层梁等复合结构的动态刚度矩阵方法研究还存在相当的难度。Banerjee[1]首先将动态刚度矩阵方法应用于夹层梁的动态特性研究中，并逐渐完善。在其早期研究中，夹层梁的上下面板被简化成Bernoulli-Euler梁，即只考虑抗弯作用，而芯层则只起到抗剪作用。Howson和Zare[3]也在这种模型假设下进行了夹层梁的动态刚度矩阵研究，但这种模型只适合求解低频问题。随后Banerjee和Sobey[2]又对该模型进行了改良，上下面板假设为Rayleigh梁，芯层则假设为Timoshenko梁，均计入了剪切变形的影响。在这基础上，Banerjee和Cheung等[4]又推导了3层均遵循Timoshenko梁理论假设的夹层梁动态刚度矩阵，并对其理论结果进行了试验验证。Banerjee和Sua等[5]又研究了计入弯曲变形和转动惯量影响的夹层梁模型的动态刚度矩阵，并将其应用到复合机翼的振动研究当中。Li和Hua等[6]用动态刚度矩阵方法分析了具有轴向载荷作用的夹层梁的动态特性，其模型计入了夹层梁的轴向载荷、轴向变形、剪切变形以及转动惯量的影响。此外，还有研究者将动态刚度矩阵推广到了板及复合板的研究当中，也取得了一定成果[7-8]。

最近有研究表明[9]，当夹层结构的芯层较厚或者分析其高频振动问题时，若不能体现芯层的垂向压缩变形的影响，则会影响结果精度。本文在前人工作基础上推导了考虑芯层垂向压缩变形的夹层梁动态刚度矩阵，其中面板考虑剪切变形的影响，芯层则同时考虑了剪切和垂向压缩两种变形的影响。首先给出了考虑芯层压缩变形影响的夹层梁控制微分方程；通过符号运算将微分方程合并成一个6阶代数特征值问题并给出解析解；根据本构关系推导出频率相关的系统动态刚度矩阵；应用Wittrick-Williams算法求解了所得自由振动动态刚度矩阵方程。通过算例表明：本文推导的夹层梁动态刚度矩阵是正确可靠的；在夹层梁的动态刚度矩阵推导和高频振动计算中考虑芯层垂向压缩变形是合理的。

1 夹层梁的控制微分方程及其解

假设一三层均为各向同性的均匀夹层梁结构，长为L，宽为b；上下面层的厚度为ti，质量密度为ρi，弹性模量为 Ei，惯性矩为 Ii；芯层的厚度为 h，密度为 ρc，弹性模量为 Ec，惯性矩为 Ic。 其中 i=1，2，分别表示上下面层，下文同。

夹层梁上下面层遵循Timoshenko梁变形假定，芯层在Timoshenko梁变形假定基础上，考虑了其垂向位移，即挠度wc沿厚度方向的变化。假定各层局部坐标原点为几何中心，垂向挠度方向为y轴，向上为正；梁轴向方向为x轴，左手坐标系统。则位移模式如下：

根据以上位移模式，推导出夹层梁的动能T及势能U，代入拉格朗日方程L=T-U，再应用Hamilton原理可得如下微分方程：

同时可得层1和层2轴向力与广义位移关系：

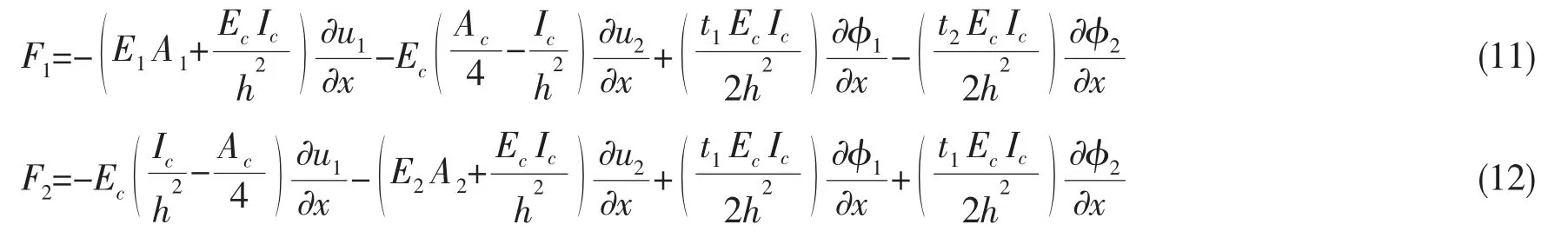
层1和层2的弯矩与广义位移关系：

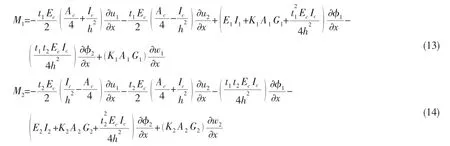
层1和层2的剪切力与广义位移关系：

假设层 1 和层 2 位移 u1、u2、φ1、φ2、w1、w2为时间的正弦函数，则可表示为：

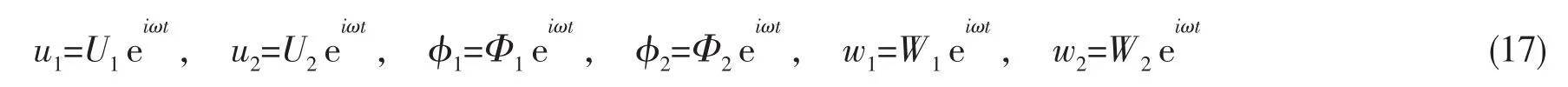
将（17）式代入（5）-（10）式，引入无量纲参数 ξ=x/L，并记 D=d/dξ，则可得到：

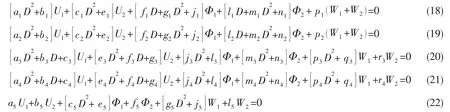
此处将位移幅值转化为指数形式：

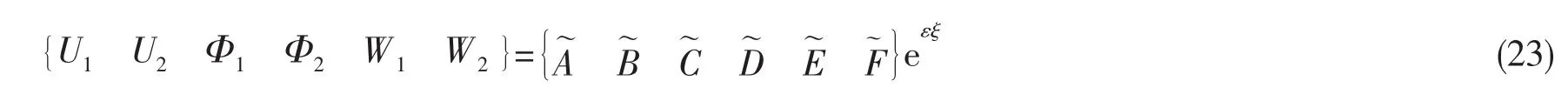
代入（18）-（22）式，令方程组的系数矩阵行列式为零，可得关于ε的12阶多项式特征值方程：

引入 λ=ε2，则上式可表示为：

方程（25）的根由一般搜根方法求得。

设 U1、U2、Φ1、Φ2、W1、W2解的形式为：

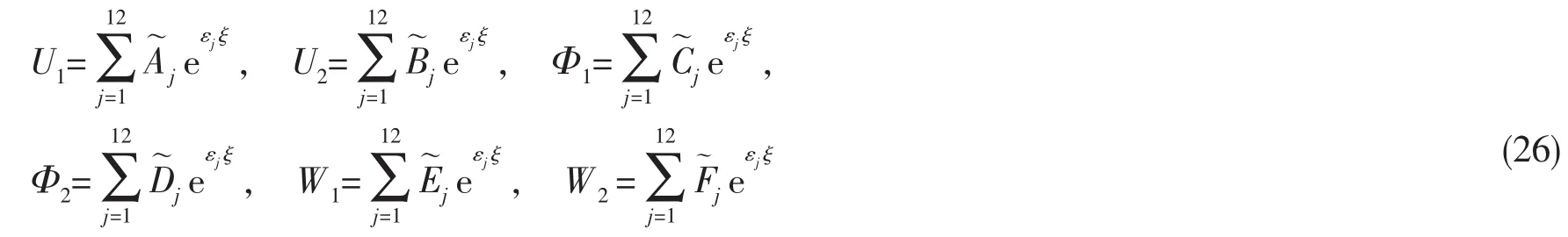
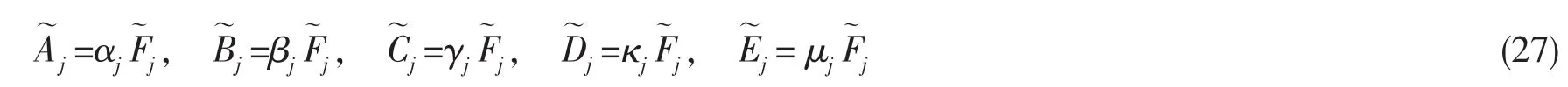
其中的系数 αj，βj，γj，κj和 μj可由下式通过 Cramer法则求得：

将（17）、（26）式和（27）式代入（11）-（16）式，并引入无量纲参数 ξ=x/L，可得：

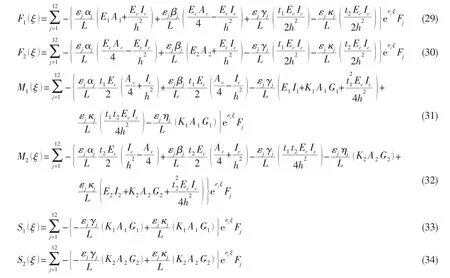
2 夹层梁动态刚度矩阵

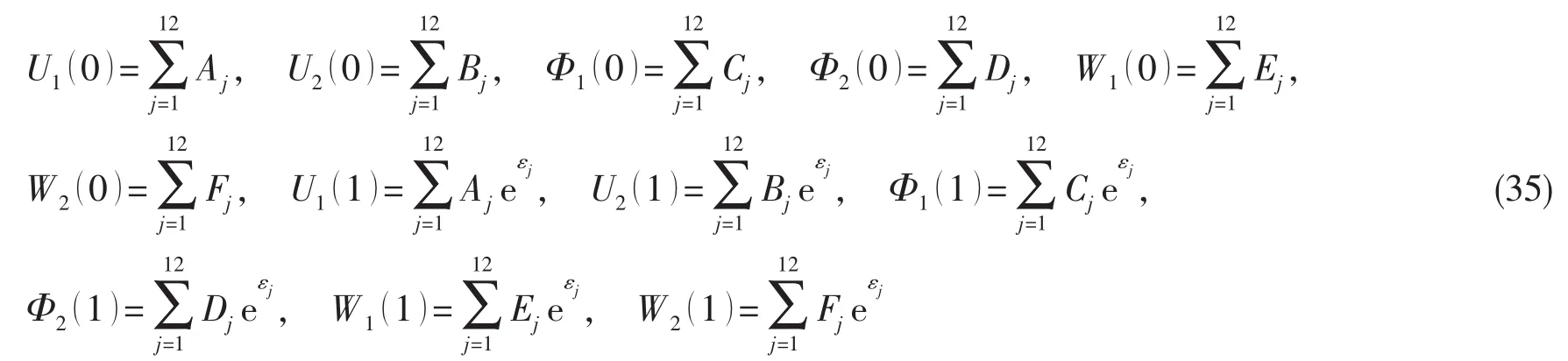
将（27）式代入上式，并写成矩阵形式：

或者写作：

或者写作：

其中矩阵元素tij具体表示如下：

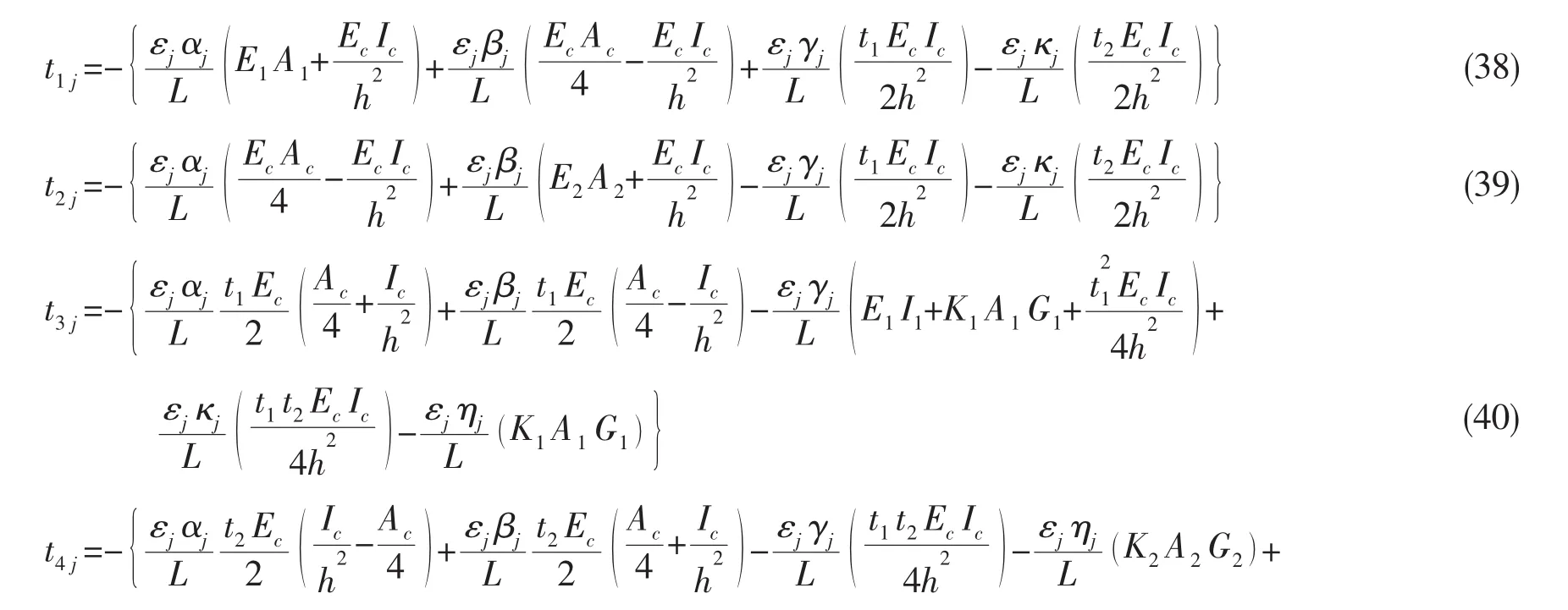
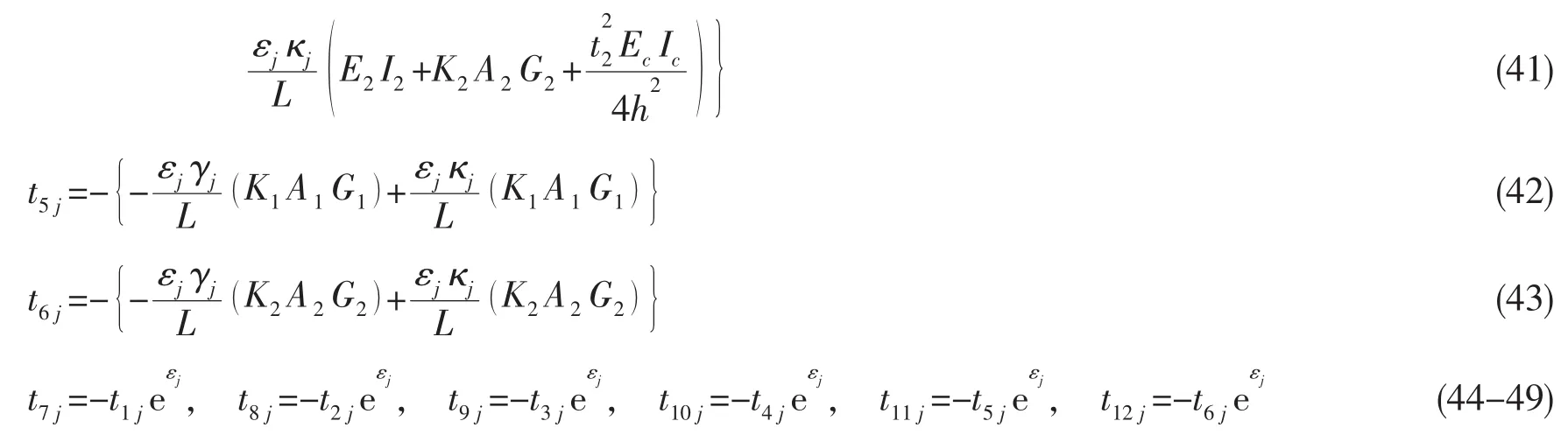
这里 j=1，…12。

联合（36）式和（37）式可得：

其中矩阵K=TH-1，即为所求夹层梁的动态刚度矩阵。

假设一三层均为各向同性的均匀夹层梁结构，长为L，宽为b；上下面层的厚度为ti，质量密度为ρi，弹性模量为Ei，惯性矩为Ii；芯层的厚度为h，密度为ρc，弹性模量为Ec，惯性矩为Ic。 其中i=1，2，分别表示上下面层，下文同。

3 数值计算

算例1 为验证本文推导正确效性，取文献[4]中所给算例进行计算比较：各层横截面为矩形均匀梁的夹层梁，L=500 mm，b=40 mm，t1=15 mm，t2=tc=20 mm。文中所用到的钢材质和橡胶材质的物理参数如下：Es=210 GPa，Gs=80 GPa，ρs=7 850 kg/m3，Er=1.5 MPa，Gr=0.5 MPa，ρr=950 kg/m3。 其中下角标 s表示钢材质，下角标r表示橡胶材质。剪切修正系数取2/3。梁一端刚固一端自由。

算例2 算例1中梁模型几何特性及边界条件不变，但采用石墨芯层，物理量为（用下标l表示）：El=16 GPa，Gl=5.5 GPa，ρl=11 100 kg/m3。

应用动态刚度矩阵法分别计算两算例梁模型固有频率。取前四阶固有频率结果进行比较分析，如表1所示。从表1中可以看出，本文算例1计算结果低于文献[4]计算结果，这是因为在本文的动态刚度矩阵推导过程中，考虑了夹层梁芯层的垂向压缩变形的影响，当芯层较软，即模量与面梁相比很小的情况下，这种影响是不可忽略的。而本文算例2计算结果与文献[4]结果吻合较好，这是因为算例2中的芯层弹性模量与面梁弹性模量相差不大，且芯层密度大，所以芯层的垂向压缩变形影响不大。

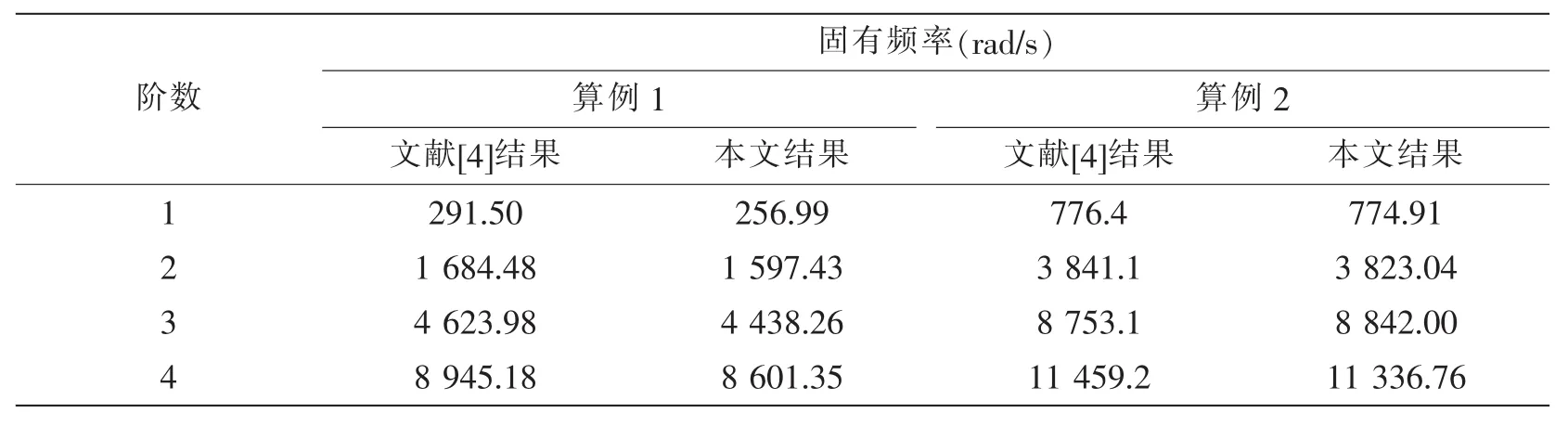
表1 悬臂夹层梁前四阶固有频率Tab.1 Natural frquencies of sandwich beams with cantilever end conditions

算例3为说明在推导夹层梁动态刚度矩阵中考虑芯层垂向压缩变形的合理性，分别计算考虑及不考虑芯层垂向压缩变形的夹层梁的固有频率。本算例取自ABAQUS的考题集。悬臂梁几何及物理参数：L=1 000 mm，b=100 mm；t1=t2=4 mm，Ei=1.0×107N/cm2；芯层厚度 tc=50 mm，Gc=1.0×104N/cm2。 在ABAQUS考题集中只给定了芯层的泊松比及剪切模量，忽略了其它物理参数。此算例中本文主要反映芯层的垂向压缩变形，因此根据各向同性材料杨氏模量与剪切模量间的计算关系，取Ec=2.0×104N/cm2。本文不考虑芯层垂向压缩模型是假定夹层梁面层和芯层具有相同的挠度，并略去芯层垂向应变和应力的相关项。计算结果见表2。

表2 悬臂夹层梁高阶固有频率Tab.2 Natural frquencies of sandwich beams with cantilever end conditions

从结果表2中可以看出，本文考虑可压缩解与不考虑可压缩解在前40阶吻合较好，但是在第42阶考虑可压缩解与不考虑可压缩解相差12 Hz。可见悬臂梁在第42阶产生了对称的弯曲变形，即芯层产生了垂向压缩变形，而不考虑垂向可压缩变形模型则未显示这一变形结果，导致两种结果相差较大。由于动态刚度矩阵一般用于结构的高频振动研究，因此在推导夹层梁的动态刚度矩阵时考虑芯层垂向可压缩变形的影响是至关重要的。

4 结 论

本文在考虑夹层梁芯层垂向压缩变形影响的夹层梁位移模式基础上，推导了考虑芯层垂向压缩变形影响的夹层梁动态刚度矩阵。利用所得动态刚度矩阵分别计算了以橡胶和石墨为芯层材料的悬臂夹层梁的前四阶固有频率，所得结果与文献结果相比较，证明本文方法是正确可靠的；利用经典算例分别计算其考虑及不考虑芯层垂向压缩变形的模型高阶固有频率，结果对比表明在夹层梁动态刚度矩阵推导和高频计算中考虑芯层垂向压缩变形是合理的。

[1]Banerjee J R.Free vibration of sandwich beams using the dynamic stiffness method[J].Computers and Structures,2003,81(1):1915-1922.

[2]Banerjee J R,Sobey A J.Dynamic stiffness formulation and free vibration analysis of a three layered sandwich beam[J].International Journal of Solids and Structures,2005,42(23):2181-2197.

[3]Howson W P,Zare A.Exact dynamic stiffness matrix for flexural vibration of three-layered sandwich beams[J].Journal of Sound and Vibration,2005,282(5):753-767.

[4]Banerjee J R,Cheung C W,Morishima R,et al.Free vibration of a three-layered sandwich beam using the dynamic stiffness method and experiment[J].International Journal of Solids and Structures,2007,44(12):7543-7563.

[5]Banerjee J R,Sua H,Jayatunga C.A dynamic stiffness element for free vibration analysis of composite beams and its application to aircraft wings[J].Computersamp;Structures,2008,86(18):573-579.

[6]Jun L,Hongxing H.Dynamic stiffness analysis of laminated composite beams using trigonometric shear deformation theory,Compos Struct(2008),doi:10.1016/j.compstruct.2008.09.002.

[7]Boscolo M,Banerjee J R.Dynamic stiffness formulation for composite Mindlin plates for exact modal analysis of structures.Part I:Theory[J].Computersamp;Structures,2012,96-97:61-73.

[8]Boscolo M,Banerjee J R.Dynamic stiffness formulation for composite Mindlin plates for exact modal analysis of structures.Part II:Results and applications[J].Computersamp;Structures,2012,96-97:74-83.

[9]王海英,赵德有.芯板横向可压缩位移模式的夹层板结构动力有限元分析[J].船舶力学,2009,13(3):795-805.Wang Haiying,Zhao Deyou.Finite element analysis for sandwich plates with moderately thick viscoelastic cores[J].Journal of Ship Mechanics,2009,13(3):795-805.

Exact dynamic stiffness matrix of sandwich beams with vertically compressed core

WANG Hai-ying1,ZHANG Gui-yong2
(1.Navigation and Naval Architecture College,Dalian Ocean University,Dalian 116023,China;2.School of Naval Architecture Engineering,Dalian University of Technology,Dalian 116024,China)

An accurate dynamic stiffness matrix for a sandwich beam with vertically compressed core is developed and subsequently used to investigate its free vibration characteristics.Each face layer of the beam is idealized by the Timoshenko beam theory.Linear variation of displacements through the thickness of the core is assumed,so that the transverse normal deformation is taken into account.The combined system is reduced to a twelfth-order system using symbolic computation.An exact dynamic stiffness matrix is then developed by relating amplitudes of harmonically varying loads to those of the responses.The resulting dynamic stiffness matrix is used with particular reference to the Wittrick-Williams algorithm to carry out the free vibration analysis of a few illustrative examples.

dynamic stiffness matrix;sandwich beam;natural frequency

O327

A

10.3969/j.issn.1007-7294.2017.11.008

1007-7294（2017）11-1383-10

2017-04-01

国家自然科学基金项目（51579042）

王海英（1980－），女，讲师，E-mail：wanghaiying@dlou.edu.cn；

张桂勇（1978－），男，教授，博士生导师。