多浮体铰接薄板结构运动响应研究

王 科，张志强，刘 影

（大连理工大学 工业装备结构分析国家重点实验室 工程力学系，辽宁大连116024）

多浮体铰接薄板结构运动响应研究

王 科，张志强，刘 影

（大连理工大学 工业装备结构分析国家重点实验室 工程力学系，辽宁大连116024）

应用Newman的广义运动模态分解方法和拉格朗日乘子法，基于波浪辐射和绕射理论建立了铰接多浮体结构水动力响应的运动方程，应用预修正快速傅里叶变换（pFFT）的边界元方法对由15块板组成的铰接多浮体结构的运动响应进行了研究。数值结果表明该pFFT方法计算精度和计算速度均很高，可用于任意形状和约束状态的多体结构的水动力分析。板间距的改变对铰接点处垂荡和横摇影响较大。

预修正快速傅里叶变换（pFFT）方法；波浪辐射和绕射；铰接多浮体结构；垂荡和横摇

0 引 言

早期关于多浮体水动力方面的研究方法主要有特征值展开法[1]，多体绕射法[2]和边界元方法[3]，上述研究由于当时计算条件有限，划分的单元数量不大，物体形状也都很简单，而且考虑物体之间的相互作用时仅仅是将各自独立运动的辐射势简单叠加，并不是真正意义上的相互影响运动。

真正解决多浮体相互影响运动的理论是由Newman[4]提出的广义运动模态理论。这种广义模态包含了多浮体的所有刚体模态，各种连接模态，弹性模态等。利用该方法，Leeamp;Newman[5]对铰接5方箱系统水弹性问题展开了研究，讨论了浮体刚度对结构运动响应以及铰链剪切应力的影响。Sun，EatockTaylor和Choo[6]通过拉格朗日乘子法推导出铰接多浮体系统的约束矩阵，并建立了铰接多浮体系统的运动方程。滕斌，何广华，李博宁等[7]通过比例边界有限元方法分别对两方箱以及三方箱结构的波浪绕射问题进行了研究。谢楠和郜焕秋[8]利用三维源汇分布法对波浪中自由漂浮的两浮体水动力相互作用问题进行了研究。吴广怀，沈庆，陈徐均等[9]利用格林函数法对两浮体以及三浮体在波浪作用下的水动力系数问题进行了研究，分析了浮体—方箱系统以及双方箱系统中两浮体相互作用的附加质量、阻尼系数。史琪琪，柏木正，杨建民等[11]采用高阶边界元方法和波浪交互理论研究了波浪交互理论在求解三维多浮体水动力问题中的适用性。吴必军，胡城，郑永红等[12]通过匹配特征函数展开法对双圆柱的波浪绕射和辐射问题进行了研究。

在以上关于单浮体以及多浮体系统水动力问题研究中，浮体个数大多为两浮体或三浮体，所研究的结构形式主要有圆柱，方箱和船舶等等，采用的方法都是传统边界元方法。当浮体单元数目较多的时候，离散单元数目将会变得非常巨大，传统边界元方法不再适用。针对这一问题，广大学者们相继发展了多种快速算法，以便降低存储需求和计算复杂度，并且都致力于加快迭代求解过程中矩阵向量积的计算。预修正快速傅里叶变换方法（pFFT）不改变格林函数的具体形式，可以用于任意格林函数问题的求解。因此在波浪与结构物相互作用的水动力问题计算中，pFFT方法更加方便和灵活。

本文以由15块板组成的铰接多浮体结构作为研究对象，利用预修正傅里叶变换（pFFT）方法对其在不同波浪作用下的运动响应进行研究。研究模型中薄板的长宽比较大，超强的几何奇异性要求算法必须具有很高的计算精度。数值实验表明本研究采用的pFFT方法对格林函数基本解含波动项的问题完全适用，计算精度高且计算速度快。文章第一章介绍了本研究所采用的数学模型和运动响应的计算方法，第二章为铰接15薄板结构运动响应结果分析，第三章为结论与建议。

1 数学模型及基本公式

1.1 控制方程及边界条件

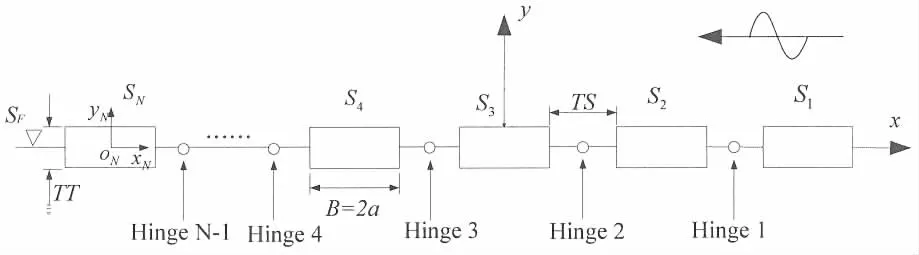
图1 多浮体计算模型Fig.1 Calculation sketch of multiple plates

计算模型如图1所示，假定波浪中有N个做微幅简谐振荡运动的刚性浮体，空间固定的整体坐标系oxy原点位于无扰动的自由水面，x轴水平向右为正，y轴垂直向上为正。入射波浪沿x轴负向向左传播。局部坐标系o1x1y1，o2x2y2，…，oNxNyN的原点位于各浮体重心处，且随浮体一起运动。为结构湿表面，其中S1，S2，…，SN为各浮体湿表面，物面法线方向以指向流体内部为正。

1.2 速度势的分解

假定浮体做微幅简谐振荡运动，基于线性势流理论，流场内速度势可表示为：

其中：Re｛｝表示取复数表达式的实部，ω为波浪圆频率，t为时间，φ为与时间无关的空间复速度势，满足拉普拉斯方程。

依据运动线性叠加原理，空间复速度势φ可以分解为入射势φI、绕射势φD和辐射势φR之和：

波浪入射势φI可表达为如下形式：

其中：K=ω2/g为波数，A0为波浪振幅。

对于流场中有N个浮体的多体问题[4]，辐射势可以分解为如下形式：

其它浮体均固定不动时的单位速度辐射势。辐射势φj满足的物面边界条件为：

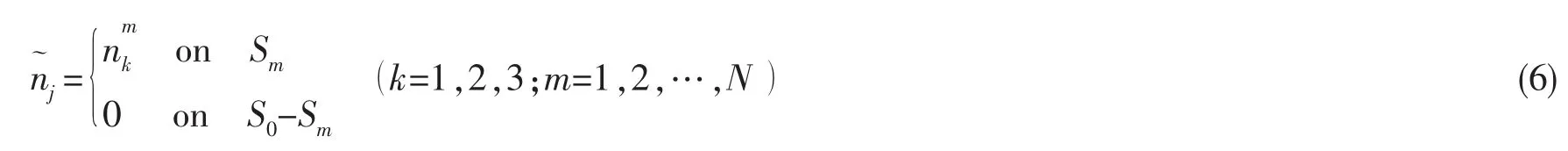
辐射势φj定解问题的数学形式为：

其中：R为流场中某点离扰动源的距离，K为波数。

绕射势φD也满足方程（7）的控制方程，其满足的物面边界条件为：

1.3 边界积分方程的建立

应用格林定理，可得求解φj和φD的边界积分方程如下：

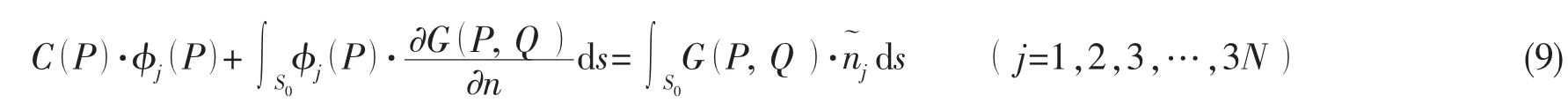
定义散射势 φS=φI+φD：

本文采用新的边界积分方程直接求解φS：

其中：

1.4 结构所受波浪力

求解出浮体的散射势和辐射势以后，即可得到任意浮体m所受波浪力为：

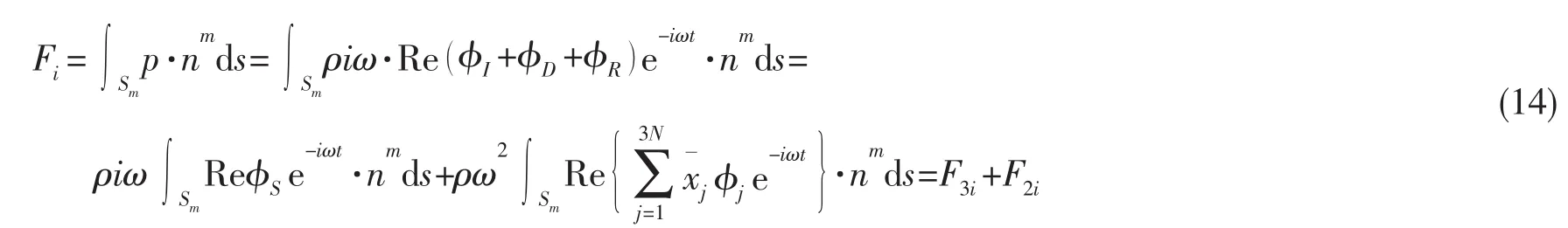
其中：F3i为散射波浪力，F2i为辐射波浪力。（14）式中对任意浮体m定义水动力系数为：

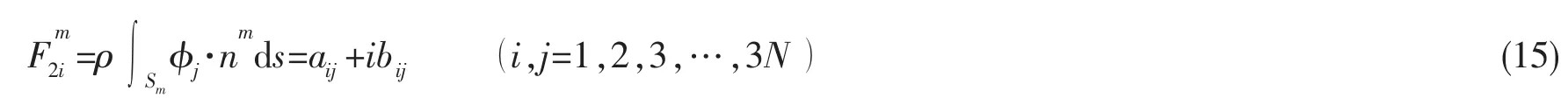
其中：aij为附加质量系数，bij为阻尼系数。

1.5 边界积分方程的离散及pFFT求解

将物面边界S0离散为一系列微小单元，并假定各物理量在单元上呈线性分布。最终可将积分方程离散为如下形式：

式中：nb为物面节点个数。

对于多浮体的大规模边界元计算问题，（16）式可通过预修正傅里叶变换方法[13-14]（pFFT）转换成下式进行快速求解：

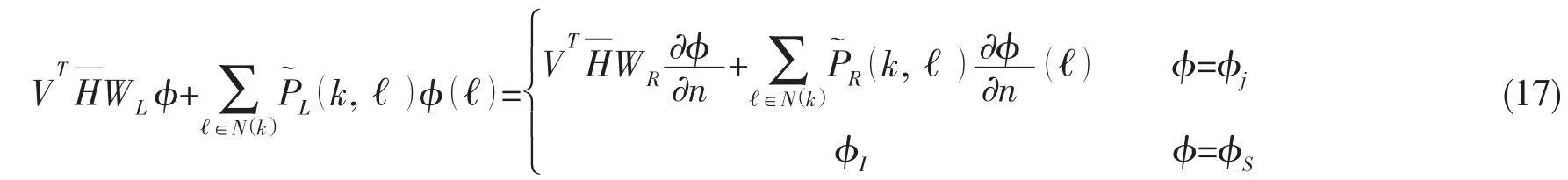
采用线性元进行离散时，pFFT的近场积分具有以下形式：

公式（18）中包含log r1和log r2项的系数可采用线性解析方法求得，IC项为正则项，其积分不含奇异性，可通过数值积分来计算。

本文通过线性单元对结构表面进行离散，并通过形心坐标来判断物面单元与pFFT子正方形之间的从属关系，能够方便处理一个面元横跨两个子正方形的情形。另外，由于本文所采用的格林函数的特殊性，若子正方形k及其临近子正方形l都位于自由水面上，则需要对log r1、log r2以及IC项都进行预修正，而其它情况只需要对log r进行预修正。

1.6 铰接多浮体系统运动方程的建立

N个浮体的运动方程如下[6]：

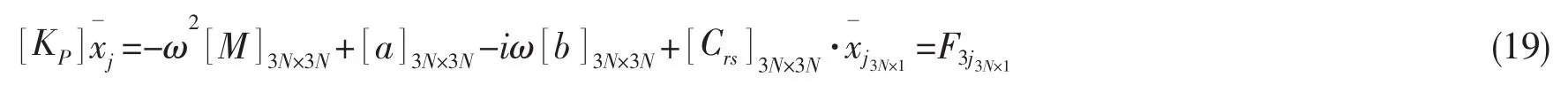
假设浮体间采用刚性铰接，则与铰接点相连的两浮体只有相对转动，而没有相对平移，连接点处应满足位移连续性条件。约束方程可表示为：

根据（19）式和（20）式，应用拉格朗日乘子法，可得：

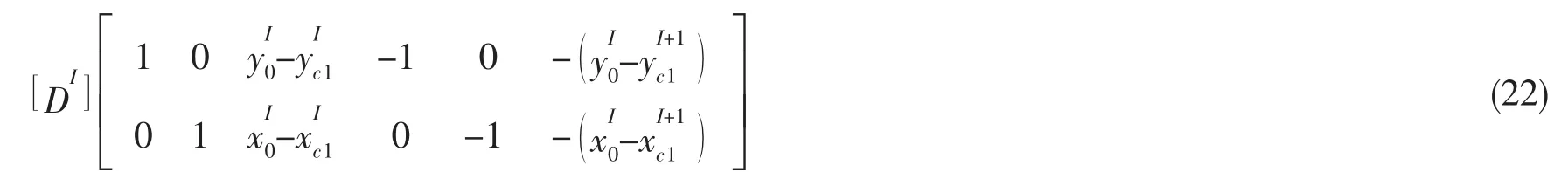
2 铰接多薄板结构水动力分析

2.1 铰接15浮板水动力分析

计算模型如图1所示。15块尺寸相同的薄板相互铰接，浮于自由水面。x轴水平向右为正，y轴垂直向上为正，入射波浪从右向左传播。单板长度B=0.4 m，板厚TT=0.005 m，入射波浪波高为0.01 m，考虑不同板间距TS对结构铰接点处运动振幅的影响。

图2-7为迎浪端铰接点1，2，3在不同间距下垂荡和横摇振幅计算结果。通过结果可以看出，在长波作用下，各铰接点垂荡振幅为1，横摇振幅为0。随着相对板长KB/2的增加，垂荡和横摇结果曲线均呈先增加，之后振荡增加的趋势。相对板长KB/2较大时，波浪频率的改变对铰接点垂荡和横摇运动幅值影响较大，结果曲线变化剧烈。

当0＜KB/2＜0.8时，增加板间距会令各铰接点垂荡和横摇振幅增加。在0.8＜KB/2＜1.2范围内垂荡和横摇振幅对板间距的改变较为敏感。对于铰接点1而言，其最大垂荡振幅为2.6，最大横摇振幅为1.7，最大振幅对应板间距TS=0.15 m，相对板长KB/2=1.15；对于铰接点2而言，其最大垂荡振幅为2.45，最大横摇振幅为1.58，最大振幅对应板间距TS=0.2 m，相对板长KB/2=1.1；对于铰接点3而言，其最大垂荡振幅为2.88，最大横摇振幅为1.95；最大振幅对应板间距TS=0.2 m，相对板长KB/2=1.1。

铰接点处的垂荡和横摇运动是由与其相邻的两块薄板的垂荡和横摇运动共同决定的，板的垂荡运动和横摇运动在铰接点处引起的位移可能互相叠加，也可能互相抵消。该特性会导致在相同波浪入射时，且较小间距情况下铰接点运动振幅比间距较大情况下铰接点运动振幅大的情况。例如对于铰接点1，当KB/2=1.0时，间距TS=0.15 m的垂荡和横摇振幅要比TS=0.2 m的垂荡和横摇振幅大。

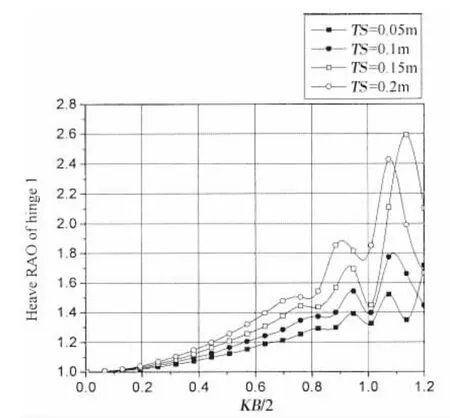
图2 铰接15浮板不同间距时铰接点1垂荡RAOFig.2 Heave RAO at hinge 1 with different TS

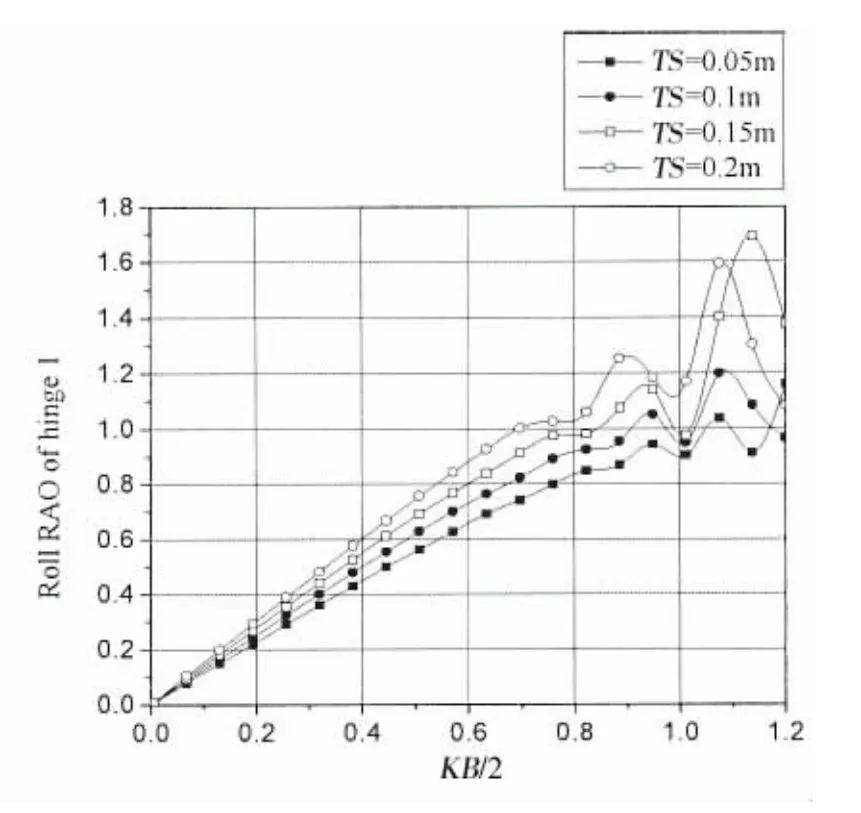
图3 铰接15浮板不同间距时铰接点1横摇RAOFig.3 Roll RAO at hinge 1 with different TS

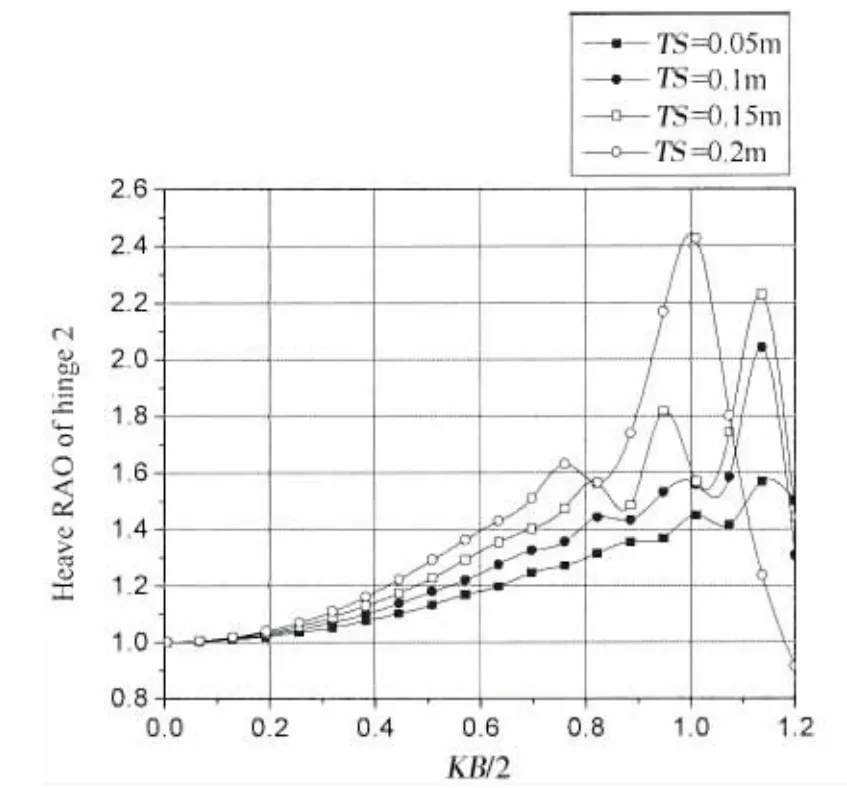
图4 铰接15浮板不同间距时铰接点2垂荡RAOFig.4 Heave RAO at hinge 13 with different TS

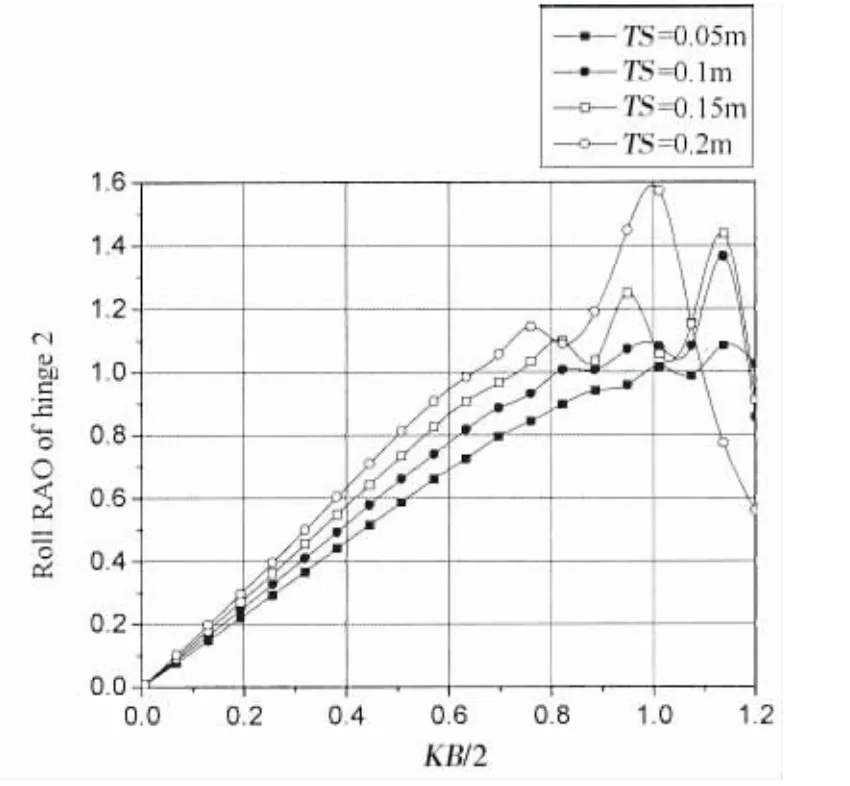
图5 铰接15浮板不同间距时铰接点2横摇RAOFig.5 Roll RAO at hinge 2 with different TS

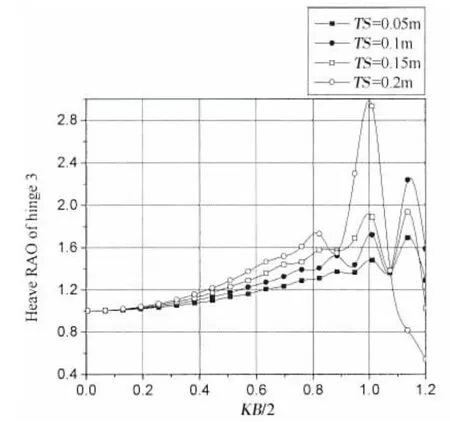
图6 铰接15浮板不同间距时铰接点3垂荡RAOFig.6 Heave RAO at hinge 3 with different TS

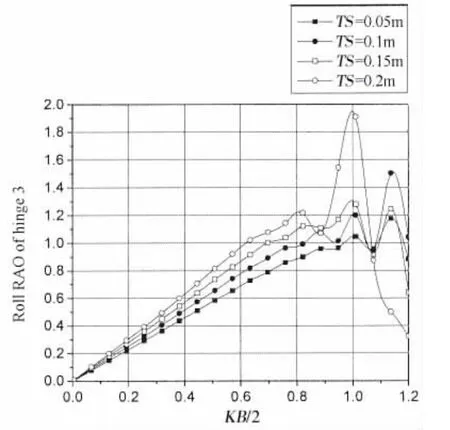
图7 铰接15浮板不同间距时铰接点3横摇RAOFig.7 Roll RAO at hinge 3 with different TS

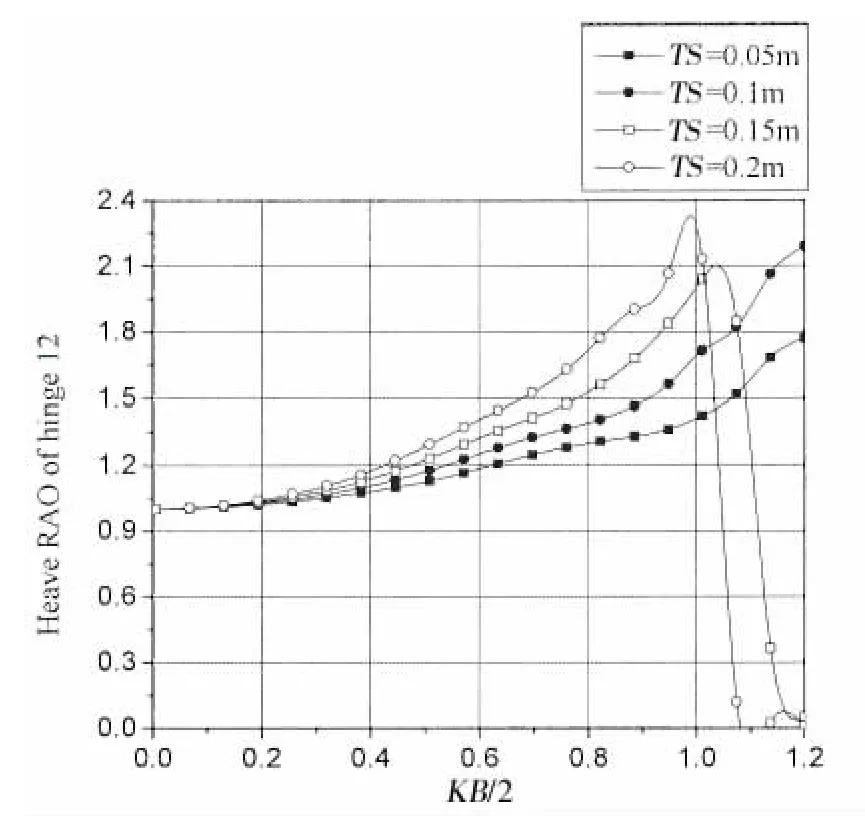
图8 铰接15浮板不同间距时铰接点12垂荡RAO Fig.8 Heave RAO at hinge 12 with different TS

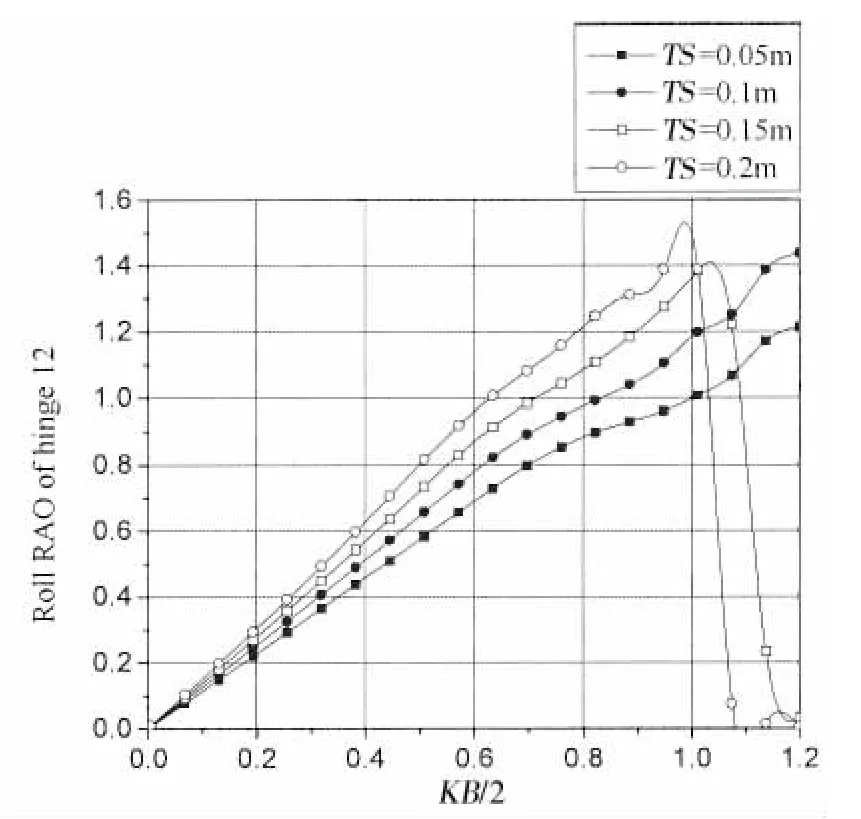
图9 铰接15浮板不同间距时铰接点12横摇RAOFig.9 Roll RAO at hinge 12 with different TS

图10 铰接15浮板不同间距时铰接点13垂荡RAOFig.10 Heave RAO at hinge 13 with different TS

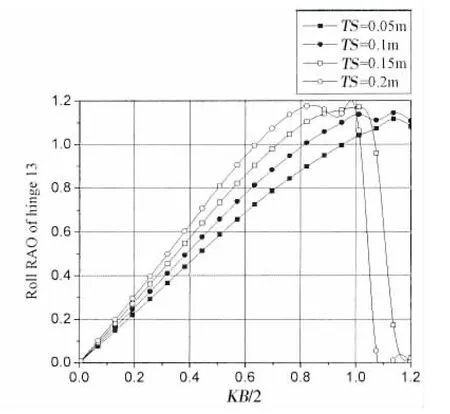
图11 铰接15浮板不同间距时铰接点13横摇RAOFig.11 Roll RAO at hinge 13 with different TS

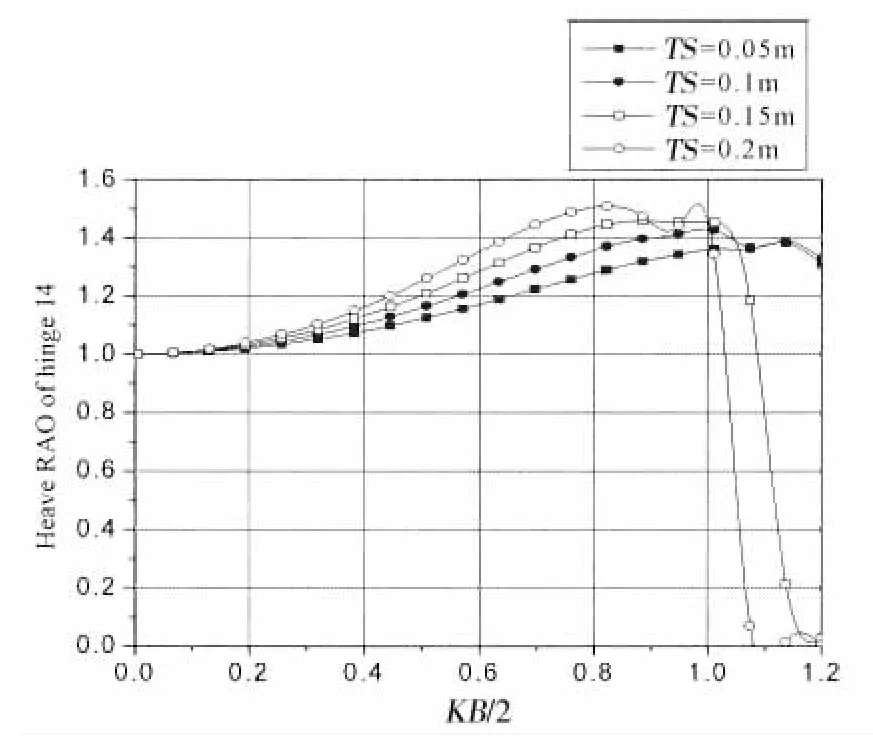
图12 铰接15浮板不同间距时铰接点14垂荡RAOFig.12 Heave RAO at hinge 14 with different TS

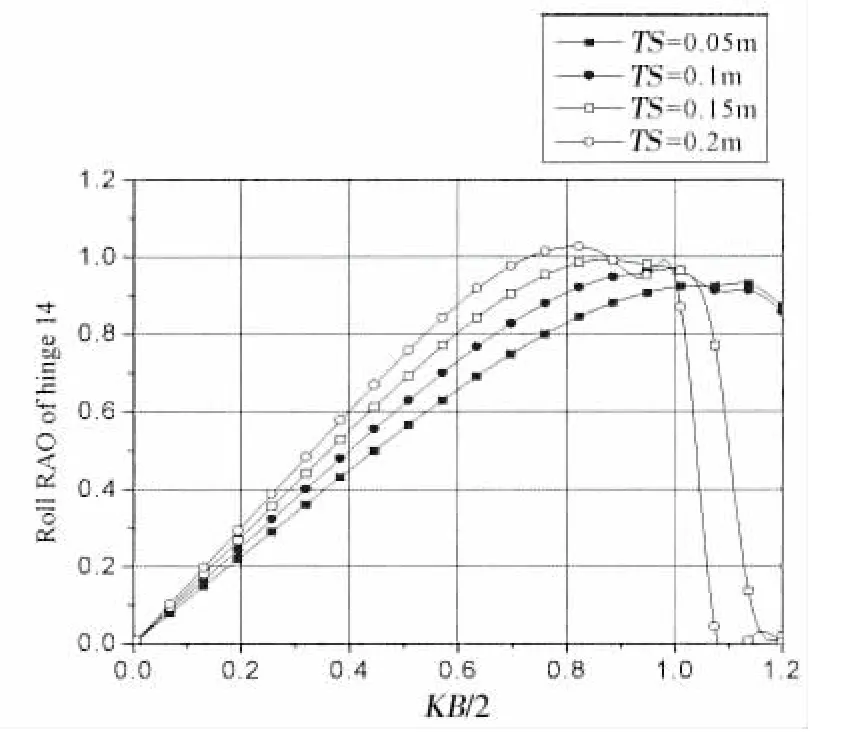
图13 铰接15浮板不同间距时铰接点14横摇RAOFig.13 Roll RAO at hinge 14 with different TS

图8-13为背浪端铰接点12，13，14在不同间距下垂荡和横摇振幅结果。通过结果可以看出，在整个计算范围内，随着相对板长KB/2的增加，铰接点垂荡和横摇都呈先增加后减小的趋势。在0.4＜KB/2＜1.0范围内，增加板间距可令各铰接点垂荡和横摇振幅增大。与迎浪端铰接点相比，处于背浪端的铰接点垂荡和横摇振幅的最大值比迎浪端小。铰接点12最大垂荡振幅为2.3，最大横摇振幅为1.55，对应板间距TS=0.2 m，KB/2=0.98；铰接点13最大垂荡振幅为1.85，最大横摇振幅为1.2，对应板间距TS=0.2 m，KB/2=0.95；铰接点14最大垂荡振幅为1.5，最大横摇振幅为1.05，对应板间距TS=0.2 m，KB/2=0.83。另外在某些波浪频率下，背浪端铰接点的垂荡和横摇振幅出现0值。这是因为此时板的垂荡和横摇运动在铰接点处相互抵消。因此，铰接点处RAO为0，并不一定代表板不动。

当间距TS=0.1 m时，铰接15薄板的迎浪端铰接点1处最大垂荡振幅为1.8，最大横摇振幅为1.2，对应相对板长KB/2=1.05。对比TS=0.1 m时铰接6薄板结果可以发现，当板的个数增加时，结构迎浪端铰接点的最大运动振幅减小。在结构设计过程中，可通过增加板的个数来达到减小铰接点处最大运动振幅的目的。无论铰接6薄板还是铰接15薄板，铰接点处最大垂荡和横摇振幅都出现在KB/2较大的情况。因此铰接多板结构应避免在KB/2较大的情况下使用。

3 结 论

本文应用预修正快速傅里叶变换方法对铰接15薄板的水动力问题进行了分析，研究发现：

（1）在长波作用下，各铰接点垂荡振幅为1，横摇振幅为0。随着相对板长 的增加，垂荡和横摇振幅均呈先增加后减小的趋势。

（2）对于铰接15薄板结构而言，当间距TS=0.1 m时铰接点1处最大垂荡振幅为1.8，最大横摇振幅为1.2，对应相对板长KB/2=1.05。增加铰接板的个数可以减小各铰接点最大垂荡和最大横摇振幅。

（3）对于铰接多浮体薄板结构，铰接点处的运动受其相邻的薄板垂荡和横摇运动共同影响。通常情况下板间距越大，铰接点处垂荡和横摇运动振幅越大。但是由于板的垂荡和横摇运动在铰接点处可能叠加也可能抵消，较小间距时铰接点运动幅度可能会比间距较大时铰接点的运动幅度大。

[1]Ohkusu M.On the heaving motion of two circular cylinders on the surface of a fluid[R].Reports of Research Institute for Applied Mechanics,XVII,No.58,1969:167-185..

[2]Kagemoto H,Yue D K P.Interactions among multiple three dimensional bodies in water waves:an exact algebraic method[J].J Fluid Mech.,166,1986:189-209.

[3]van Oortmerssen G.Hydrodynamic interaction between two structures,floating in waves[C]//Proc.2nd Intl.Conf.on Behaviour of Offshore Structures(BOSS’79).London,1979:339-356.

[4]Newman J N.Wave effects on deformable bodies[J].Applied Ocean Research,1994,16(1):47-59.

[5]Lee C H,Newman J N.An assessment of hydroelasticity for very large hinged vessels[J].Journal of Fluids and Structures,2000,14(7):957-970.

[6]Sun L,Eatock Taylor R,Choo Y S.Responses of interconnected floating bodies[J].Ies Journal Part A Civilamp;Structural Engineering,2011,4(3):143-156.

[7]何广华,滕 斌,李博宁,等.应用比例边界有限元法研究波浪与带狭缝三箱作用的共振现象[J].水动力学研究与进展(A辑),2006,21(3):418-424.He Guanghua,Teng Bin,Li Boning,et al.Research on the hydrodynamic influencefrom the gaps between three identical boxes by a scaledboundary finite elementmethod[J].Journal of Hydrodynamics(A),2006,21(3):418-424.

[8]谢 楠,郜焕秋.波浪中两个浮体水动力相互作用的数值计算[J].船舶力学,1999(2):7-15.Xie Nan,Gao Huanqiu.Numerical calculation of hydrodynamic interaction of two bodies floating in waves[J].Journal of Ship Mechanics,1999(2):7-15.

[9]吴广怀,沈 庆,陈徐均,等.浮体间距对多浮体系统水动力系数的影响[J].海洋工程,2003(4):29-34.Wu Guanghuai,Shen Qing,Chen Xujun,et al.Influence of the distance between floating bodies on hydrodynamic coefficients of floating multi-body system[J].The Ocean Engineering,2003(4):29-34.

[10]朱仁传,朱海荣,缪国平.具有小间隙的多浮体系统水动力共振现象[J].上海交通大学学报,2008(8):1238-1242.Zhu Renchuan,Zhu Hairong,Miao Guoping.Influences on hydrodynamics of multiple floating structures with small gap in between[J].Journal of Shanghai Jiaotong University,2008(8):1238-1242.

[11]史琪琪,柏木正,杨建民,等.基于高阶边界元法和波浪交互理论的三维相邻多浮体问题研究[J].船舶力学,2012(5):504-513.Shi Qiqi,Masashi Kashiwagi,Yang Jianmin,et al.Research on 3-D problem of adjacent multiple floating bodies based on HOBEM and wave interaction theory[J].Journal of Ship Mechanics,2012(5):504-513.

[12]吴必军,胡 城,郑永红,等.双浮体自由垂向振荡响应特性[J].水动力学研究与进展A辑,2006,21(4):458-464.Wu Bijun,Hu Cheng,Heng Yonghong,et al.Heaving-motion response of two freely floating vertical cylinders[J].Journal of Hydrodynamics(A),2006,21(4):458-464.

[13]Korsmeyer T,Klemas T,White J,et al.Fast hydrodynamic analysis of large offshore structures[C]//The Ninth International Offshore and Polar Engineering Conference.Brest,France,1999.

[14]Jiang SC,Teng B,Gou Y,Ning D Z.A precorrected-FFT higher-order boundary element method for wave-body problems[J].Eng Anal Bound Elem,2012,36:404-415.

Study on motion response of floating hinged multi-plates

WANG Ke,ZHANG Zhi-qiang,LIU Ying
(State Key Laboratory of Structural Analysis for Industrial Equipment,Department of Engineering Mechanics,Dalian University of Technology,Dalian 116024,China)

Based on wave radiation and diffraction theory,the motion equations of hinged multi-bodies are established according to the Lagrangian multiplier method and the generalized mode expansion method proposed by Newman.The precorrected Fast Fourier Transform(pFFT)method is utilized to analyze the hydrodynamics of multi-bodies that consists of horizontal,rigid,thin plates with hinged connection.The RAOs of motion are discussed.Numerical results show that pFFT method is very accurate and can be used in the hydrodynamic analysis of complex multi-bodies with arbitrary shape and constraints.The changing of interval space between plates is critical for heave and roll of hinged points.

precorrected Fast Fourier Transform(pFFT)method;wave radiation and diffraction;multi-bodies;RAOs of motion;heave and roll

U661.4

A

10.3969/j.issn.1007-7294.2017.11.006

1007-7294（2017）11-1365-09

2017-08-20

国家自然科学基金项目（51379037）；国家重点基础研究发展计划资助（2013CB036101）

王 科（1970-），男，副教授，E-mail：kwang@dlut.edu.cn；

张志强（1984-），男，博士研究生。