自由来流角度影响下壁面湍流脉动压力波数—频率谱的大涡模拟计算分析研究

张晓龙，张 楠，吴宝山

（中国船舶科学研究中心 水动力学重点实验室，江苏 无锡214082）

自由来流角度影响下壁面湍流脉动压力波数—频率谱的大涡模拟计算分析研究

张晓龙，张 楠，吴宝山

（中国船舶科学研究中心 水动力学重点实验室，江苏 无锡214082）

壁面湍流脉动压力是重要的流噪声声源，对壁面湍流脉动压力及其波数—频率谱进行数值计算是流声耦合领域的重要课题。文章在已有工作的基础上，采用大涡模拟方法（LES）结合动态亚格子涡模型（DSL）与千万量级的精细网格，对不同自由来流角度影响下壁面湍流脉动压力及其波数—频率谱进行了数值计算与分析。首先，介绍了大涡模拟基本方法，包括：大涡模拟的物理内涵、基本方程以及所采用亚格子涡模型的表达式。其次，介绍了湍流脉动压力波数—频率谱及其计算与分析方法。再次，对不同自由来流角度情况下的湍流脉动压力及其波数—频率谱进行了计算，并将计算结果进行了比较分析，深入讨论了自由来流角度对湍流脉动压力及其波数—频率谱的影响。结果表明，在自由来流角度影响下，湍流脉动压力及其波数—频率谱主要参数（包括波数—频率谱的谱级峰值、迁移脊在波数—频率域内的分布范围、迁移速度和无量纲迁移速度等）均发生了明显变化，说明自由来流角度对湍流脉动压力波数—频率谱有显著影响，且边界层内湍流脉动压力的能量主要沿流向分布。因此，为了更加准确可靠地研究边界层内湍流脉动压力的主要统计特性及其波数—频率谱，传感器阵列或监测点阵列布置方向应与当地流向（局部剪应力线或摩擦力线）一致。

湍流脉动压力；波数—频率谱；自由来流角度影响；大涡模拟

0 引 言

壁面湍流脉动压力是湍流非定常特性的重要表征，同时也是流激噪声的重要来源，因此，其在流体诱发振动与噪声的许多工程应用问题中都备受关注。

目前，湍流脉动压力及其波数—频率谱的研究主要还是基于试验测量，通过对湍流脉动压力测量数据进行处理和分析，达到对脉动压力定性与定量分析的目的。其研究关注重点是脉动压力的谱型、幅值及变化规律，特别是关注湍流脉动压力波数—频率谱的特性。人们研究湍流脉动压力及其波数—频率谱的目的主要在于了解湍流结构的时空关联特性以及为流激结构振动声辐射提供输入。

就湍流脉动压力的分析方法而言，自上世纪中叶Corcos[1-2]基于Fourier变换得到最早的波数—频率谱模型以来，湍流脉动压力主要分析手段一直都是基于Fourier变换，在频域和波数域内，对脉动压力的时空关联特性、多尺度特性等进行分析研究。Fourier变换物理概念清晰，简便易行，数据直观，便于理解，加深了我们对湍流脉动压力以及湍流现象的深入理解，现在仍是研究湍流脉动压力的主要分析手段。

简言之，目前对于湍流脉动压力，尤其是其波数—频率谱的大量研究主要是以试验测量和Fourier分析为主要手段。

Abraham和Keith（1998）[3]在消音水洞中，通过在流向等间距布置48个传感器，测得了壁面湍流脉动压力流向的波数—频率谱，其使用的传感器阵列具有较高的分辨率，从而保证了波数—频率谱“迁移脊”和部分低波数区域的测量准确度。用基于试验测得的参数得到的时空尺度对波数—频率谱进行了归一化处理，比较了不同归一化处理方式的效果。

Cipolla和Keith（2000）[4]在前人工作的基础上，研究了逆压梯度和顺压梯度对湍流脉动压力自功率谱及波数—频率谱的影响，结果表明采用外部变量可以使频谱在窄带频域内汇聚。但由于测试数据的限制，难于对频谱低波数区域展开更深入研究。

Cipolla和Keith（2008）[5]在庞多雷湖（Lake Pend Oreille）中进行圆柱表面拖曳阵上的湍流脉动压力测试，试验在实尺度模型上进行，速度范围为10-18节，并得到了相应的波数—频率谱、自功率谱和迁移速度等。试验结果表明当直拖时，波数—频率谱中有明显的迁移脊；当回转时，流体诱发的振动会主要影响波数-频率谱的低频部分，高频部分则更快地衰减。在分析测试数据时Cipolla和Keith仍然引用Abraham（1998）的试验结果来证实其测试结果的合理性，这也足见Abraham（1998）的测量结果得到业界认可，具有经典价值，对湍流脉动压力测量与波数—频率谱的分析均产生了重要影响。

Bonness等人（2010）[6]基于湍流脉动压力激发的圆柱管道振动数据，对低波数区域充分发展的管道湍流边界层脉动压力进行了测量，并基于试验测量结果对几种常用波数—频率谱模型进行了比较分析。结果表明，Corcos模型预报结果偏大，波数—频率谱测量值介于Smol’yakov模型和Chase模型之间。

此外，随着数值模拟方法的逐渐成熟和计算水平的提高，人们也开始对湍流脉动压力进行数值模拟计算研究。

Manoha等人（2000）[7]采用大涡模拟方法，对厚平板钝后缘的非稳态流场的脉动压力进行了计算，并对尾缘壁面脉动压力进行了分析，其幅值、频率以及流向的演化均与钝后缘翼型的测量结果吻合很好。

Wang等（2009）[8-10]应用LES方法对有拱度薄板机翼低速情况下的脉动压力进行计算，并结合FW-H方程对辐射噪声进行了计算。计算得到机翼表面导边区域压力场的频谱和展向相关性均与试验吻合较好，但低频域附近较差。远场声压谱与试验结果很吻合，其引入的有限弦长修正虽然比较小，但能进一步提高准确度。

Jean-François和Klaus（2009）[11]用DES对后台阶流动的脉动压力进行了计算，计算得到的脉动压力主频率与试验吻合很好，功率谱与经验模型一致。

张楠等人（2008-2011）[12-16]通过LES结合FW-H声学类比方法，计算了两类孔穴的流激噪声问题以及五种不同尺寸的方形孔腔在水中的流动特征及流激噪声。还基于LES和Kirchhoff积分，对孔腔流动的发声机理进行了分析。另外，利用大涡模拟计算了SUBOFF主、附体的表面压力分布，并对平板及水下航行体几个离散点的脉动压力进行了计算，计算结果与试验结果十分吻合，具有较高精度；平板脉动压力与试验值差异小于5 dB，比较可靠。近年来，张楠等人[23-25]又建立了大涡模拟结合渗流FW-H方程、Powell涡声方程的流激噪声计算方法，详细比较了原初FW-H方程、渗流FW-H方程、Powell涡声方程与Kirchhoff方程的数学内涵与计算精度和计算效率，为流声耦合研究提供了坚实的技术支撑。

张晓龙等人（2014）[17]采用大涡模拟方法（LES）结合四种亚格子涡模型与四套网格，对平壁面湍流脉动压力进行了数值计算，分析了涡旋结构与近壁面流速分布，研究了亚格子涡模型与网格数量对计算结果的影响，并与试验结果进行了定量与定性的比较分析，详细讨论了平壁面湍流脉动压力频谱计算值与试验值之间的差异。同时，验证了数值计算方法的可靠性。

其后，张晓龙等人（2014）[18]在已有工作[17]的基础上，采用大涡模拟方法（LES）结合动态亚格子涡模型（DSL）及千万量级的精细网格，对平板壁面湍流脉动压力及其波数—频率谱进行了数值计算，并与Abraham试验结果进行了定量与定性的对比验证分析。探讨了湍流脉动压力变化规律及其相似律，基于Fourier变换计算得到了湍流脉动压力波数—频率谱，并详细讨论了当传感器阵列沿流向布置时，壁面湍流脉动压力及其波数—频率谱计算值与试验值之间的差异。结果表明，计算结果与试验结果吻合良好，计算方法合理。这从湍流脉动压力尤其是湍流脉动压力波数—频率谱的角度进一步验证了数值计算方法的可靠性，为今后复杂几何模型壁面湍流脉动压力及其波数—频率谱的计算研究工作奠定了基础。同时需要指出，上述工作主要还是局限于对传感器阵列沿流向布置时的平板湍流脉动压力波数—频率谱进行计算分析研究。对于更复杂流动条件影响下（如：自由来流方向与传感器阵列呈一定角度时或传感器阵列处于逆压梯度区时）湍流脉动压力及其波数—频率谱特性，有待于开展进一步的研究分析。

总的来看，一方面，湍流脉动压力及其波数—频率谱的研究主要还是以试验测试为主，并且相关试验研究局限于采用沿流向布置的传感器线阵对湍流脉动压力及其波数—频率谱进行测量，自由来流方向与传感器阵列存在夹角情况下湍流脉动压力及其波数—频率谱的测量以及基于传感器面阵对湍流脉动压力及其波数—频率谱进行测量的试验研究均属罕见；另一方面，随数值计算方法的日趋成熟和计算能力的提高，有学者开展单点湍流脉动压力的数值计算研究。尤其是近来，也有学者开始开展基于监测点阵列的，多点湍流脉动压力及其波数—频率谱的计算与验证分析研究。但是，如前所述，多点湍流脉动压力及其波数—频率谱的计算研究主要还是局限于传感器阵列沿流向布置等简单流动条件。

本文在已有工作的基础上[17-18]，将基于大涡模拟方法，对自由来流角度影响下的壁面湍流脉动压力及其波数—频率谱展开数值计算分析研究。

1 计算方法

1.1 大涡模拟方法

大涡模拟（LES）的主要思想是：将湍流分解为可解尺度湍流运动（包含大尺度脉动）和不可解尺度湍流运动（包含所有小尺度脉动），并且认为，大尺度运动几乎包含所有的能量，而小尺度运动主要起能量耗散作用，几乎不受流场边界形状或平均运动的影响，近似认为是各向同性的。然后，小尺度运动对大尺度运动的作用通过建立模型（即亚格子涡模型）来实现，从而使运动方程封闭。对可解尺度运动则直接进行数值求解。

物理空间的滤波过程可表示如下：

滤波后的控制方程（连续性方程和N-S方程）为：

其中：σij为分子粘性引起的应力张量，τij为亚格子应力张量需要用亚格子涡模型进行模拟。 本文采用 DSL 亚格子涡模型进行计算，该模型由 Germano（1991）[19]提出，后来，Lilly（1992）[20]应用最小二乘法又对其作了改进。它通过局部计算涡粘性系数来尽可能地反映实际流动情况，通过对最小可解尺度的信息进行采样，然后利用这些信息来模拟亚格子尺度应力。此模型在接近壁面边界时给出了正确的渐近特性，因此也就不需要阻尼函数或者间歇函数，而且此模型还能够考虑逆散射的影响。其涡粘性系数由下式给出：

其中：Lij为可解的湍流应力，它表征介于网格滤波宽度与测试滤波宽度之间的雷诺应力的贡献。Mij是一个与滤波宽度和应变率张量有关的中间量。

1.2 湍流脉动压力波数—频率谱及其计算分析方法

目前湍流脉动压力的分析主要还是采用傅里叶分析来实现时间—空间和波数—频率域之间的转换，进而能够在波数—频率域内研究湍流脉动信号的统计特性。湍流脉动压力波数—频率谱定义为湍流脉动压力时—空信号的相关函数在时间和空间内的傅里叶变换，数学表达式为：

在实际中，通常通过对湍流脉动压力离散时空信号进行快速傅里叶变换（FFT），然后对其幅值的平方进行系综平均得到湍流脉动压力的波数—频率谱[3]。此时，湍流脉动压力波数—频率谱表达式如下：

其中：符号〈〉代表期望值，pm表示第m个传感器测得的脉动压力，N为时间结点数，M为传感器个数，Δx为传感器间距，Δt为时间步长：

Wt（tn）和Wx（xm）均为窗函数，本文采用汉宁窗（Hanning window）：

则为窗常数。

1.3 计算模型、网格及数值方法

计算模型如图1所示，计算采用平板模型，导边为圆弧形，平板尺度与Abraham湍流脉动压力测量试验中的试验段尺度相当，板长为L=2.10 m，展向长度a=0.304 8 m，监测点阵列由48个与自由来流方向呈一定角度（45°和90°）且等间距布置的监测点组成，监测点阵列起始点距导边距离x0=1.63 m。三个计算工况与Abraham脉动压力测量试验一致，三个工况下自由来流速度分别为U0=3.1 m/s，4.6 m/s和 6.1 m/s，起始监测点处对应的局部雷诺数分别为 Re=4.47×106，6.70×106和 1.02×107。

本节采用三维模型计算，计算区域为平板导边向前三倍板长3L，随边向后五倍板长5L，外边界距平板表面约三倍板长3L；计算域采用结构化网格，网格剖分形式采用C-H型，网格数量1 000万，计算区域网格如图2所示。

边界条件设为速度入口、压力出口以及无滑移壁面边界条件；时间项采用二阶隐式格式离散，动量方程采用限界中心差分格式离散，压力速度耦合采用SIMPLE算法。计算时间步长Δt=10-4s，壁面y+≈1。

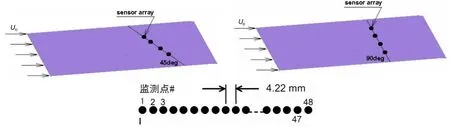
图1 平板模型及监测点阵列布置示意图Fig.1 The configuration of the sensor array on the plate

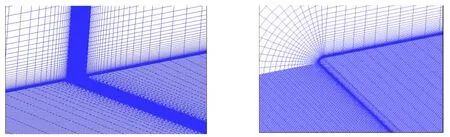
图2 平板计算区域网格划分图Fig.2 The computational domain and grid

2 计算结果与分析

图3-11给出了监测点阵列与自由来流呈不同夹角布置时，湍流脉动压力波数—频率谱的三维视图；图12-14给出了计算得到的平板湍流脉动压力波数—频率谱。为便于进一步的比较分析，表1-3给出了不同来流速度和自由来流夹角下湍流脉动压力波数—频率谱各主要参数的详细对比数据。

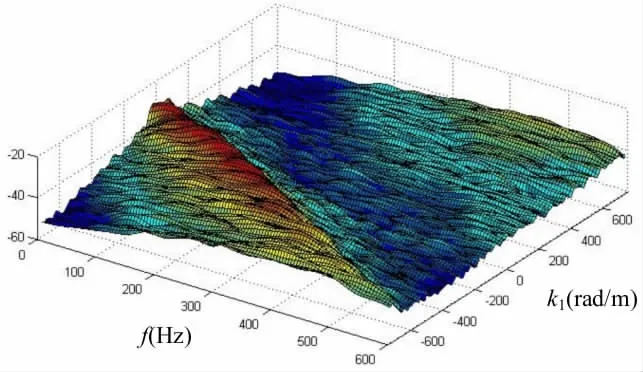
图3 湍流脉动压力波数—频率谱三维视图 （U0=6.1 m/s，0°） Fig.3 Three dimensional plot of the computed wavenumber-frequency spectra (U0=6.1 m/s，0°)

图5 湍流脉动压力波数—频率谱三维视图（U0=6.1 m/s，90°）Fig.5 Three dimensional plot of the computed wavenumber-frequency spectra(U0=6.1 m/s，90°)

图6 湍流脉动压力波数—频率谱三维视图（U0=4.6 m/s，0°）Fig.6 Three dimensional plot of the computed wavenumber-frequency spectra(U0=4.6 m/s，0°)

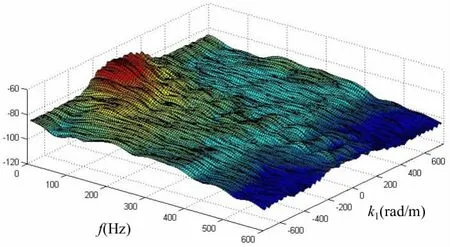
图7 湍流脉动压力波数—频率谱三维视图（U0=4.6 m/s，45°）Fig.7 Three dimensional plot of the computed wavenumber-frequency spectra(U0=4.6 m/s，45°)

图8 湍流脉动压力波数—频率谱三维视图 （U0=4.6 m/s，90°）Fig.8 Three dimensional plot of the computed wavenumber-frequency spectra(U0=4.6 m/s，90°)

图9 湍流脉动压力波数—频率谱三维视图 （U0=3.1 m/s，0°） Fig.9 Three dimensional plot of the computed wavenumber-frequency spectra (U0=3.1 m/s，0°)

图10 湍流脉动压力波数—频率谱三维视图 （U0=3.1 m/s，45°）Fig.10 Three dimensional plot of the computed wavenumber-frequency spectra(U0=3.1 m/s，45°)

图11 湍流脉动压力波数—频率谱三维视图（U0=3.1 m/s，90°）Fig.11 Three dimensional plot of the computed wavenumber-frequency spectra(U0=3.1 m/s，90°)

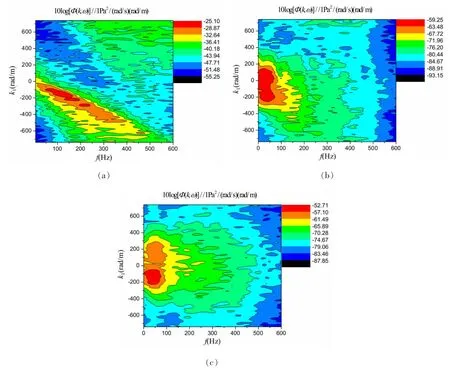
图12 不同来流角度下湍流脉动压力波数—频率谱（U0=6.1 m/s）：（a） 0°；（b） 45°；（c） 90°Fig.12 Computed wavenumber-frequency spectra under various free-stream velocity angles(U0=6.1 m/s):(a)0°;(b)45°;(c)90°

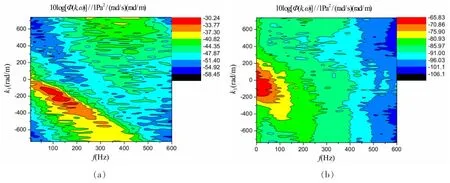
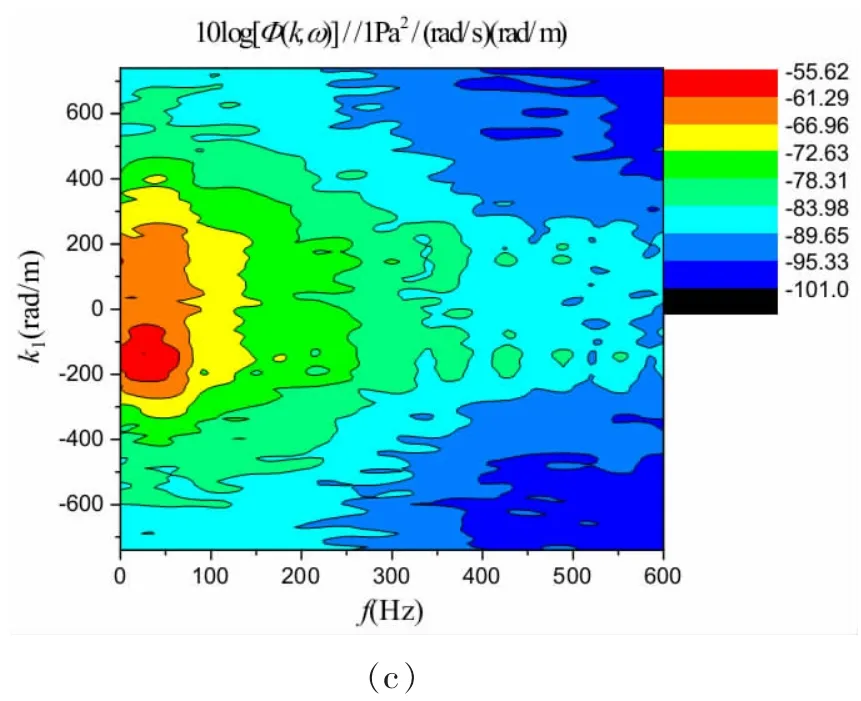
图13 不同来流角度下湍流脉动压力波数—频率谱（U0=4.6 m/s）：（a） 0°；（b） 45°；（c） 90°Fig.13 Computed wavenumber-frequency spectra under various free-stream velocity angles(U0=4.6 m/s):(a)0°;(b)45°;(c)90°

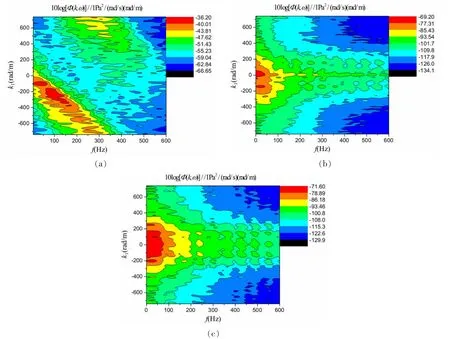
图14 不同来流角度下湍流脉动压力波数—频率谱（U0=3.1 m/s）：（a） 0°；（b） 45°；（c） 90°Fig.14 Computed wavenumber-frequency spectra under various free-stream velocity angles(U0=3.1 m/s):(a)0°;(b)45°;(c)90°

表1 湍流脉动压力波数—频率谱各主要参数（U0=6.1 m/s）Tab.1 Parameters of the computed wavenumber-frequency spectra(U0=6.1 m/s)

续表1

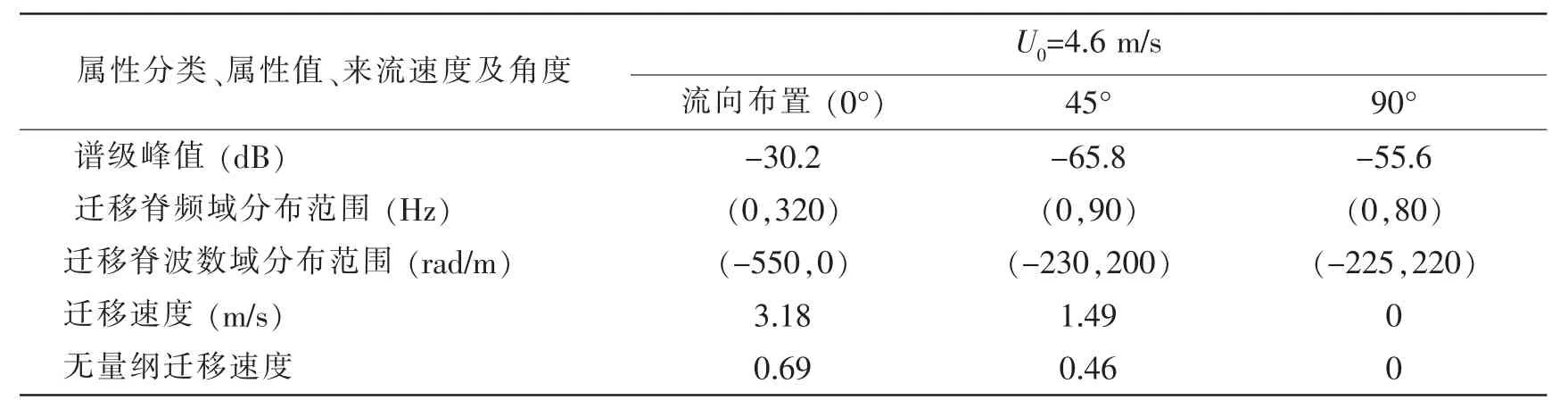
表2 湍流脉动压力波数—频率谱各主要参数（U0=4.6 m/s）Tab.2 Parameters of the computed wavenumber-frequency spectra(U0=4.6 m/s)

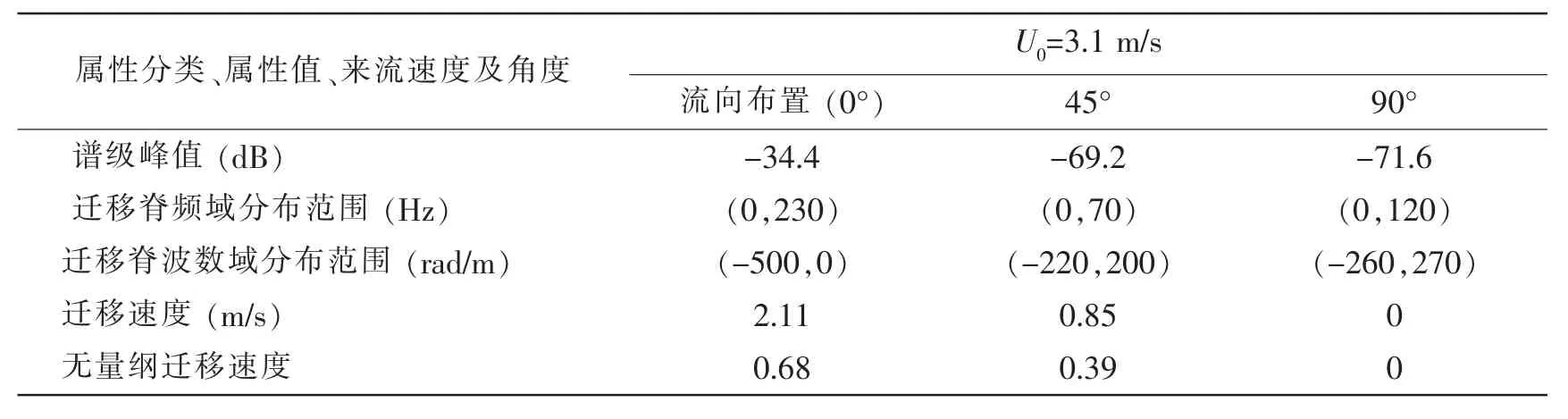
表3 湍流脉动压力波数—频率谱各主要参数（U0=3.1 m/s）Tab.3 Parameters of the computed wavenumber-frequency spectra(U0=3.1 m/s)

以下基于计算得到的图表数据，对自由来流角度下湍流脉动压力的波数—频率谱展开详细分析。

先讨论自由来流速度U0=6.1 m/s情况，从图3-5、图12及表1中数据可以看出，与流向布置（0°夹角）情况相比，当监测点阵列与流向存在夹角时，相应的波数-频率谱各项主要参数均发生明显变化。

首先，波数—频率谱的谱级峰值明显减小，监测点阵列与流向夹角45°和90°时，谱级峰值分别为-59.3 dB和-52.7 dB，相比于0°夹角情况分别减小34.2 dB和27.6 dB。这说明当监测点阵列与流向存在夹角时，监测点阵列所在纵剖面内的湍流能量明显减小，湍流能量主要沿流向分布。

其次，迁移脊在波数—频率域内的分布范围也明显减小，监测点阵列与流向夹角45°和90°时，波数—频率谱分布于频率的低频低波数范围，说明湍流能量主要集中在低频低波数范围。根据已有研究可知，此波数—频率范围对应湍流边界层中的大尺度涡[21-22]，同时这也说明与来流方向呈夹角的纵剖面内，湍流能量主要来自于较大尺度涡的贡献。

另外，从表1中的数据也可以看出，随监测点阵列与流向夹角的增加，迁移速度和无量纲迁移速度均明显减小。当监测点阵列与流向夹角90°时，迁移速度减小为0。迁移速度和无量纲迁移速度的变化原因在于：一方面，随夹角增大，是监测点阵列方向上的速度分量减小，从而直接导致迁移速度减小，当监测点阵列与流向夹角90°时，监测点阵列方向上来流速度分量为0，从而迁移速度减小为0；另一方面，自由来流在垂直于监测点阵列方向上存在横向速度分量，此横向速度分量对监测点阵列所在纵剖面内的波数—频率谱也产生影响。此两方面因素的综合作用最终导致湍流脉动压力迁移速度及无量纲迁移速度的显著变化。

图6-11、图13-14及表2-3给出了自由来流速度U0=4.6 m/s和U0=3.1 m/s、监测点阵列与自由来流呈不同夹角时的波数—频率谱计算结果。从表2-3中的对比数据可以看出，波数—频率谱变化规律与U0=6.1 m/s保持一致。当U0=4.6 m/s、监测点阵列与流向夹角45°和90°时，谱级峰值分别为-65.8 dB和-55.6 dB，比0°夹角情况分别减小35.6 dB和25.4 dB。波数—频率谱则分布于频率230的低频低波数范围。迁移速度和无量纲迁移速度明显减小，迁移速度分别为1.49、0，无量纲迁移速度分别为0.46、0。当U0=3.1 m/s、监测点阵列与流向夹角45°和90°时，谱级峰值分别为-69.2 dB和-71.6 dB，比0°夹角情况分别减小34.8 dB和37.2 dB。波数—频率谱均分布于频率的低频低波数范围。迁移速度和无量纲迁移速度亦明显减小，迁移速度分别为0.85、0，无量纲迁移速度分别为 0.39、0。

综合以上分析可以看出，在监测点阵列与自由来流方向存在夹角情况下，湍流脉动压力波数—频率谱的各项主要参数（包括：波数—频率谱的谱级峰值、迁移脊形态、迁移脊波数—频率域分布范围和迁移速度等）均发生了明显变化，说明监测点阵列布置方向对湍流脉动压力的波数—频率谱有显著影响。另外，由以上分析可知，边界层内湍流脉动压力的能量主要沿流向分布。因此，为了更加准确可靠地研究边界层内湍流脉动压力的主要统计特性及其波数—频率谱，传感器阵列或监测点阵列布置方向应与当地流向（局部剪应力线或摩擦力线）一致。

3 结论与展望

本文在已有工作的基础上，用大涡模拟方法，结合动态DSL亚格子涡模型及千万量级精细网格对不同来流速度下、监测点阵列与自由来流呈不同夹角布置时的湍流脉动压力及其波数—频率谱进行了计算，深入探讨了自由来流角度对湍流脉动压力及其波数—频率谱的影响，得到的主要结论如下：

（1）当监测点阵列与流向存在夹角时，波数—频率谱的谱级峰值明显减小，即监测点阵列所在纵剖面内的湍流能量明显减小，湍流能量主要沿流向分布。

（2）迁移脊在波数—频率域内的分布范围也明显减小，湍流能量主要集中在低频低波数范围。同时这也说明与来流方向呈夹角的纵剖面内，湍流能量主要来自于较大尺度涡的贡献。

（3）随监测点阵列与流向夹角的增加，迁移速度和无量纲迁移速度均明显减小。原因在于：一方面，随夹角增大，是监测点阵列方向上的速度分量减小，从而直接导致迁移速度减小；另一方面，横向速度分量对监测点阵列所在纵剖面内的波数—频率谱也产生影响。两方面因素的综合作用最终导致湍流脉动压力迁移速度及无量纲迁移速度的显著变化。

（4）由于自由来流角度对湍流脉动压力及其波数—频率谱影响显著，且边界层内湍流脉动压力的能量主要沿流向分布，因此，为了更加准确可靠地研究边界层内湍流脉动压力的主要统计特性及其波数—频率谱，传感器阵列或监测点阵列布置方向应与当地流向（局部剪应力线或摩擦力线）一致。

[1]Corcos G M.The structure of the turbulent pressure field in boundary layer flows[J].Journal of Fluid Mechanics,1964,18(3):353-378.

[2]Corcos G M.The resolution of turbulent pressure at the wall of a boundary layer[J].Journal of Sound and Vibration,1967,6(1):59-70.

[3]Abraham B M,Keith W L.Direct measurements of turbulent boundary layer wall pressure wavenumber-frequency spectra[J].Journal of Fluids Engineering,1998,120(3):29-39.

[4]Cipolla K M,Keith W L.Effects of pressure gradients on turbulent boundary layer wavenumber frequency spectra[J].AIAA Journal,2000,38(10):1832-1836.

[5]Cipolla K M,Keith W L.Measurements of the wall pressure spectra on a full-scale experimental towed array[J].Ocean Engineering,2008,35(3):1052-1059.

[6]Bonness W K,Capone D E,Hambric S A.Low wavenumber turbulent boundary layer wall pressure measurments from vibration data on a cylinder in pipe flow[J].Journal of Sound and Vibration,2010,329:4166-4180.

[7]Manoha E,Troff B,Sagaut P.Trailing-edge noise prediction using large-eddy simulation and acoustic analogy[J].AIAA Journal,2000,38(4):575-583.

[8]Wang Meng.Computation of trailing-edge flow and noise at low Mach number using LES and acoustic analogy[R].Annual Research Briefs,Center for Turbulence Research,Stanford University,1998.

[9]Wang Meng,Parviz Moin.Computation of trailing-edge flow and noise using large-eddy simulation[J].AIAA Journal,2000,38(12):2201-2209.

[10]Wang Meng,Moreau S,Iaccarinoand G,Roger M.LES prediction of wall-pressure fluctuations and noise of a low-speed airfoil[J].International Journal of Aeroacoustics,2009,8(3):177-198.

[11]Dietiker J F,Hoffmann K A.Predicting wall pressure fluctuation over a backward-facing step using detached eddy simulation[J].Journal of Aircraft,2009,46(6):2115-2020.

[12]张 楠,沈泓萃,姚惠之,朱锡清,俞孟萨.孔穴流激噪声的计算与验证研究[J].船舶力学,2008,12(5):799-805.Zhang Nan,Shen Hongcui,et al.Validation and calculation of flow induced noise of cavity[J].Journal of Ship Mechanics,2008,12(5):799-805.

[13]张 楠,沈泓萃,姚惠之,田于逵,谢 华.水下航行体壁面脉动压力的大涡模拟研究[J].水动力学研究与进展,2010,25(1):106-112.Zhang Nan,Shen Hongcui,et al.Large eddy simulation of wall pressure fluctuations of underwater vehicle[J].Chinese Journal of Hydrodynamics,2010,25(1):106-112.

[14]张 楠,沈泓萃,朱锡清,姚惠之,谢 华.三维孔腔流激噪声的大涡模拟与声学类比预报与验证研究[J].船舶力学,2010,14(1-2):181-190.Zhang Nan,Shen Hongcui,et al.Validation and prediction of flow induced noise of 3-dimensional cavity with large eddy simulation and acoustic analogy[J].Journal of Ship Mechanics,2010,14(1-2):181-190.

[15]张 楠,沈泓萃,朱锡清,姚惠之.基于大涡模拟和Kirchhoff积分方法的孔腔流动发声机理分析[J].船舶力学,2011,15(4):427-434.Zhang Nan,Shen Hongcui,et al.Analysis of the mechanism of cavity flow induced noise with large eddy simulation and acoustic analogy[J].Journal of Ship Mechanics,2010,15(4):427-434.

[16]张 楠.孔腔流动和流激噪声机理及耦合计算方法研究[D].无锡:中国船舶科学研究中心,2010.

[17]张晓龙,张 楠,吴宝山.壁面涡旋结构与湍流脉动压力的大涡模拟研究[J].船舶力学,2014,18(8):871-881.Zhang Xiaolong,Zhang Nan,Wu Baoshan.Computation of wall pressure fluctuations and vortical structures using large eddy simulation[J].Journal of Ship Mechanics,2014,18(8):871-881.

[18]张晓龙,张 楠,吴宝山.平壁面湍流脉动压力及其波数-频率谱的大涡模拟计算分析研究[J].船舶力学,2014,18(10):1151-1164.Zhang Xiaolong,Zhang Nan,Wu Baoshan.Computation of turbulent wall pressure fluctuation and its wavenumber-frequency spectrum using large eddy simulation[J].Journal of Ship Mechanics,2014,18(8):1151-1164.

[19]Germano M,Piomelli U,Cabot W H.A dynamic subgrid-scale eddy viscosity model[J].Phys.Fluids,1991,A3(7):1760-1765.

[20]Lilly D K.A proposed modification of the germano subgrid scale closure method[J].Phys.Fluids,1992,A4(3):633-635.

[21]Haecheon Choi,Parviz Moin.On the space-time charateristics of wall pressure fluctuations[J].Phys.Fluids,1990,A2(8):1450-1460.

[22]Farabee T M,Casarella M J.Spectral features of wall pressure fluctuations beneath turbulent boundary layers[J].Phys.Fluids,1991,A3(10):2410-2420.

[23]张 楠,王 星,谢 华,李 亚.流激噪声数值计算方法及声学积分面影响性研究[J].船舶力学,2016,20(7):892-908.Zhang Nan,Wang Xing,Xie Hua,Li Ya.Research on numerical simulation approach for flow induced noise and the influence of the acoustic integral furface[J].Journal of Ship Mechanics,2016,20(7):892-908.

[24]Zhang Nan,Xie Hua,Wang Xing,Wu Baoshan.Computation of vortical flow and flow induced noise by large eddy simulation with FW-H acoustic analogy and Powell vortex sound theory[J].Journal of Hydrodynamics,2016,28(2):255-266.

[25]张 楠,李 亚,王志鹏,王 星,张晓龙.基于LES与Powell涡声理论的孔腔流激噪声数值模拟研究[J].船舶力学,2015,19(11):1393-1408.Zhang Nan,Li Ya,Wang Zhipeng,et al.Numerical simulation on the flows induces noise of cavity by LES and powell vortex sound theory[J].Journal of Ship Mechanics,2015,19(11):1393-1408.

Investigating the effects of free-stream velocities on turbulent wall pressure fluctuations and their wavenumber-frequency spectra at high Reynolds numbers using Large Eddy Simulation

ZHANG Xiao-long,ZHANG Nan,WU Bao-shan
(National Key Laboratory of Hydrodynamics,China Ship Scientific Research Center,Wuxi 214082,China)

Turbulent wall pressure fluctuations beneath turbulent boundary layers are important sources of flow noise.The computation and discussion of wall pressure fluctuations and their wavenumber-frequency spectra are hot topics in the field of flow-acoustic coupling.In this paper,wall pressure fluctuations of different geometries at high Reynolds numbers and their wavenumber-frequency spectra are computed using large eddy simulation(LES)with appropriate sub-grid scale model,grid number and discretization methods,in order to investigate the effects freestream velocities.The Reynolds number is up to Re=1.02×107and the computed results are discussed in detail based on previous research by the author.And,some fundamentals of the numerical simulation are presented,including the philosophy of LES,formulations of sub-grid scale models,discretization methods and boundary conditions.Secondly,the definition of wavenumber-frequency spectra and the approaches of their analysis and computation are demonstrated.Finally,turbulent wall pressure fluctuations as well as their wavenumber-frequency spectra under different freestream velocities are computed and analyzed in detail.The results show a remarkable change of the wavenumberfrequency spectra as affected by various freestream velocity angles and the kinetic energy of turbulent wall pressure fluctuations is mainly distributed along the flow direction.Based on detailed analysis of the computed results,it is recommended that the sensor array should be allocated along the local flow direction(or the local wall shear stress),in order to study the statistical characters or the wavenumber-frequency spectra more accurately.

turbulent wall pressure fluctuations;wavenumber-frequency spectrum;effects of free-stream velocities;LES

O35

A

10.3969/j.issn.1007-7294.2017.11.002

1007-7294（2017）11-1323-13

2017-08-12

张晓龙（1988-），男，硕士，中国船舶科学研究中心工程师，E-mail：xlz_zhang@hotmail.com；

张 楠（1977-），男，博士，中国船舶科学研究中心研究员。