基于声场波数谱特征的深度估计方法

刘坤 刘福臣 田玲爱 林旺生

（声纳技术重点实验室，杭州，310023）

基于声场波数谱特征的深度估计方法

刘坤 刘福臣 田玲爱 林旺生

（声纳技术重点实验室，杭州，310023）

为了估计目标深度、区分水下水面目标，提出了水平接收基阵获取声场波数谱和基于声场垂直波数谱特征的深度估计方法。仿真结果表明，在高信噪比情况下，该方法估计目标深度是可行的。

简正波模态；声场波数谱；深度估计；目标分类

水中目标分类在军事防御及进攻上具有重要作用，深度估计是水面目标和水下目标分类[1-4]的一个直观的判据。总体来说，目标深度估计是一个水声领域的普遍难题，目前，目标深度估计大多采用匹配场方法进行，但该方法面临着声场环境适配问题。目标特征与海洋信道之间的关联十分紧密，水声探测系统接收到的目标信号都是目标源激发信号与信道多途响应耦合后的信号，根据声场简正波理论，接收信号的声场波数谱为目标深度包络与接收深度包络的调制谱，该谱同时反映了目标深度信息和接收深度信息，因此波数谱上的包络特征结合基阵本身的深度信息可以估计出目标深度。

1 声场垂直波数谱特征的深度估计

等声速波导中，令海深为D，海水声速为c0，密度为ρ0，则第l阶简正波模态的垂直波数理论值γl及水平波数理论值kl，如下式[5]所示：

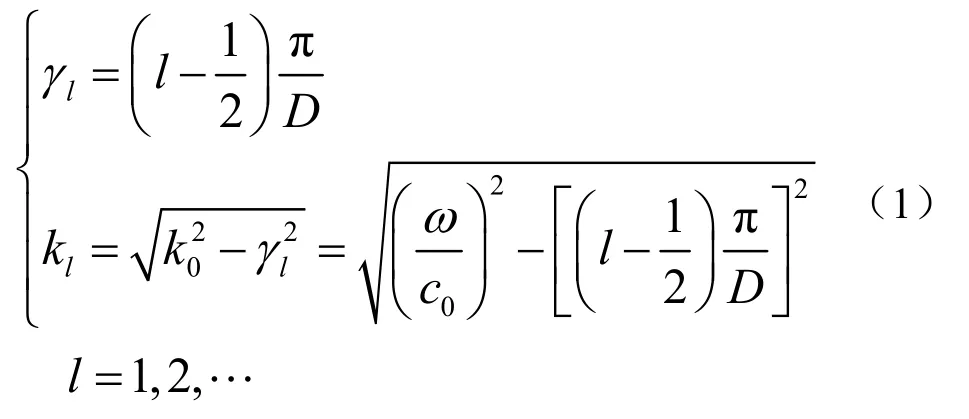
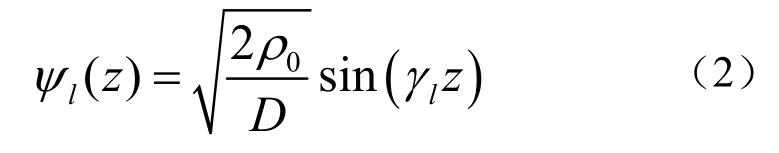
声压场的简正波表达式为：

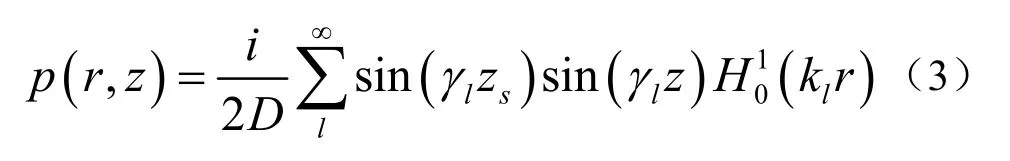
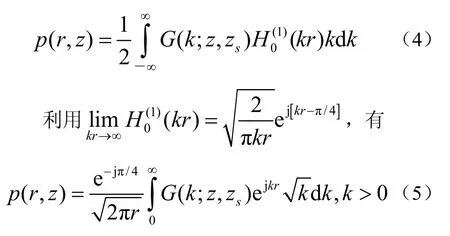
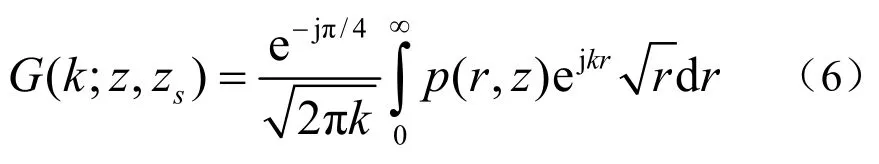
在等声速波导中，声压表达式为式（3），将式（3）代入式（6），并利用模深度函数的正交性，可以得到波数谱G(kl;z,zs)的模为：

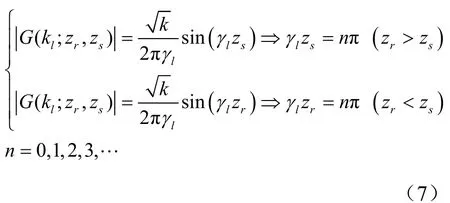
从式（7）可以看到，声场垂直波数谱的模是sin(γlzs)或sin(γlzr)调制的，而从式（1）容易知道，垂直波数γl是等间隔分布的，对垂直波数进行周期性分析，即由垂直波数谱相邻谱线对应的垂直波数间隔可对目标深度或接收深度进行估计，即

由此可以看出：当接收深度比声源深度浅时，波数谱反映了接收深度的信息；当接收深度比较深或置于海底时，波数谱反映了目标深度信息。

在理想条件下，各阶模态垂直波数是等间隔均匀分布的，可以按照式（8）利用相邻垂直波数差进行深度估计。在实际情况下，由于目标深度位于某阶模态的模深度函数零点，或由于传播衰减导致某阶模态较弱，则无法利用式（8）进行深度估计，但是由于声场垂直波数谱的模是sin(γlzs)或sin(γlzr)调制的，则可以利用频谱分析的方法对zs和zr估计，得到目标深度估计曲线，其最大值对应着目标深度或接收深度。

2 水平接收基阵的声场波数谱获取

获取声场波数谱G(k;z,zs)（即公式（6）），对距离r和波数k等间隔进行离散，快速Fourier变换可有效用于逆Hankel变换和Hankel变换，采样间隔Δr和Δk满足以下关系

距离和波数的离散点分别为

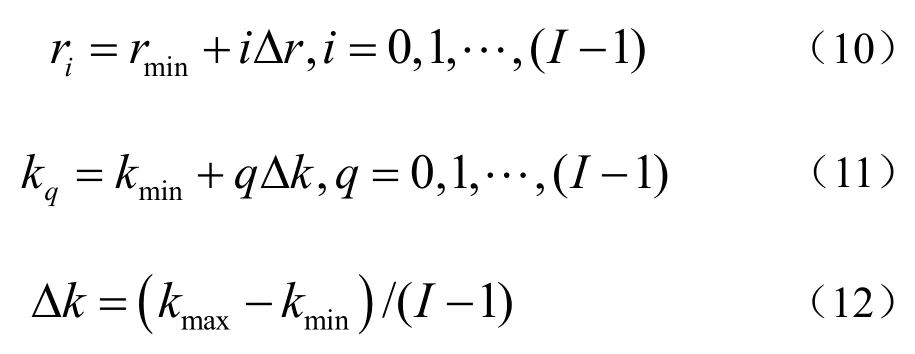
式中，I为离散Fourier变换的序列长度，取为2的整数次幂。q为波数取样点序号，因而有

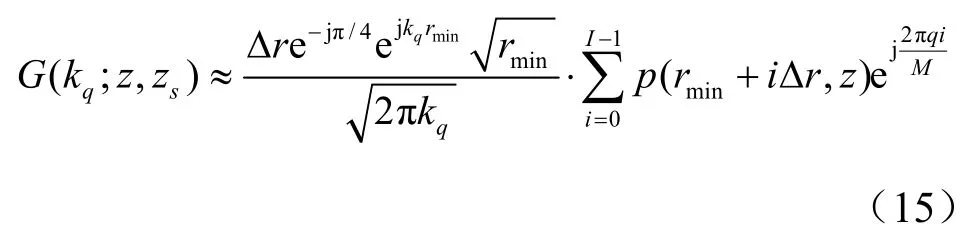
水平波数与垂直波数的关系为：

将式（16）代入式（15），得到声场垂直波数谱G(γl;z,zs)：

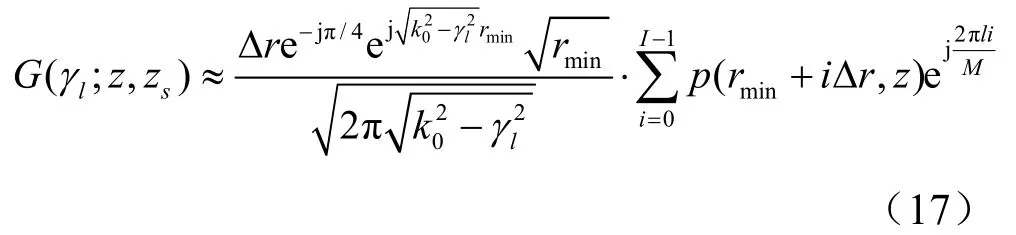
为保证式（17）的波数分辨率，在进行距离水平波数Hankel变换时，需要较大的距离采样。当目标越接近基阵端射时，不同阵元接收信号的声程差越大，越容易进行距离水平波数Hankel变换，越容易得到声场波数谱；对于不同方位到达的信号来说，为了获得较大的距离采样，需要对声压信号场进行距离插值；而当目标接近基阵正横时，由于声程差减小至0，则不能获得声场波数谱。

3 算法流程

根据上述方法，下面给出基于声场波数谱特征的深度估计算法流程，如图1所示。

图1 算法流程

首先，对基阵数据进行FFT得到声场转移函数；进行距离水平波数Hankel变换，得到声场水平波数谱；通过水平波数垂直波数变换，得到声场垂直波数谱；对垂直波数谱进行周期性分析，得到目标深度。

4 仿真分析

4.1 水面目标和水下目标深度估计

仿真条件：等声速波导，波导水文参数如图2所示。

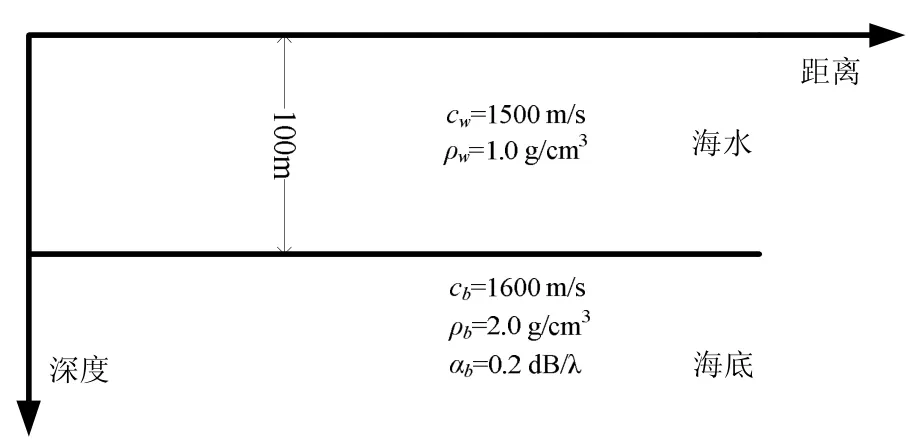
图2 等声速波导

4.1.1 水面目标

目标位于接收阵端射方位，目标与接收位置水平距离1 km，目标深度5 m，接收深度100 m，频率750 Hz，水平接收基阵阵元个数384，阵元间距1 m。不考虑噪声干扰的情况下，水面目标声场垂直波数谱包络如图3所示，相邻两个垂直波数估计值为0.2774和0.8028，垂直波数差为0.5754，按照深度估计公式（8），估计目标深度为5.5 m，估计值与真实值相吻合。

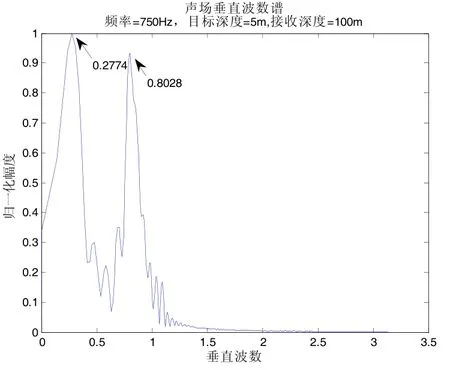
图3 水面目标声场垂直波数谱

利用频谱分析方法估计出目标深度曲线如图4所示。其中，虚线为目标真实深度，估计目标深度为5.4 m，可以看到估计值与真实值相吻合。

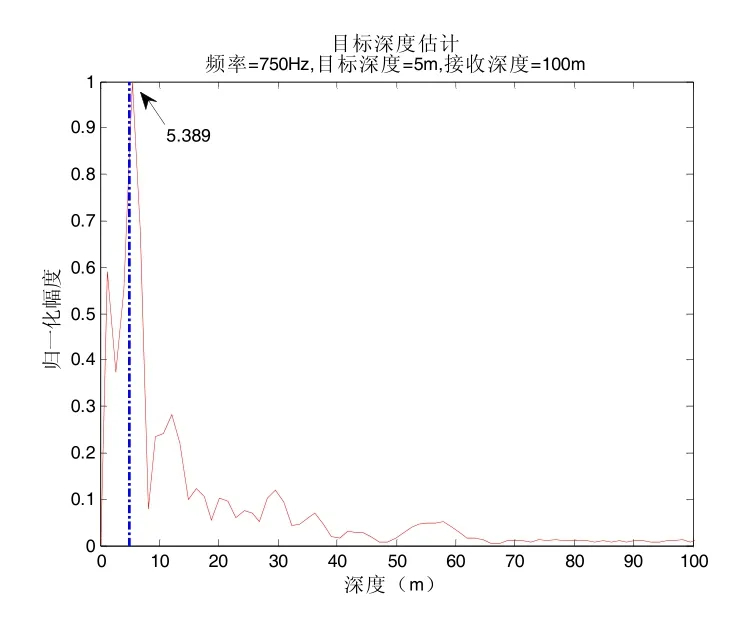
图4 目标深度估计曲线

4.1.2 水下目标

目标位于接收阵端射方位，目标与接收位置水平距离1 km，目标深度50 m，接收深度100 m，频率750 Hz，水平接收基阵阵元个数384，阵元间距1 m。不考虑噪声干扰的情况下，水下目标声场垂直波数谱包络如图5所示，相邻两个垂直波数估计值为0.9506、1.016和1.077，垂直波数差为0.0654和0.0610，按照深度估计公式（8），估计目标深度为48.0 m和51.5 m，估计值与真实值相吻合。对水下目标的声场垂直波数谱包络进行周期性估计，估计出目标深度如图6所示。其中，虚线为目标真实深度，排除深度为1.5 m的伪峰（由基阵本身深度引入），估计目标深度为50.7 m，估计值与真实值相吻合。

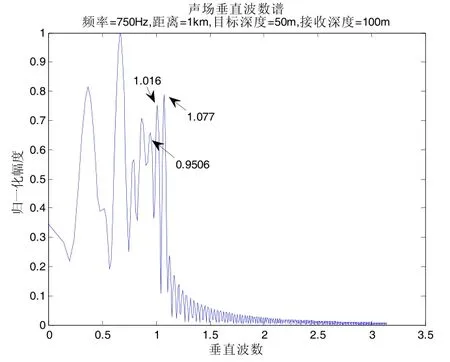
图5 水下目标声场垂直波数谱

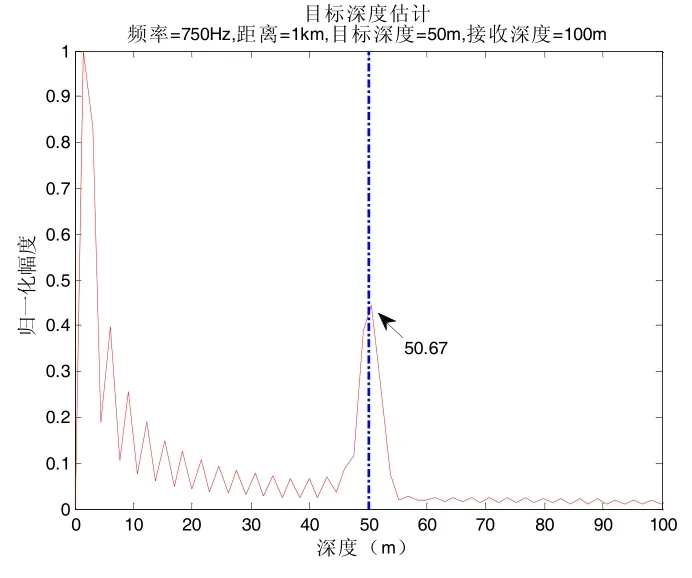
图6 目标深度估计值

4.2 不同海深、不同频率、不同接收距离、不同接收深度和不同目标深度情况

等声速波导，目标位于接收阵端射方位，水平接收基阵阵元个数384，阵元间距1 m，不考虑噪声干扰的情况下，不同海深、频率、接收距离、接收深度和目标深度条件下，利用目标声场波数谱包络特征估计的目标深度值如表1所示，同时给出其中几个仿真条件下，目标深度估计曲线，如图7所示。

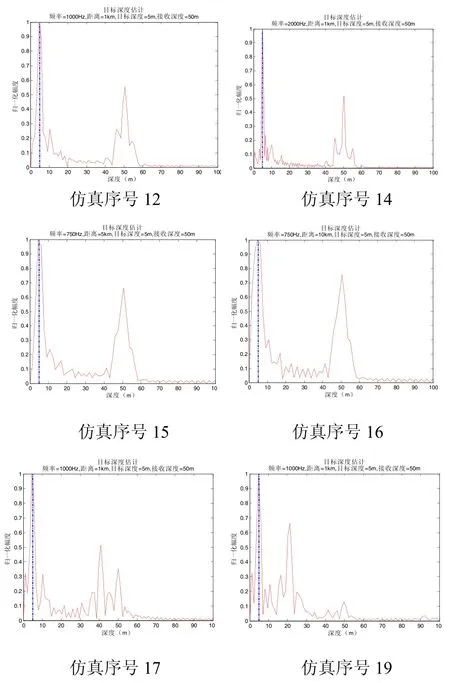
图7 不同条件下，目标深度估计值

从上面仿真可以看到：

①不考虑噪声干扰时，不同海深、频率、接收距离、接收深度和目标深度条件下，利用声场波数谱包络特征可以估计出目标深度值，估计误差在10%以内。

②当接收深度位于海底，目标深度小于接收深度时，利用声场波数谱包络特征只能估计出目标深度。

③当接收深度大于目标深度，但接收深度不是位于海底时，由于波数谱为目标深度包络与接收深度包络的调制谱，所以，利用声场波数谱包络特征可以估计出目标深度和接收深度。

④当目标为水面目标，接收深度较深时，随着目标频率越高，估计精度相对越高，主要原因是目标频率越高，声场模态数目越多，声场垂直波数谱包络周期性越明显，对包络进行周期性估计越容易。

⑤当接收深度大于目标深度，利用声场波数谱包络特征估计出的目标深度精度与目标距离无关。

⑥当海深逐渐减小时，声场模态数目逐渐减小，模态多途影响逐渐加重，对目标的声场垂直波数谱包络进行周期估计，估计声源深度时，会出现一定的伪峰。

4.3 水面目标不同波导水文情况

不考虑噪声干扰的情况下，分别考察正梯度波导、负梯度波导和负跃层波导情况下，利用目标声场波数谱包络特征进行目标深度估计，三种波导水文参数如图8所示。

目标位于接收阵端射方位，目标深度5 m，接收深度100 m，目标与接收位置水平距离5 km，频率750 Hz，水平接收基阵阵元个数384，阵元间距1 m。

图8 不同波导情况

表2 不同波导情况下，目标深度估计值

从表2的仿真结果可以看到：不考虑噪声干扰的情况下，在正梯度、负梯度和负跃层波导中，通过目标声场垂直波数谱包络周期性特征，可以大致估计出目标深度。这对于目标分类来说，具有一定的指导作用。

4.4 水面目标不同信噪比情况

下面考虑白噪声干扰的情况，分别考察不同信噪比情况下，利用目标声场波数谱包络特征进行目标深度估计的情况。

仿真条件：等声速波导，波导水文参数如图2所示，目标位于接收阵端射方位，目标与接收位置水平距离5 km，目标深度5 m，接收深度100 m，频率750 Hz，水平接收基阵阵元个数384，阵元间距1 m。

从表3的仿真结果可以看到：随着信噪比的升高，通过声场垂直波数谱特征估计出目标深度误差逐渐减小；利用目标声场垂直波数谱特征估计目标深度，需要较高的信噪比，在信噪比大于9 dB时，才能保证估计精度。

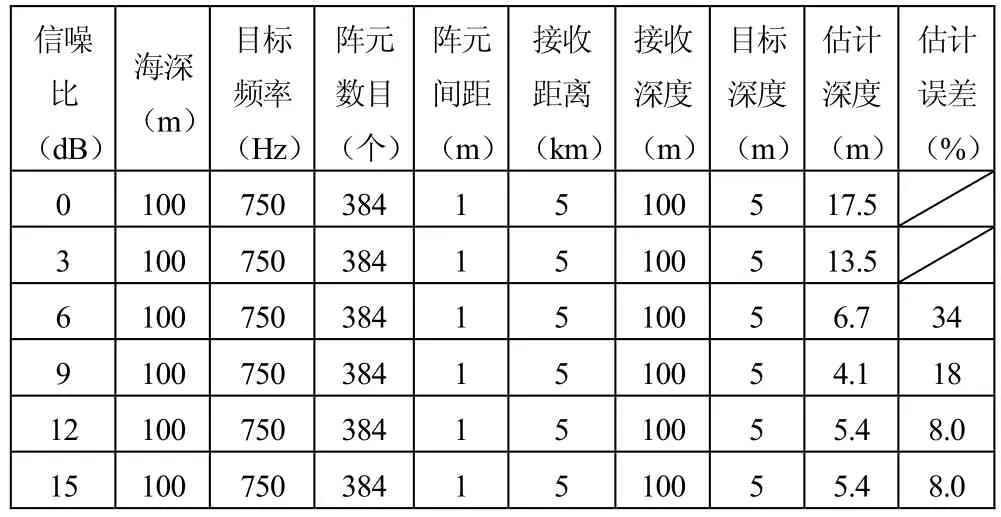
表3 不同信噪比下，目标深度估计值

5 结论

本文结合声场简正波和波数积分理论，介绍了基于声场垂直波数谱特征的深度估计方法；给出了水平接收基阵获取声场波数谱的方法；仿真了不同海深、频率、接收距离、接收深度、目标深度，波导水文和信噪比条件下目标深度估计情况，仿真结果表明：在高信噪比情况下，利用声场波数谱特征估计目标深度是可行的；在负梯度和负跃层恶劣波导水文条件下，利用该方法可以大致估计出目标深度，对于目标分类来说，具有一定的指导意义。

[1] CREAMER D B. Scintillating shallow-water waveguides[J]. Journal of Acoustical Society of American, 1996, 99 (6): 2825-2838.

[2] PREMUS V. Modal scintillation index: a physicsbased statistic for acoustic source depth discrimination[J]. Journal of Acoustical Society of American, 1999, 105 (4): 2170-2180.

[3] NICOLAS B, MARS J, LACOUME J-L. Source depth estimation using matched field processing and frequencywavenumber transform[C]. In 12th European Signal Processing conference, Vienna, 2004.

[4] BONNEL J, GERVAISE C, ROUX P, et al. Modal depth function estimation using time-frequency analysis[J]. Journal of Acoustical Society of American, 2011, 130 (1): 61-71.

[5] JENSEN F B, KUPERMAN W A, PORTER M B, et al . Computational ocean acoustics[M]. New York: American Institute of Physics, 1994.

[6] BREKHOVSKIKH L M, LYSANOV YU. Fundamentals of ocean acoustics springer-verlag[M]. New York, 1991.