翻边开孔对矩形板振动频率的影响

王文胜，魏豪杰，侯中华，王占磊，梅 群

（河南科技大学 工程力学系，河南 洛阳 471023）

翻边开孔对矩形板振动频率的影响

王文胜，魏豪杰，侯中华，王占磊，梅 群

（河南科技大学 工程力学系，河南 洛阳 471023）

研究了带有翻边长圆开孔矩形板的振动特性。利用ANSYS软件建立翻边开孔矩形板的参数化有限元模型，获得不同开孔参数（开孔率、翻边高度、开孔位置及转动）情况下结构的前两阶固有频率。在此基础上数值分析翻边开孔参数对矩形板前两阶固有频率的影响，发现翻边开孔能显著改变矩形板的固有频率，且与板的边界约束条件有很大关系。研究结果为实际结构的翻边开孔设计提供了参考。

翻边；长圆孔；矩形板；固有频率

0 引 言

在实际工程结构中，为了实现结构的方便观测、维修以及减重或者性能优化等方面的需求，在船舶、航空、建筑工程等领域，经常需要在板上开通风孔、管线过孔或减重孔等。结构开孔后会在孔周边出现应力集中现象，降低了构件的静强度。而且开孔后结构的质量和刚度分布特性会发生改变，对结构的固有频率或振型等力学性能有较大影响。因此开孔后结构的力学性能分析一直是研究热点问题[1-6]，在工程结构设计中具有重要意义。

开孔矩形板的振动问题受到国内外学者的广泛关注，主要考虑了带有圆形、椭圆或矩形等开孔形状矩形板的动力性能分析[7-9]。而实际工程中如果采用冲压开孔的方法在结构上开孔，产生开孔的同时可以在孔边形成一定高度的翻边，对于带有翻边开孔的矩形板动力性能分析的研究工作似未见报道。本文以带有翻边长圆形开孔的矩形板为研究对象，采用ANSYS软件建立翻边开孔矩形板的参数化模型，分析不同开孔参数（开孔率、翻边高度、开孔位置及开孔转动）对矩形板第一、第二阶固有频率的影响及变化规律，为实际结构的翻边开孔设计提供参考。

1 薄板振动理论

根据瑞雷—里茨能量理论[10]，假设薄板自由振动时的频率为ω及振形为（x，y ），其瞬时挠度可表示为：

由（1）式可得振动速度为：

而对于存在自由边约束的开孔薄板，则由下式计算其应变能：

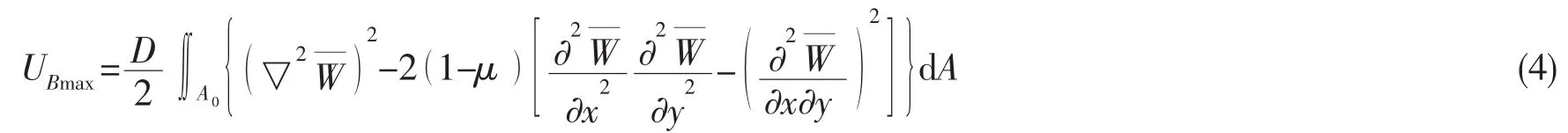
当薄板振动位于其平衡位置时，应变能为零，动能达到最大值KBmax：

其中：称为薄板的弯曲刚度，E为弹性模量，μ为泊松比，A0=A1-A2，A1为整个矩形板的面积，A2为孔口部分的面积，为开孔薄板每单位面积内的质量。

根据能量守恒定理可知，薄板在距平衡位置最远时的应变能需要等于它在平衡位置时的动能。若选定薄板的振形函数（x， ）y 满足位移边界条件，则按（3）至（5）式求出最大应变能及动能，命UBmax=KBmax，即可求得薄板的最低固有频率。

对于用肋条加强了的薄板，仍然可以用能量法求解薄板的固有频率，但须按照肋条的弯曲刚度、质量分布和设定的振形函数求解出肋条的最大应变能ULmax及动能KLmax，并分别计入结构总应变能Umax和总动能Kmax，然后再利用Umax=Kmax计算结构振动频率。

以图1所示加肋板结构为例，肋条在薄板平面内的惯性效应和扭转刚度与其横向抗弯刚度相比可以忽略[11]，因此可以只考虑肋条的横向弯曲振动。同时考虑到肋条的偏心，其刚度的计算以整个薄板横截面的弯曲中性面为参考。

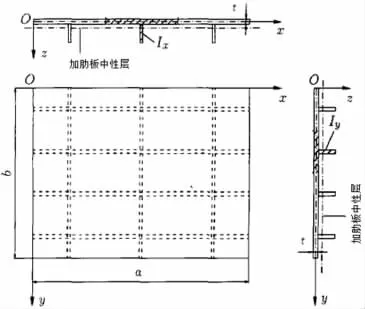
图1 加肋板结构图示Fig.1 Structure of the stiffened plate

x方向某一肋条的应变能和动能可分别表示为

同理y方向某一肋条的应变能和动能可分别表示为

式中：EIy和EIx分别为x、y方向肋条对加肋板中性面的抗弯刚度，x和y分别为x、y方向肋条单位长度上的质量。利用（6）式及（7）式可求出板上肋条的应变能及动能，在此基础上进行叠加即可得到所有肋条的最大应变能ULmax及动能KLmax。在极坐标系下，对（6）式及（7）式做坐标变换即可求解环形加肋的应变能及动能。

对于本文要研究的翻边长圆孔矩形板，由薄板振动理论可知开孔面积及翻边对薄板的固有频率均有影响，下面将利用ANSYS软件分析不同边界条件及翻边长圆孔参数下矩形板的前两阶固有频率，进而分析翻边开孔对其动力性能的影响。

2 翻边开孔模型

定义矩形板开孔率为：

图2 具有翻边长圆孔的矩形板Fig.2 A rectangular plate with circle-rectangular flanged cutout

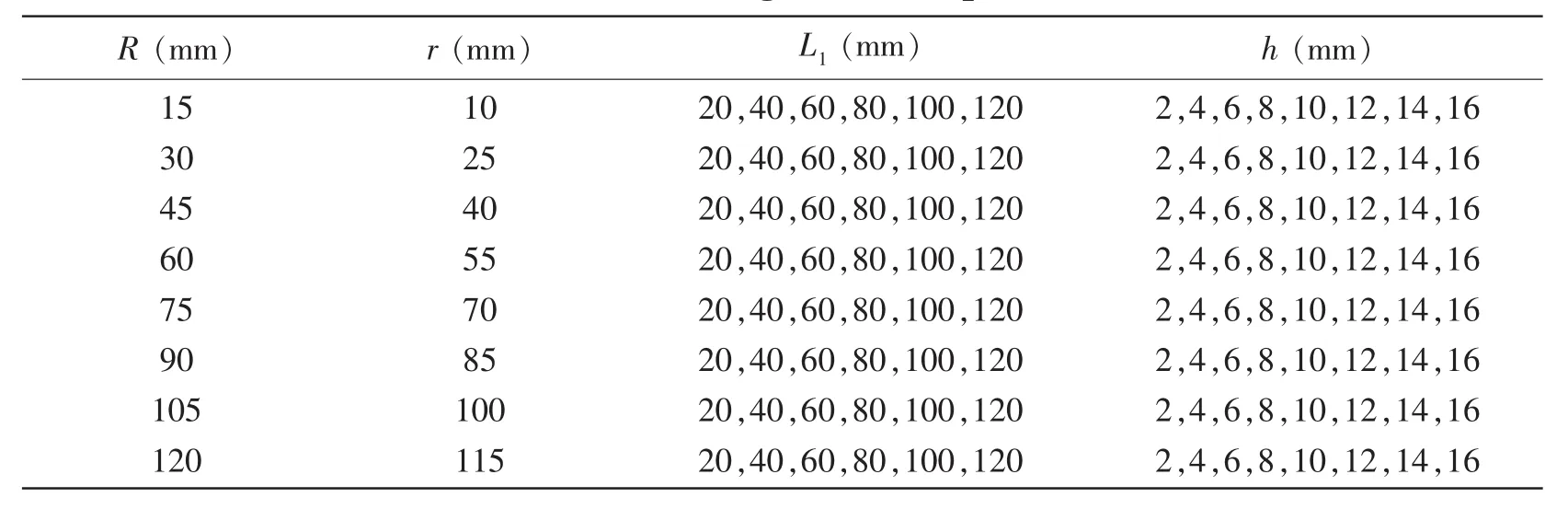
表1 开孔参数的取值Tab.1 Values of flanged-cutout parameters

选取矩形薄板边界条件为固支（Clamped）、简支（Simply supposed）或自由（Free）。做如下规定：从矩形板左边（x=-L/2）边界开始按逆时针顺序，用4个字母分别表示矩形板四个边界的约束条件。利用ANSYS软件APDL程序实现矩形板翻边开孔的参数化建模与分析，选用SHELL181作为模型单元，根据表1中各组开孔参数，对开孔矩形薄板进行振动分析。

3 开孔率对矩形板振动频率的影响

开孔率与大圆半径R及孔直边长度L1有关。首先考虑大圆半径R的影响，在矩形板中心开孔，取直边长度L1=80 mm，翻边高度h=8 mm。表2给出了中心开孔后，一端固支（CFFF）矩形板前两阶固有频率值。为便于比较，对无孔板在一端固支条件下的固有频率进行了模拟，ANSYS分析结果为：f1=8.364 Hz，f2=28.204 Hz。由表2可知：矩形板翻边开孔后，板的固有频率发生了变化，其影响效果与开孔的开孔面积（或开孔率）有关。与未开孔时矩形板的固有频率相比，随着开孔率的增大第一阶频率持续增加；对于第二阶频率，开孔较小时频率不断上升，但随着开孔率的增加而不断降低，而且会出现开孔板的第二阶频率将低于无开孔时板的第二阶频率的情况（φ＞0.023）。

图3给出了其余不同边界约束条件下，矩形板前两阶固有频率随开孔率的变化情况。由图3可知，随着开孔率的增加，这几类边界约束条件下矩形板前两阶频率不断增大，且均大于开孔前板的相应固有频率。翻边开孔对矩形板频率的影响程度与边界条件有关，四边固支（CCCC）条件下的影响程度最高。

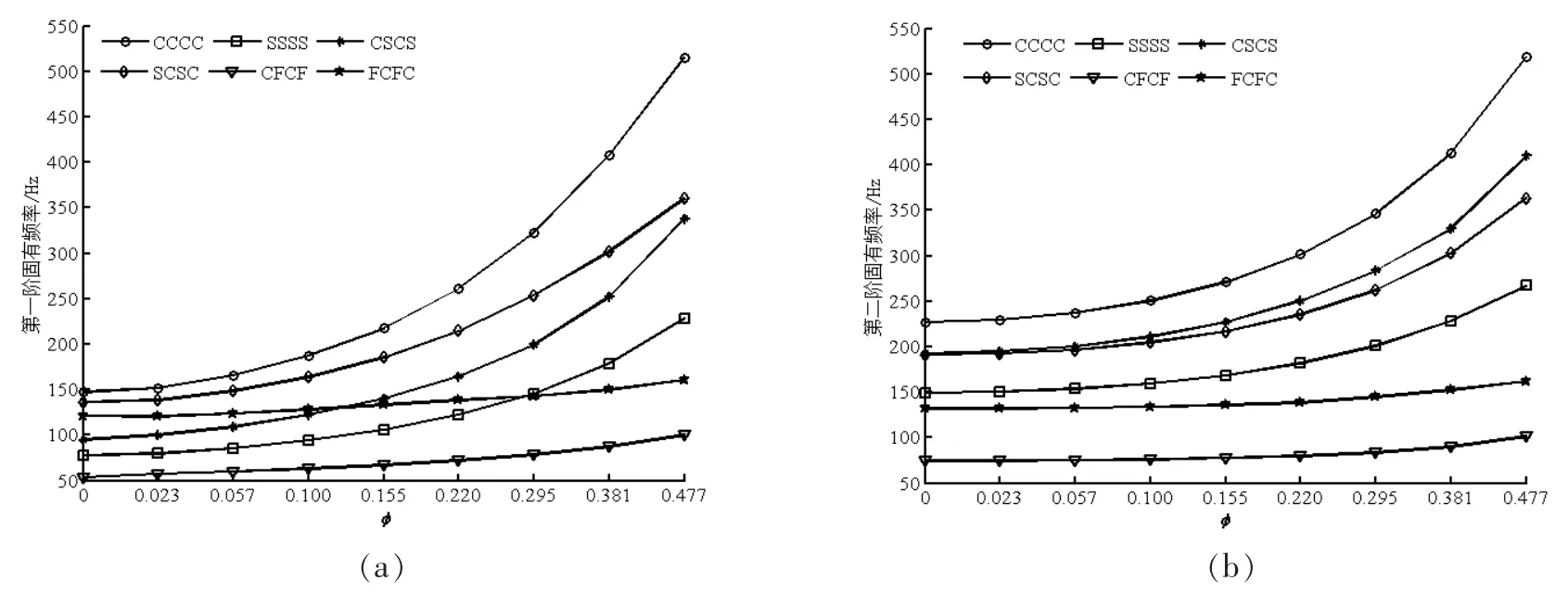
图3 不同约束条件，矩形板前两阶频率随开孔率变化情况 （a）第一阶固有频率；（b）第二阶固有频率Fig.3 Variations of the natural frequeneies of a rectangular plate supposed differently with various area(a)The first natural frequency;(b)The second natural frequency

保持开孔圆尺寸不变和翻边高度不变的情况下，分析直边长度L1对矩形板频率的影响。取R=90 mm，r=85 mm，翻边高度h=8 mm，在矩形板中心开孔。表3给出了一端固支（CFFF）矩形板前两阶固有频率值随L1的变化情况。由表3可知随着直边长度L1的增加，第一阶频率持续增加，均大于未开孔时的频率；第二阶固有频率则不断降低，均小于未开孔时的结果。与表2中所示频率变化趋势一致（φ≥0.023时）。

图4给出了其余几种边界约束条件下矩形板前两阶固有频率随直边长度L1的变化情况。由图4可知，随着直边长度L1的增加，除CSCS约束条件外，这几类边界约束条件下矩形板前两阶频率不断增大，且均大于开孔前板的相应固有频率。而对于CSCS约束条件，第一阶频率随着L1的增加不断升高，第二阶频率呈现先增加后降低的趋势（φ≥0.295）。

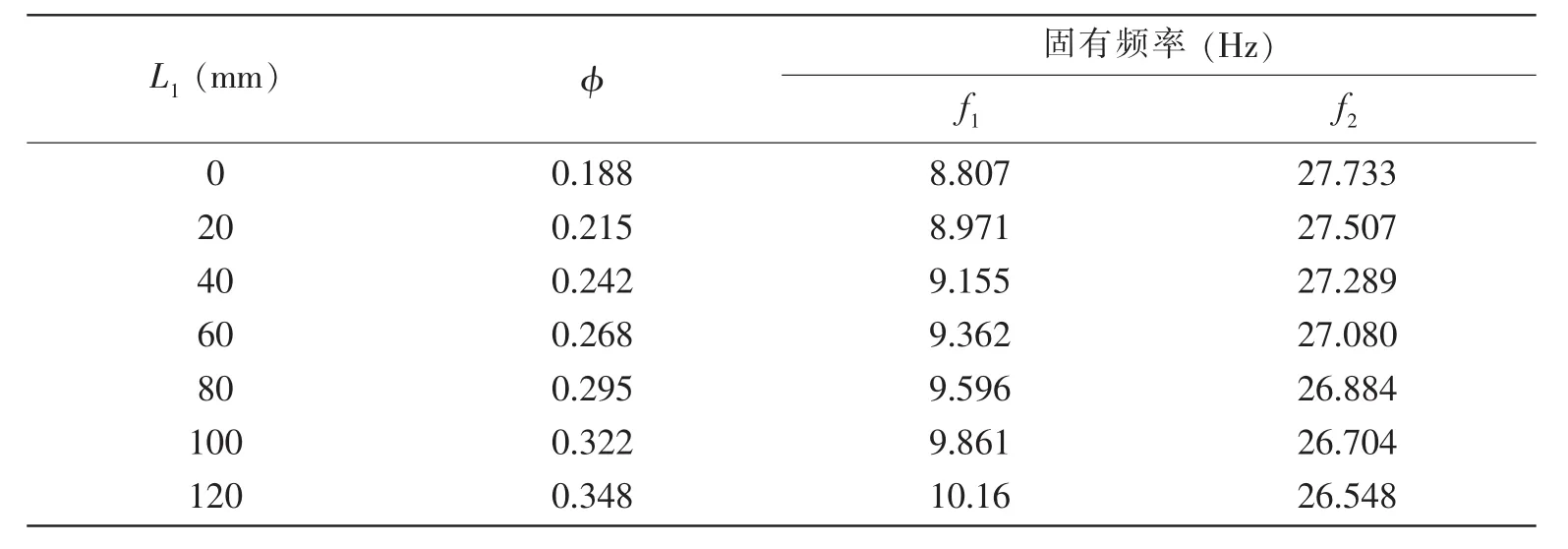
表3 长度L1对一端固支开孔矩形板的频率影响Tab.3 Influence of L1on the first two frequencies of a clamped-free plate

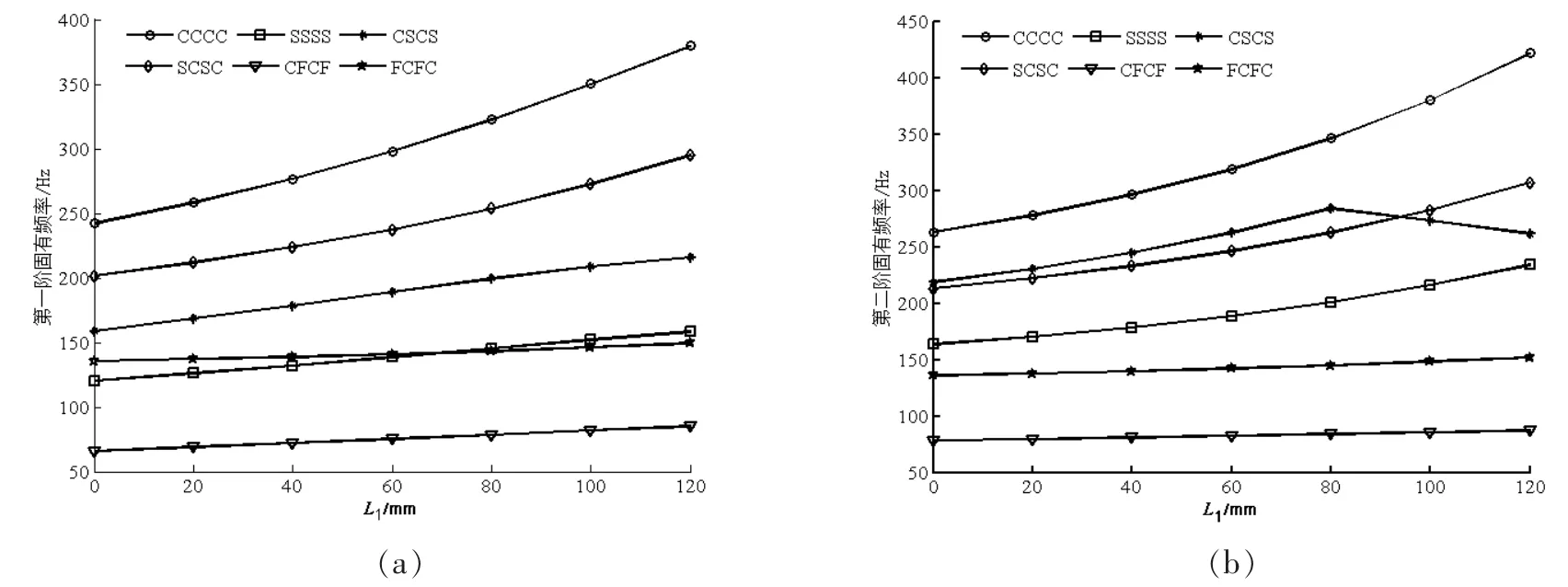
图4 不同约束条件，矩形板频率随直边长度L1变化情况 （a）第一阶固有频率；（b）第二阶固有频率Fig.4 Variations of the natural frequeneies of a rectangular plate supposed differently with various L1(a)The first natural frequency;(b)The second natural frequency

图5给出了CSCS约束条件下开孔矩形板的第二阶振型，表现为反对称于坐标x轴。分析认为在CSCS约束条件下，增大R保持L1不变的开孔方式将结构质量向固支边（矩形板左右两边）集中，增大L1保持R不变的开孔方式则将结构质量向简支边集中，前一种情况下结构的振动频率较大。由此可见开孔形状变化对于矩形板的振动频率也有较大影响。

4 翻边高度对矩形板频率的影响

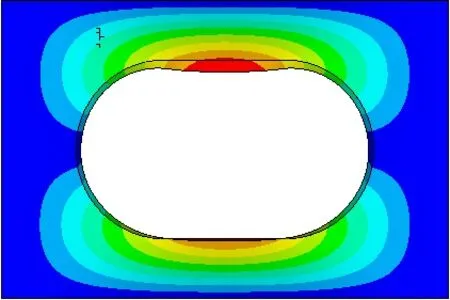
图5 CSCS约束条件下矩形板的第二阶频率振型Fig.5 The second vibration mode of rectangular plate in CSCS

为研究翻边高度对矩形板振动频率的影响，在开孔位置沿图1所示坐标y轴方向截取一矩形板截面，如图6所示。

假设翻边与矩形板平面的夹角为α，当角α发生变化时，翻边开孔矩形板的结构形式及振动频率均会发生变化。由图6可知角α的大小与翻边高度h以及圆半径的差值（R-r）有关，下面分别研究这二者对矩形板振动频率的影响。

首先取 R=90 mm，r=85 mm，L1=80 mm，即开孔率φ=0.295，研究不同翻边高度对矩形板频率的影响。开孔位置依然位于矩形板中心。

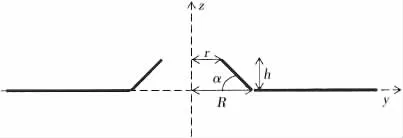
图6 矩形板翻边开孔截面图Fig.6 Section of a rectangular plate with flanged-cutout

表4 翻边高度h对一端固支开孔矩形板前两阶频率值的影响Tab.4 Influence of h on the first two frequencies of a clamped-free plate

表4列出了一端固支矩形板前两阶频率随翻边高度的变化。由表4中数据可知，翻边高度变化对一端固支（CFFF）矩形板频率的影响很大。随着翻边高度的增加，一端固支矩形板前两阶频率值不断增大。与未开孔板的对应频率相比较可以发现当翻边高度较小时，开孔后板的频率值均小于未开孔时的情况。当翻边高度增大到一定情况，开孔后板的频率值则大于未开孔板，如h≥4 mm时，开孔后矩形板第一阶频率值大于相应未开孔情况。对于第二阶频率，则需要翻边高度h≥16 mm。

其余几类约束条件下，翻边高度对矩形板振动频率的影响如图7所示。由图7可知，随着翻边高度h的增加，这几类边界约束条件下矩形板前两阶频率变化总体呈现增大的趋势。与无翻边的开孔板相比，当翻边达到一定高度时，有翻边的开孔板前两阶振动频率均大于无翻边的开孔板。与加肋板类似，这是由于翻边的存在提高了矩形板的面外刚度，而矩形板前两阶振动主要表现为面外振动。同时注意到翻边高度达到一定值时，开孔矩形板频率变化不明显，说明翻边高度对频率的影响程度在降低。

保持开孔率不变（大圆半径R和直边长度L1不变）以及同样翻边高度h的情况下，本文还分析了小圆半径r的变化对矩形板频率的影响。表5给出了开孔率φ=0.295，翻边高度h=8 mm时，小圆半径r变化时一端固支（CFFF）矩形板前两阶固有频率值。由表5可以发现，随着小圆半径r的增加，一端固支矩形板前两阶频率值均不断降低，但第一阶频率均大于未开孔前的相应频率值，当r值达到79 mm时，开孔板的第二阶频率将低于无开孔时板的第二阶频率。

图8给出了其余约束条件下，矩形板前两阶固有频率随小圆半径r的变化情况。由图8可知，随着小圆半径r的增加，这几类边界约束条件下矩形板前两阶频率呈现增大的趋势。开孔后的频率值均大于未开孔矩形板的相应固有频率。当r达到一定值时，矩形板频率变化不明显，小圆半径r对矩形板频率的影响程度在降低。

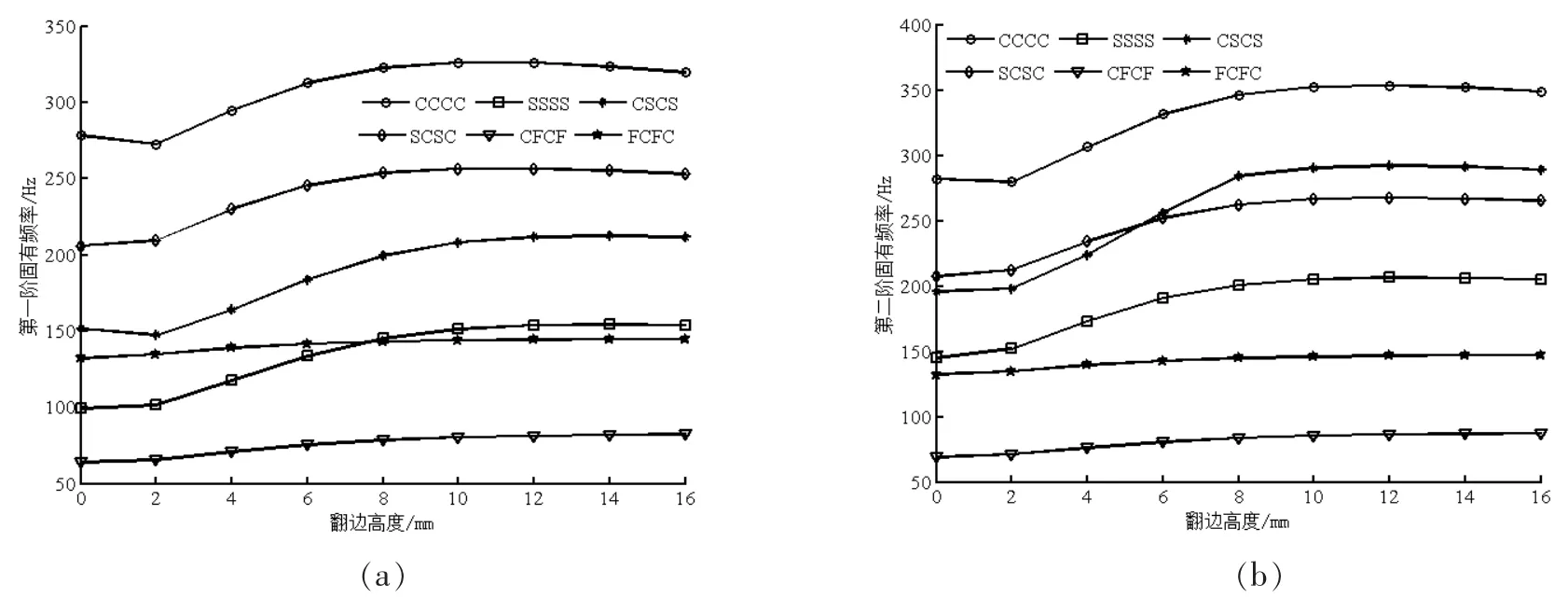
图7 不同约束条件，矩形板频率随翻边高度h变化情况 （a）第一阶固有频率；（b）第二阶固有频率Fig.7 Variations of the natural frequeneies of a rectangular plate supposed differently with various h(a)The first natural frequency;(b)The second natural frequency

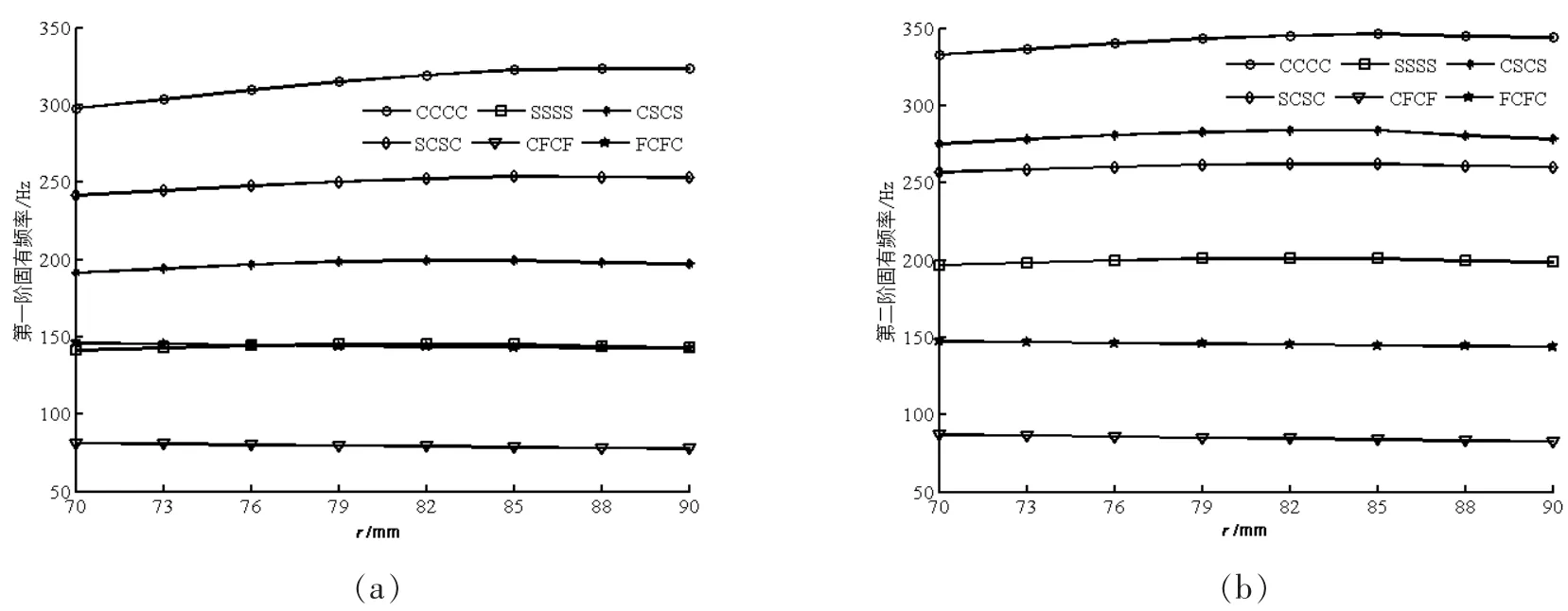
图8 不同约束条件，矩形板频率随小圆半径r变化情况 （a）一阶固有频率；（b）第二阶固有频率Fig.8 Variations of the natural frequeneies of a rectangular plate supposed differently with various r(a)The first natural frequency;(b)The second natural frequency

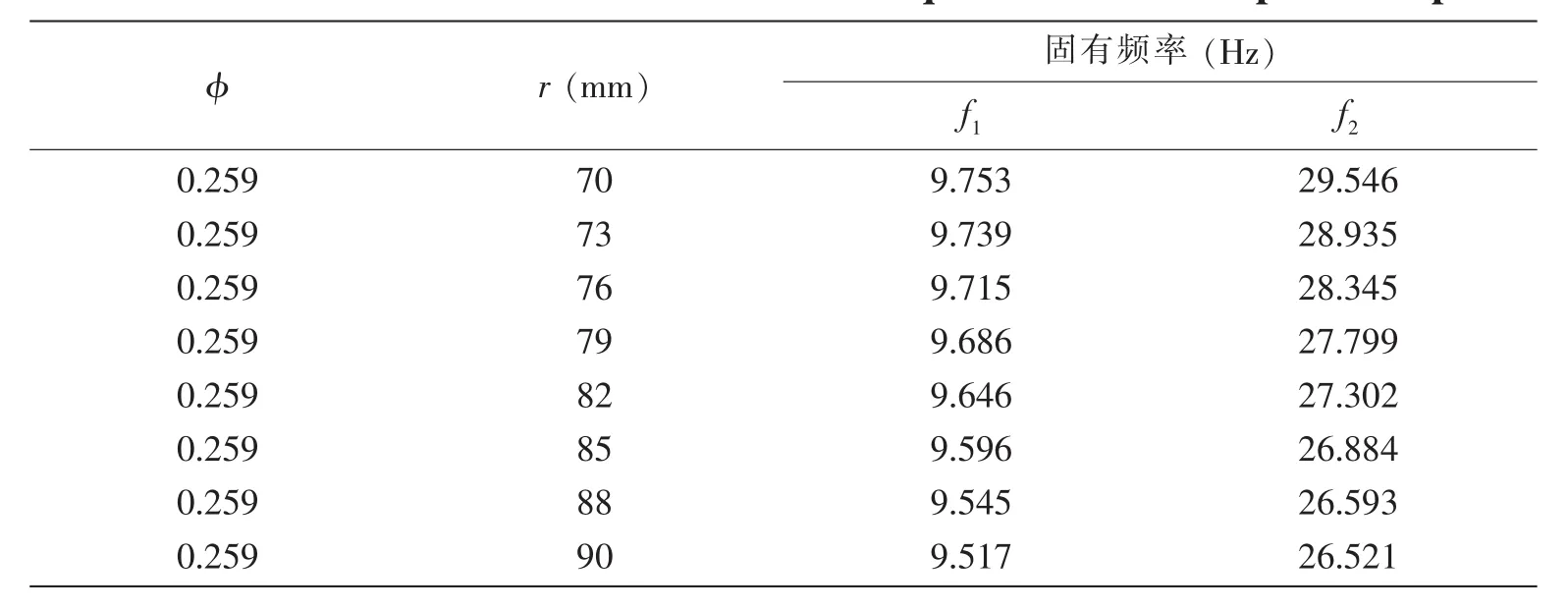
表5 圆半径r对一端固支矩形板前两阶频率值的影响Tab.5 Influence of radius r on the first two frequencies of a clamped-free plate

5 开孔位置变化对矩形板振动频率的影响

取R=90 mm，r=85 mm，L1=80 mm，翻边高度为h=8 mm的开孔矩形板。研究开孔中心位置沿x轴正方向移动时矩形板振动频率的变化情况。

一端固支约束下，矩形板前两阶固有频率随开孔中心位置变化时的结果如表6所示。在同样开孔率的情况下，随着开孔中心位置沿着x轴正方向移动，固支端分布的质量在不断增加，由悬臂结构可知矩形板频率应不断增加，这与表6中所列数据一致。

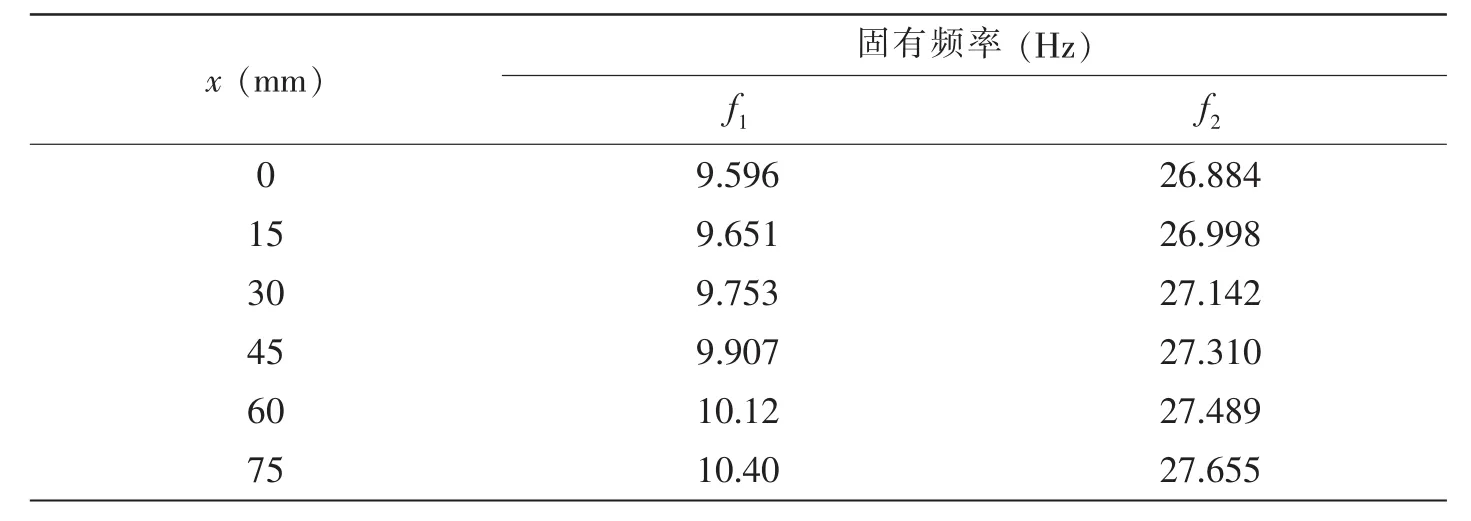
表6 一端固支约束，矩形板前两阶频率值受开孔位置x的影响Tab.6 Influence of x on the first two frequencies of a clamped-free plate

图9给出了其余几种边界约束条件下，开孔矩形板前两阶频率随开孔中心位置的变化情况。由图8可知，随着开孔位置沿x轴正方向移动，开孔后板的第一阶频率呈不断下降趋势。CCCC、SSSS、SCSC这几类边界约束条件下矩形板第二阶频率呈现先增大后减小的趋势，这主要是由于这是因为这几类约束条件下板中心正是第二阶振型的节线位置。对于CSCS、CFCF边界下的矩形板第二阶频率则随着开孔位置沿x轴正方向移动而降低，但变化不明显。而FCFC这类边界条件下矩形板第二阶频率不断增加。

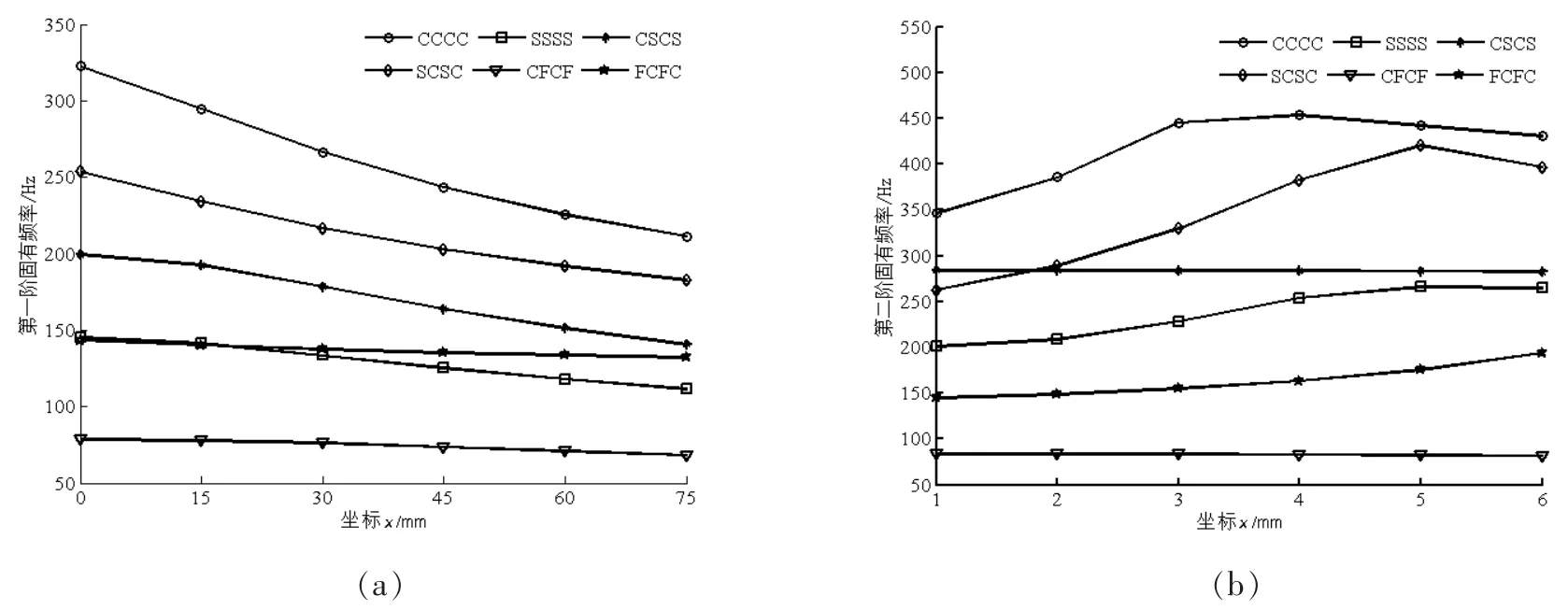
图9 不同约束条件，开孔位置x变化对矩形板频率的影响 （a）第一阶固有频率；（b）第二阶固有频率Fig.9 Variations of the natural frequeneies of a rectangular plate supposed differently with various x(a)The first natural frequency;(b)The second natural frequency

6 翻边长圆孔转动对矩形板振动频率的影响

取R=90 mm，r=85 mm，L1=80 mm，开孔率φ=0.295，翻边高度为h=8 mm的开孔矩形板，研究翻边长圆孔绕开孔中心逆时针转动对矩形板频率的影响。一端固支约束时矩形板前两阶固有频率随开孔转角θ变化结果如表7所示。转角θ的变化对一端固支矩形板前两阶频率的影响效果明显不同，第一阶固有频率在θ=0°时达到最大值，而第二阶固有频率则在θ=45°时达到最大值。

其余几种约束条件时，转动角度变化对矩形板前两阶固有频率的影响如图10所示。对于第一阶振动频率，CCCC和SCSC两类约束条件下频率变化较大，随着角度θ的增加频率呈现下降趋势，其余几类边界条件下一阶频率变化量小，转角的影响非常有限。对于第二阶振动频率，CCCC、SSSS、CSCS和SCSC两类约束条件下频率变化较大，随着角度θ的增加频率呈现下降趋势，其余两类边界条件频率变化受转角的影响小。

表7 转动角度θ对一端固支矩形板前两阶频率值的影响Tab.7 Influence of θ on the first two frequencies of a clamped-free plate with a central circular cutout

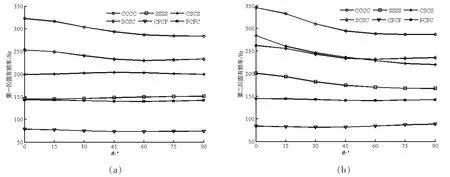
图10 不同约束条件，转动角度θ变化对矩形板频率的影响 （a）第一阶固有频率；（b）第二阶固有频率Fig.10 Variations of the natural frequeneies of a rectangular plate supposed differently with various θ(a)The first natural frequency;(b)The second natural frequency

7 结 论

本文对带有翻边长圆孔的矩形板动力性能进行了研究，分析了开孔率、翻边高度、开孔位置及开孔转动对矩形板振动频率的影响。结果发现：

（1）开孔后矩形板的振动特性变化显著。与无翻边开孔情况相比，翻边的存在增加了矩形板的面外刚度，对其振动性能有较大影响。

（2）不同约束条件下，翻边开孔对矩形板振动频率的影响效果不同。

（3）实际工程结构设计时需根据不同性能要求选择合适的开孔参数。

[1]朱大同.双层开孔板沉箱防波堤的水动力学特征的非线性分析[J].船舶力学,2013,17(1-2):63-74.Zhu Datong.Nonlinear analysis of hydrodynamic behavior for a double-layer perforated-wall caisson breakwater[J].Journal of Ship Mechanics,2013,17(1-2):63-74.

[2]徐海巍,余世策,楼文娟.开孔结构内压传递方程孔口特征参数提取方法研究[J].振动与冲击,2013,32(2):56-61.Xu Haiwei,Yu Shice,Lou Wenjuan.Orifice characteristic parameter identification method for internal pressure transfer equation of opening structures[J].Journal of Vibration and Shock,2013,32(2):56-61.

[3]邱昌贤,万正权,黄进浩.考虑腐蚀减薄的球壳开孔结构随机有限元分析[J].船舶力学,2013,17(11):1269-1277.Qiu Changxian,Wan Zhengquan,Huang Jinhao.Stochastic finite element analysis for spherical shell with round hole in thinned conditions from corrosion[J].Journal of Ship Mechanics,2013,17(11):1269-1277.

[4]董瑞星,陈普会.基于应力约束的翼肋拓扑优化和软件二次开发[J].航空工程进展,2012,3(2):184-188.Dong Ruixing,Chen Puhui.Topology optimization of the wing rib based on stress constrains and software secondary development[J].Advances in Aeronautical Science and Engineering,2012,3(2):184-188.

[5]章泽文.梁腹板开孔加强设计研究[D].上海:上海交通大学,2013.

[6]Peng Hao,Bo Wang,Gang Li,et al.Worst multiple perturbation load approach of stiffened shells with and without cutouts for improved knockdown factors[J].Thin-Walled Structures,2014(82):321-330.

[7]Pedersen N L.Optimization of holes in plates for control of eigenfrequencies[J].Structural and Multidisciplinary Optimization,2004,28(1):1-10.

[8]王 栋,禹志刚.开孔对复合材料层合板振动频率影响研究[J].机械强度,2012,34(5):657-661.Wang Dong,Yu Zhigang.Effect of a cutout within a composite laminated plate on the eigenfrequencies[J].Journal of Mechanical Strength,2012,34(5):657-661.

[9]Huang D T.Effects of constraint,circular cutout and in-plane loading on vibration of rectangular plates[J].International Journal of Mechanical Sciences,2013,68(3):114-124.

[10]徐芝纶.弹性力学[M].北京:高等教育出版社,2008:89-93.Xu Zhilun.Elasticity[M].Beijing:Higher Education Press,2008:89-93.

[11]Prathap G,Varadan T K.Large amplitude flexural vibration of stiffened plates[J].Journal of Sound and Vibration,1978,57(4):583-593.

Influence of flanged-cutout on the natural frequencies of a rectangular plate

WANG Wen-sheng,WEI Hao-jie,HOU Zhong-hua,WANG Zhan-lei,MEI Qun
(Department of Engineering Mechanics,Henan University of Science and Technology,Luoyang 471023,China)

The influence of flanged-cutout on the natural frequencies of a rectangular plate is investigated.A general rectangular plate with circle-rectangular cutout is employed and the ANSYS software is used to evaluate the natural frequencies of the structure.Numerical results show that the frequencies are highly dependent upon the size,flanging height,position and orientation of the cutout,and the effect is also related to the different boundary conditions of the plate.The results can provide references for the design of flangedcutouts in engineering.

flangedge;circle-rectangular cutout;rectangular plate;natural frequencies

O327 TB123

A

10.3969/j.issn.1007-7294.2017.11.010

1007-7294（2017）11-1404-10

2017-04-27

国家自然科学基金资助项目（11402077）；河南科技大学科学研究基金资助项目（13350046）

王文胜（1983-），男，副教授，E-mail：wswang@live.cn；

魏豪杰（1980-），男，博士，讲师。