海流作用下悬浮隧道缆索的运动响应

闫宏生 ， 罗钰淇 ， 余建星

（1.天津大学 水利工程仿真与安全国家重点实验室，天津300072；2.高新船舶与深海开发装备协同创新中心，上海 200240）

海流作用下悬浮隧道缆索的运动响应

闫宏生1，2， 罗钰淇1，2， 余建星1，2

（1.天津大学 水利工程仿真与安全国家重点实验室，天津300072；2.高新船舶与深海开发装备协同创新中心，上海 200240）

考虑参数激励频率，利用涡激振动方程，应用伽辽金和龙格库塔数值积分法，计算出不同流速下参数激励对缆索1阶振动的影响；进一步计算隧道—缆索耦合作用下缆索的振动响应。计算结果表明参数激励为缆索固有频率2倍时，缆索响应最大；隧道对缆索振动有明显的抑制作用。

悬浮隧道；缆索；涡激振动；参数激励

0 引 言

长期以来，如何快速跨越广袤的水域一直是世人关注的焦点。在最近几十年里，一种新的跨越海峡、大江、湖泊、水道的交通结构物—水下悬浮隧道吸引了世人的目光。水下悬浮隧道的研究历史虽然短暂，但由于该种结构的新颖性与其独有的优越性和应用潜力，使得世界各国的学者专家为此进行了很多有价值的工作。近年来，随着对跨越水域的交通通道型式的要求越来越严苛，为了能够更好地适应各种水域地形，对水下悬浮隧道的研究也愈加深入。本文首先对水下悬浮隧道的选型进行了对比分析，综合比较得出了隧道的最佳选型；然后结合算例详细分析了水下悬浮隧道缆索的运动特性，为制定出合理的缆索布置方式提供了可靠的理论依据。

1 悬浮隧道的选型分析

对于横跨水域的交通通道型式，按照空间布局来看，自上而下主要包括：水上桥梁、水下悬浮隧道、海底沉管隧道以及海底深埋隧道等。然而，相比于其他的型式，水下悬浮隧道是迄今为止尚且处在理论分析阶段的前沿技术，目前世界上并没有业已建成或者批准建造的水下悬浮隧道。然而，随着全球经济的快速发展，水下悬浮隧道的技术拥有着广阔的发展前景。

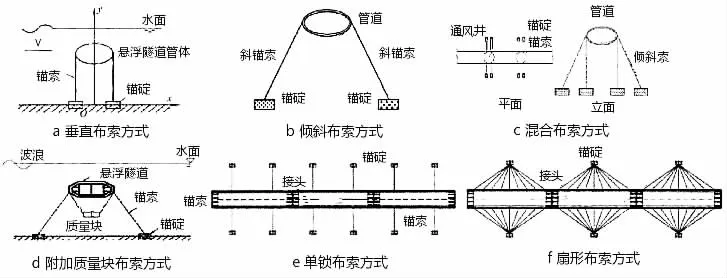
图1 布索方式Fig.1 Cable arrangement

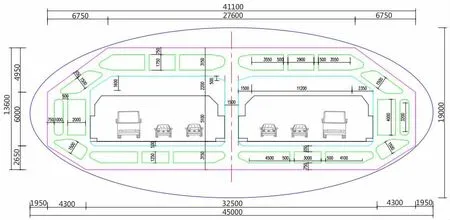
图2 悬浮隧道截面Fig.2 Cross section of submerged floating tunnel

按照锚固形式的不同，水下悬浮隧道可分为锚索式、浮筒式和承压墩柱式，而锚索式水下悬浮隧道是国内外知名科研人员研究的重点。麦继婷等[1]简单研究了水流作用时水下悬浮隧道张力腿在横向发生涡激振动的情况，最后得到了张力腿的动剪力、动弯矩和位移响应同参数激励频率之间的关系；李剑[2]对水下悬浮隧道的锚索发生涡激锁定时的流速进行了初步的探讨；Kanie等[3]对在浮力、倾角和自重不同的情形下水下悬浮隧道张力腿的非线性的恢复力进行了分析计算；葛菲等[4]通过建立波流耦合作用下水下悬浮隧道锚索沿流方向涡激振动的数学模型，探讨了管段运动诱发的参数激励及强迫激励对锚索沿流方向涡激振动的影响。孙胜男等[5]研究了锚索多阶横向振动，建立了锚索—管体耦合振动模型，较为实际模拟了缆索的振动响应。

本文以琼州海峡环境条件为例建设悬浮隧道进行分析。根据文献[6]的研究，目前比较常见的悬浮隧道设计方案有垂直布索、倾斜布索以及混合布索等多种方式，如图1所示。琼州海峡浪高流急，通行船较多，因此锚索式悬浮隧道成为较好的选择。同时，由于海底地形复杂，海流速度较快，悬浮隧道需要较大的水平约束。倾斜的锚索可提供水平和竖直两个方向的分力，竖直分力抵抗浮力，水平分力抵抗环境作用产生的水平力，单索的的布置也能保证隧道的稳定性。因此，本文推荐采用倾斜布索式悬浮隧道。隧道截面尺寸如图2所示。图3为六车道悬浮隧道示意图。

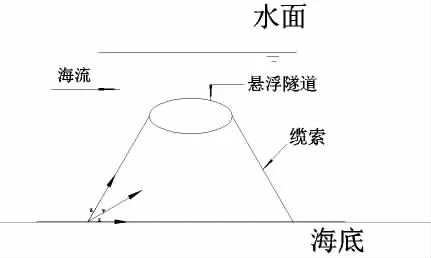
图3 六车道悬浮隧道图示Fig.3 Schematic diagram of submerged tunnel

2 悬浮隧道缆索的运动特性分析

悬浮隧道缆索类似于张紧式的张力腿形式，因此可将其简化为简支梁。选取跨中为参考点。首先对缆索计算分析作如下假设：

（1）缆索张力远小于重力，因此忽略张力沿长度方向的变化，即缆索拉力各处相等；

（2）缆索的材料属性、刚度和几何特性沿长度不发生变化；

（3）海流为线性流，海底流速为零；

（4）z轴是锚索轴向方向，y轴为隧道方向，x轴为海底方向，来流方向为x轴正方向；（5）只考虑缆索的横向振动，即y-z平面内的振动。

2.1 悬浮隧道管段对缆索运动影响分析

根据文献[7]的研究，可将悬浮隧道的影响简化为参数激励，缆索的横向振动方程为：

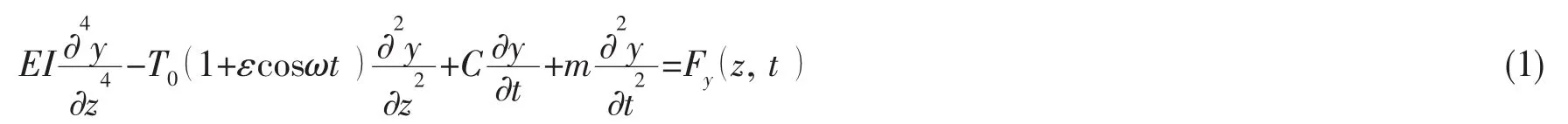
式中：T0为静张力，ε为动静张力比，ω为参数激励频率；Fy（z,t）=Fl-Fd；Fl为涡激振动产生的升力：

式中：ρ为海水密度，；D为缆索直径，CL为升力系数，取0.6，v为流速；θ为缆索的倾角；ωv为涡街泄放频率。

Fd为横向振动引起的单位长度水体阻尼力和附加质量力[7]：

式中：CD为拖曳力系数，取0.7；Cm为附加质量系数，取1.0。

用分离变量法将锚索横向振动Fy（z,t）化为简支梁固有振型级数形式为：

将（2）、（3）式和（4）式代入（1）式，整理得：

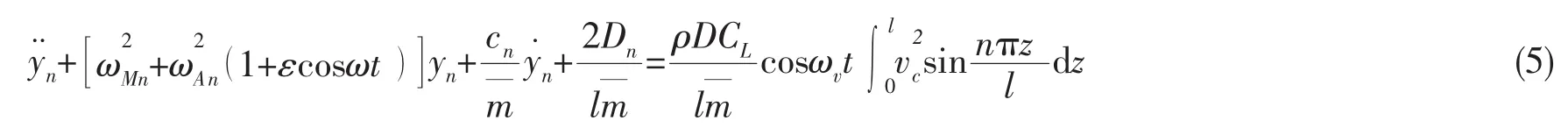
2.2 缆索—隧道耦合非线性振动

在实际工程中，由于水下复杂的海流环境，缆索作为悬浮隧道重要的结构，模拟计算时要尽量准确。悬浮隧道对缆索横向振动并不仅限于参数激励，上述模型并不能完全反应缆索振动实际情况，因此，建立缆索—隧道耦合振动模型，更能反应在实际海况下缆索的横向振动响应。

缆索—隧道耦合模型[5]，将隧道简化为有刚度，阻尼的质量块，振动方向为z方向。如图4所示。在上述假定下，缆索的振动微分方程为

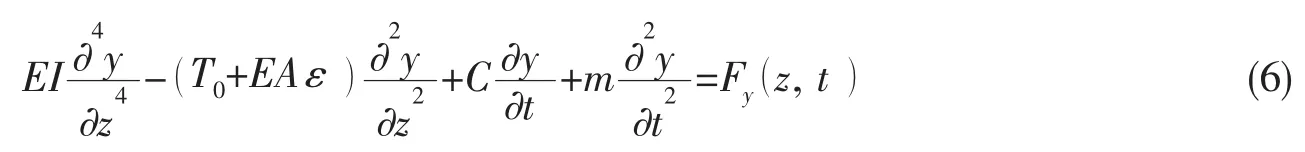
悬浮隧道振动微分方程：

缆索的动应变：

将（8）式代入（6）、（7）式用伽辽金法化简整理，得：

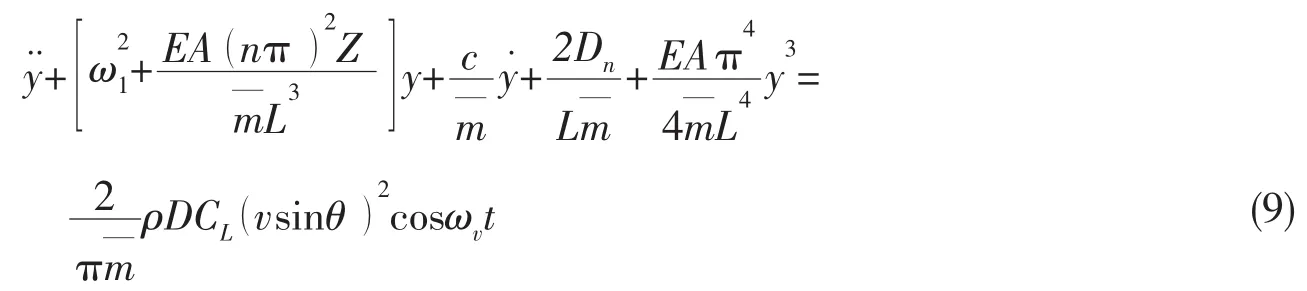
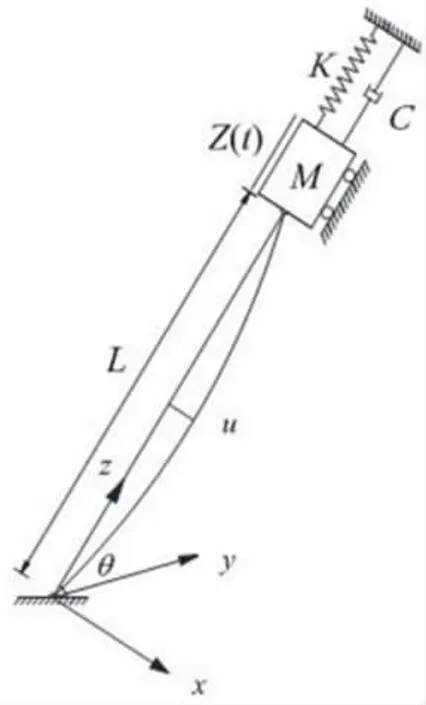
图4 缆索—隧道耦合模型示意图Fig.4 Schematic diagram of coupled vibration model of cable-tunnel

管段的振动方程整理得：

式中：ωM为单节悬浮隧道的固有频率，ξM为隧道阻尼比。

则缆索与管段耦合振动方程组为：

（11）式将（1）式中的参数激励ε表达为由隧道振动引起缆索刚度的变化，方程组的联立将悬浮隧道运动与缆索的运动耦合考虑，更符合实际情况。

将悬浮隧道对缆索激励简化为参数激励频率的模型，能显著体现涡激振动和参数振动振动规律；隧道—缆索耦合模型更符合实际情况，计算结果较为精确。

3 算例分析

计算数据取：水深100 m，隧道深度40 m，悬浮隧道截面为椭圆，长轴45 m，短轴18 m，单节隧道长100 m，斜布5对缆索，缆索长度69.2 m，缆索与海底夹角60°，一阶固有频率与静张力T0相关，即不同流速下固有频率不同；动静张力比ε=0.432，＝1 037.4 kg/m，EI=4.998 7e+05 kN·m2。

3.1 不考虑隧道对缆索影响

根据理论知识，1阶谐振对缆索影响较大。因此，本文分析在不同流速情况下参数激励的变化对缆索 1 阶振动的影响。图（a）、（b）、（c）和（d）分别表示参数激励为：（a） ω=0；（b） ω=ω1；（c） ω=2ω1；（d） ω=3ω1。

图5 1m/s流速下不同参数激励对缆索一阶振动位移响应Fig.5 The first-order displacement response in different parametric excitation at 1 m/s current velocity

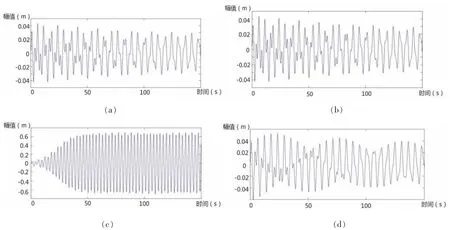
图6 2m/s流速下不同参数激励对缆索一阶振动位移响应Fig.6 The first-order displacement response in different parametric excitation at 2 m/s current velocity

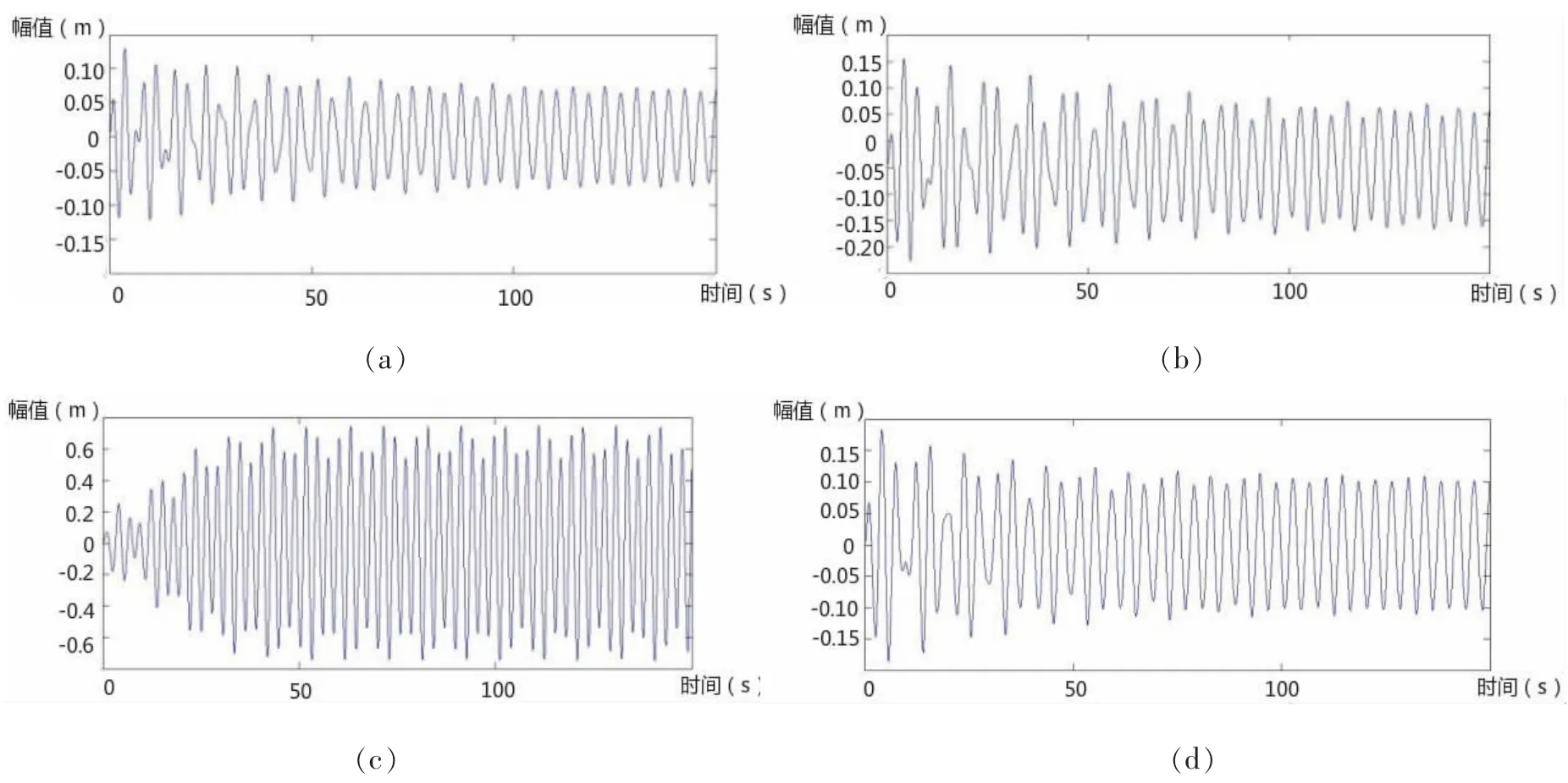
图7 3m/s流速下不同参数激励对缆索一阶振动位移响应Fig.7 The first-order displacement response in different parametric excitation at 3 m/s current velocity

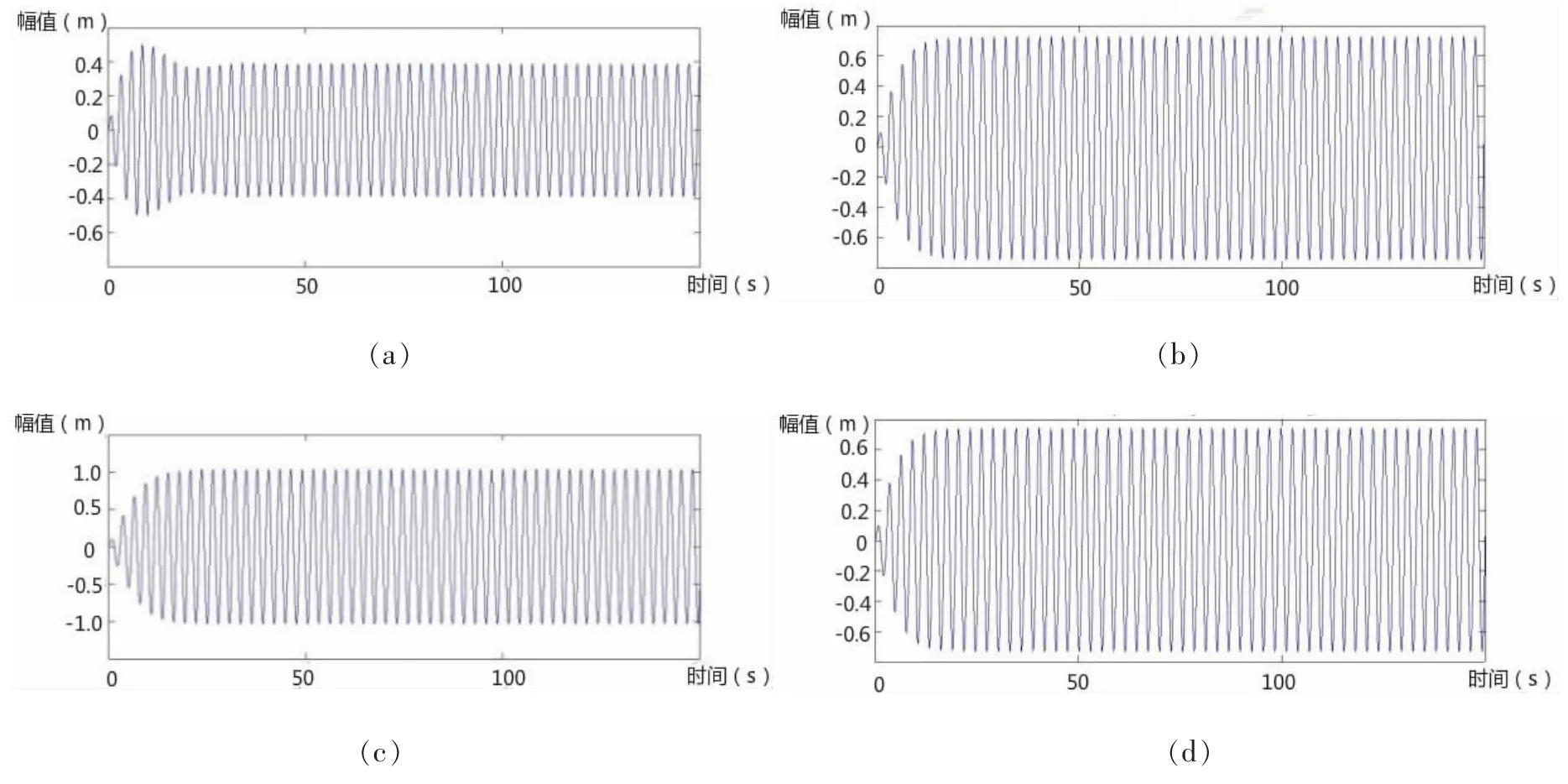
图8 4.2m/s流速下不同参数激励对缆索一阶振动位移响应Fig.8 The first-order displacement response in different parametric excitation at 4.2 m/s current velocity

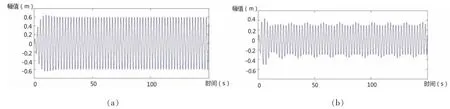
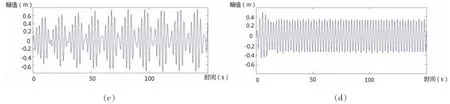
图9 5m/s流速下不同参数激励对缆索一阶振动位移响应Fig.9 The first-order displacement response in different parametric excitation at 5 m/s current velocity

从上述各图中可以看出，总体上缆索的振动随着流速的增大而增大，但图6缆索振动明显增大；各组图中只有当参数激励频率等于2倍缆索1阶固有频率时，振动幅值最大，其余情况缆索振动并无明显变化。

计算结果表明，在不计缆索几何形变，刚度差异和材料属性的条件下，缆索振动幅值随流速增大而增大，流速达到4.2 m/s时，涡街泄放频率与缆索1阶固有频率相同，发生了谐振，导致振动幅值明显增大。参数激励为缆索固有频率的2倍时，同样发生谐振，图4（c）中缆索既发生了涡激谐振，又同时发生参数谐振，缆索振幅达到最大1.1 m。从整体上来说参数振动的影响大于涡激振动的影响。

3.2 缆索—悬浮隧道耦合非线性振动

悬浮隧道的固有频率对缆索有很大影响，根据上文结果，分别计算管段的固有频率：（a）ωM=ω1，（b）ωM=2ω1两种情况下缆索振动幅值。假定管段质量不变，通过改变刚度调整ωM。

从图中可以看出，缆索振幅依旧随流速增大而增大，在4.2 m/s流速下，缆索发生涡激谐振；在各流速下，当ωM=2ω1时依然达到最大振幅，说明在管段固有频率等于缆索固有频率2倍时发生谐振。总体上看当悬浮隧道与缆索耦合作用时，隧道大幅抑制了缆索的振动，涡激振动和参数激励振动仍是引起缆索振动的主要因素。

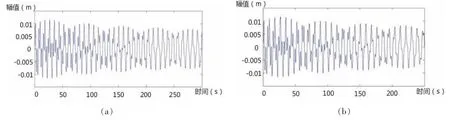
图10 1m/s流速下缆索—悬浮隧道耦合作用缆索的位移响应Fig.10 The displacement response of cable with coupled model at 1 m/s current velocity

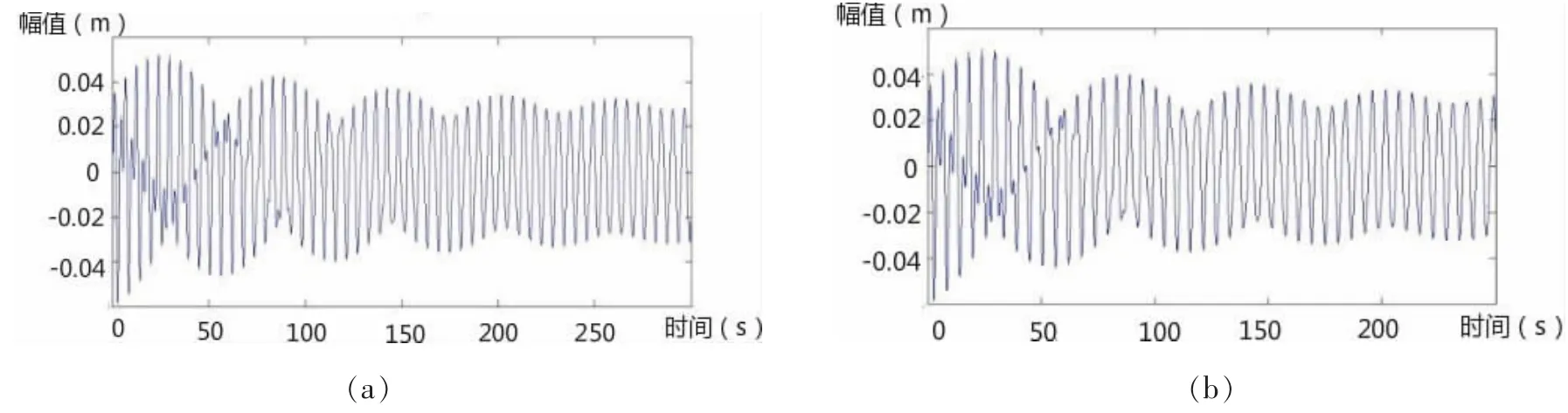
图11 2m/s流速下缆索—悬浮隧道耦合作用缆索的位移响应Fig.11 The displacement response of cable with coupled model at 2 m/s current velocity

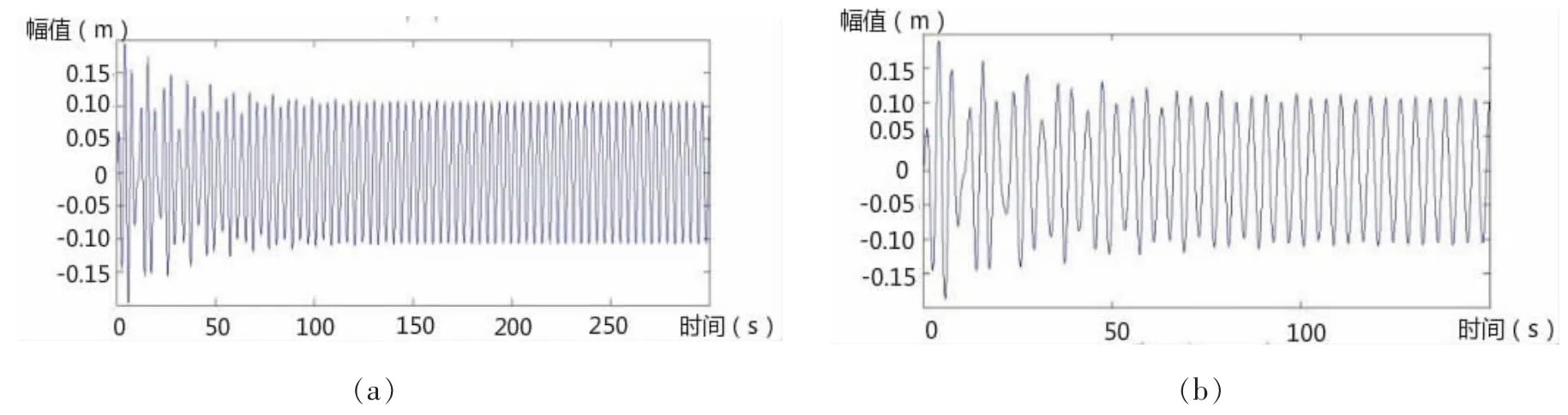
图12 3m/s流速下缆索—悬浮隧道耦合作用缆索的位移响应Fig.12 The displacement response of cable with coupled model at 3 m/s current velocity

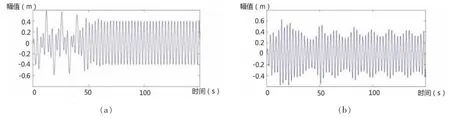
图13 4.2m/s流速下缆索—悬浮隧道耦合作用缆索的位移响应Fig.13 The displacement response of cable with coupled model at 4.2 m/s current velocity

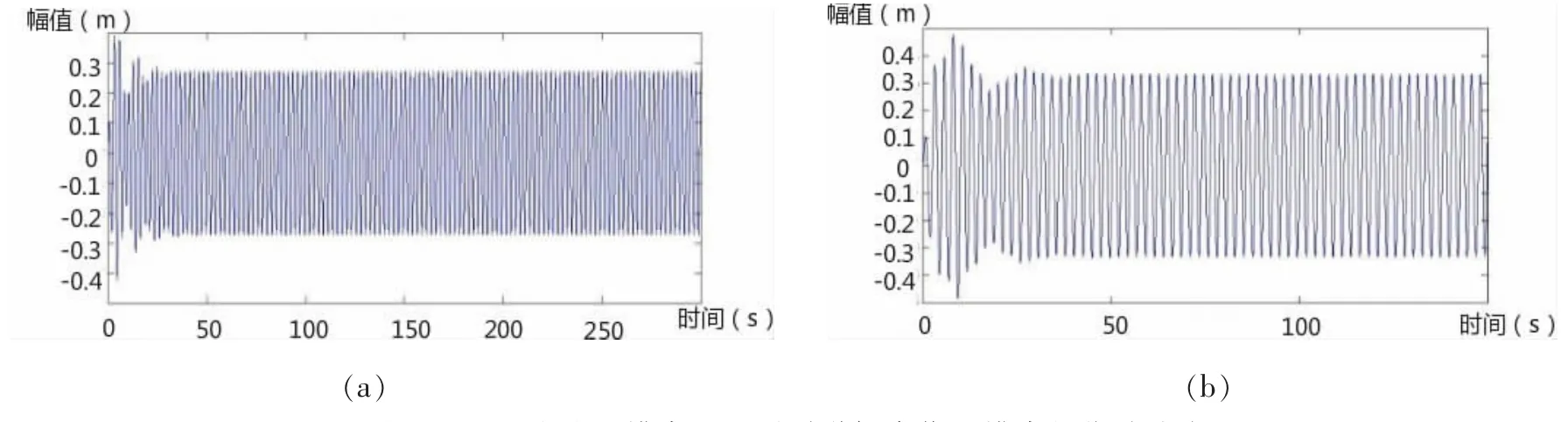
图14 5m/s流速下缆索—悬浮隧道耦合作用缆索的位移响应Fig.14 The displacement response of cable with coupled model at 5 m/s current velocity

4 结 论

本文利用缆索的涡激振动方程，对悬浮隧道缆索进行响应分析，讨论了参数激励的影响，管段非耦合与耦合对缆索的影响，可以得到以下结论：

（1）涡激振动和参数激励振动是缆索振动的主要因素，其中参数激励振动为主导；

（2）参数激励为缆索固有频率2倍时，位移响应最大；

（3）管段对缆索振动有明显的抑制作用，但当发生涡激谐振和参数激励谐振时，缆索的位移响应仍然较大。

（4）由于目前并无已建成的悬浮隧道，前期悬浮隧道具体参数没有确定，导致缆索的实际振动与模拟数值有所偏差。

缆索作为悬浮隧道固定结构，在海流作用下发生振动，其疲劳问题必须考虑。本文可为后续研究缆索的动力响应、疲劳问题打下基础。

[1]麦继婷,罗忠贤.流作用下悬浮隧道张力腿的涡激动力响应[J].西南交通大学学报,2004,39(5):600―604.Mai Jiting,Luo Zhongxian.Vortex induced dynamic response of tension leg of suspension tunnel under flow[J].Journal of Southwest Jiaotong University,2004,39(5):600―604.

[2]李 剑.水中悬浮隧道概念设计及其关键技术研究[D].上海:同济大学,2003.Li Jian.Conceptual design and key technologies of submerged floating tunnels[D].Shanghai:Tongji University,2003.

[3]Kanie S,Mikami T,Horiguchi H.Effect of non-linearity in restoring force on dynamic response of SFT[C].Krobeborg.Strait Crossing 2001.Swetsamp;Zeitlinger Publishers Lisse,2001:529―534.

[4]葛 斐,董满生,惠 磊,洪友士.水中悬浮隧道锚索在波流场中的涡激动力响应[J].工程力学,2006,23(S1):217―221.Ge Fei,Dong Mansheng,Hui Lei,Hong Youshi.Vortex excited response of submerged floating tunnel anchor in wave field[J].Engineering Mechanics,2006,23(S1):217―221．

[5]孙胜男．悬浮隧道动力响应分析[D]．大连:大连理工大学,2008.Sun Shengnan．Dynamic response analysis of suspension tunnel[D]．Dalian:Dalian University of Technology,2008．

[6]闫宏生,杨国彬,余建星．水下悬浮隧道选型研究[J].施工技术,2015,44(7):113-116.Yan Hongsheng,Yang Guobin,Yu Jianxing,The lectotype study on the submerged floating tunnel[J].Construction Technology,2015,44(7):113-116．

[7]唐友刚．高等结构动力学[M].天津:天津大学出版社,2012:210-219.Tang Yougang.Advanced structural dynamics[M].Tianjin:Tianjin University Press,2012:210-219.

Dynamics response of cables for SFT under current effect

YAN Hong-sheng1,2,LUO Yu-qi1,2,YU Jian-xing1,2
(1.State Key Laboratory of Hydraulic Engineering Simulation and Safety,Tianjin University,Tianjin 300072,China;2.Collaborative Innovation Center for Advanced Ship and Deep-sea Exploration,Shanghai 200240,China)

Based on the equations of vortex-induced vibration,the effect of parametric excitation frequency on the first-order response of cable at different velocity of current is analyzed by considering the parametric excitation.In the analysis,the Galerkin method and the Runge-kutta numerical integration are used.In the further analysis,vibration of anchor cable is calculated with model of coupled cable-tunnel.The result shows that when the frequency of parametric excitation twice as the first-order natural frequency of cable,the displacement response is the largest.The displacement of cable is limited by submerged floating tunnel obviously.

submerged floating tunnel;cables;vortex-induced vibration;parametric excitation

U459.5

A

10.3969/j.issn.1007-7294.2017.11.005

1007-7294（2017）11-1356-09

2017-05-17基金项目：高新船舶开发装备协同创新中心，水利工程仿真与安全国家重点实验室联合资助

闫宏生（1973-），男，博士，副教授；

罗钰淇（1993-），男，硕士研究生；

余建星（1958-），男，博士生导师，973首席科学家。