环状粘弹层合悬臂薄壁圆柱壳的振动特性研究

王 宇，翟敬宇，李 昌，宋 华

（1.辽宁科技大学 机械工程学院，辽宁 鞍山 114051；2.大连理工大学 机械工程学院，辽宁 大连 116024）

环状粘弹层合悬臂薄壁圆柱壳的振动特性研究

王 宇1，翟敬宇2，李 昌1，宋 华1

（1.辽宁科技大学 机械工程学院，辽宁 鞍山 114051；2.大连理工大学 机械工程学院，辽宁 大连 116024）

文章采用传递矩阵法分析了悬臂边界条件下环状局部覆盖粘弹层合薄壁圆柱壳的振动特性。基于乐甫薄壳理论，结合粘弹性阻尼的变形协调关系和层间作用力关系，建立了基层和约束层薄壁圆柱壳的一阶状态微分方程，利用传递矩阵法推导了结构的整体传递矩阵，并通过高精度的精细积分方法进行求解，得到了固有频率、损耗因子和三维振型，探讨了约束阻尼层位置变化时对振动特性的影响，并通过有限元法进行了比较，通过算例验证了传递矩阵法对模态特性分析的有效性，前25阶模态以周向振动为主，最低阶固有频率对应的三维模态振型为(1，5)，并且在悬臂端的振动位移最大，约束阻尼层覆盖位置对薄壁圆柱壳振动特性的影响较大。

粘弹层合薄壁圆柱壳；悬臂边界条件；环状覆盖；三维振型

0 引 言

薄壁圆柱壳构件在船舶、潜艇和航空航天等机械领域中应用广泛，在外部复杂载荷等实际工况条件下，容易发生共振、失稳和疲劳损伤等故障，在服役过程通常使用敷设阻尼层对其进行减振降噪处理，由于实际管系布置和结构优化等因素，有时采用局部覆盖约束阻尼层的方式，近年来其振动控制一直是研究的热点问题之一[1-2]。对于悬臂边界条件（即固支—自由约束条件）的薄壁圆柱壳构件，在基频激励作用下，作者对发生共振时的振动响应特征进行了研究，说明了对壳体结构进行模态振型、模态数量和振动特征分析的关联和重要性[3-4]。然而，在悬臂边界条件下，对带有局部覆盖粘弹层合薄壁圆柱壳的高阶振动问题，例如约束阻尼层位于壳体不同位置时的三维模态振型等方面，尚缺少相应的研究成果，因此，对其振动特性进行深入研究，具有重要的理论意义和工程应用价值[5-8]。

利用粘弹性材料的高阻尼性能对薄壁圆柱壳构件进行振动抑制处理，改善薄壁圆柱壳构件的动力学性能，很多学者进行了这一领域的研究，并取得了众多成果，具有代表性的文献如下：Wang和Chen[9]利用模态假设法研究了局部覆盖约束阻尼层圆柱壳的动力学问题，结果表明结构阻尼随着约束层厚度和刚度的增大而增加，当约束层厚度达到一定值时阻尼效果并不明显。Chen和Huang[10-11]研究了固定大小的带状被动约束阻尼层个数对圆柱壳振动衰减的影响。Sainsbury[12]和Mastib[13]采用有限元法研究了部分覆盖约束阻尼层圆柱壳应变能强度的分布规律和减振方法。Mohammadi等[14]根据粘弹性层厚度方向上的位移变化关系，推导了约束阻尼层合壳的有限元模型，研究得到了其振动特性。李恩奇等[15]基于唐奈尔薄壳理论和哈密顿原理，推导出局部覆盖约束层阻尼圆柱壳的运动方程，并通过Laplace变换和传递函数法得到了对边固支边界条件下的固有频率、损耗因子和频响曲线。杨少红和王安稳[16]应用混合分层理论，推导出两端简支粘弹性层合圆柱壳的动力学方程，得到了结构的振动频率和损耗因子。王祖华等[17]利用模态展开和Green函数法，分析了两端简支边界条件下敷设阻尼层环肋圆柱壳在流场中的声辐射特性。曹雄涛等[18]利用桑德斯薄壳理论和波传播法，求解了两端简支被动约束层阻尼圆柱壳的自由振动特性。李超等[19]建立了圆柱壳阻尼材料的优化模型，对约束阻尼和自由阻尼材料布局进行了优化研究。王淼等[20]基于哈密顿变分原理，获得了悬臂夹层圆柱壳的运动微分方程，采用谱有限元法研究了长径比和径厚比对固有频率和损耗因子的影响。

本文针对悬臂边界条件下的环状局部覆盖粘弹层合薄壁圆柱壳，基于薄壳理论和粘弹性理论，采用传递矩阵法进行了振动特性研究，求解得到了结构的高阶固有频率、三维模态振型和模态损耗因子，并通过有限元方法进行了比较，最后分析了约束阻尼层位置对整体结构振动特性的影响。

1 整体结构的模态特性分析

1.1 环状覆盖粘弹层合悬臂薄壁圆柱壳模型

如图1所示为局部环状覆盖粘弹性层合悬臂薄壁圆柱壳的模型，在柱坐标系Oxθz中，基层长度、中面半径和壁厚表示为L、R1和H1，粘弹性阻尼层和约束层的长度均为L2-L1，阻尼层的中面半径和壁厚表示为R2和H2，约束层的中面半径和和厚度表示为R3和H3，uj、vj和wj表示基层和约束层在x、y和z方向上的振动位移。

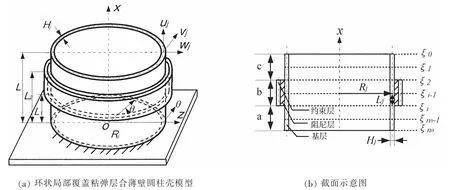
图1 局部覆盖粘弹层合悬臂薄壁圆柱壳模型Fig.1 Model of a partially covered viscoelastic laminated cantilever cylindrical shell

1.2 变形协调关系和层间作用力

粘弹性阻尼层通过基层和约束层的弯曲变形，起到振动耗能减振，由基尔霍夫平面假定和乐甫壳体理论[21]，假设分别表示基层和约束层的中面沿x、θ和z方向上的振动位移，阻尼层内沿x和θ方向的剪应力为：

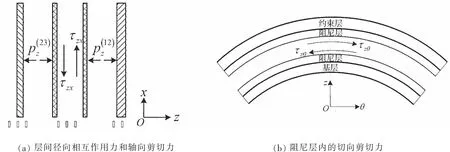
图2 层间径向相互作用力和阻尼层内的剪切力Fig.2 Radial interactions between layers and shear force in damping layer

如图2所示，对于粘弹阻尼层，当仅考虑法向惯性力时的平衡方程为

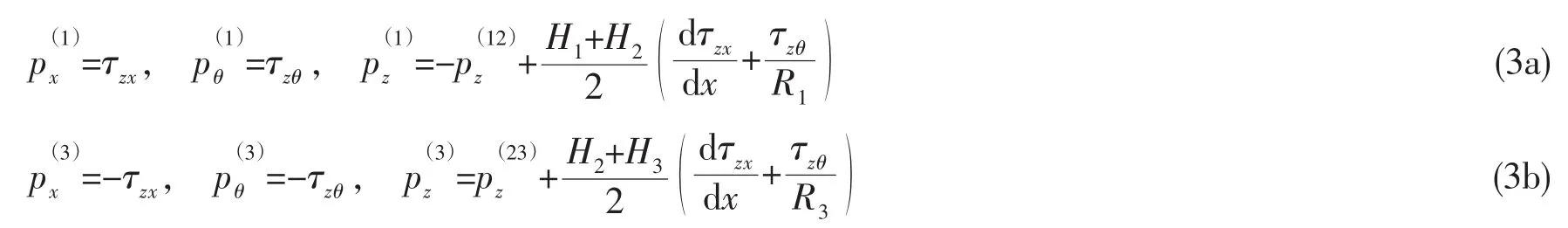
1.3 振动特性求解

首先，对基层（即j=1）进行分析，忽略任一区段的下角标i，振动微分方程表示为

内力与内力矩和中面位移间的关系为：

式中：E1为杨氏模量，μ1为泊松比，K1为薄膜刚度，D1为弯曲刚度。

对于面内剪力、横向剪力和中法线绕θ轴的转角，表达式分别为：

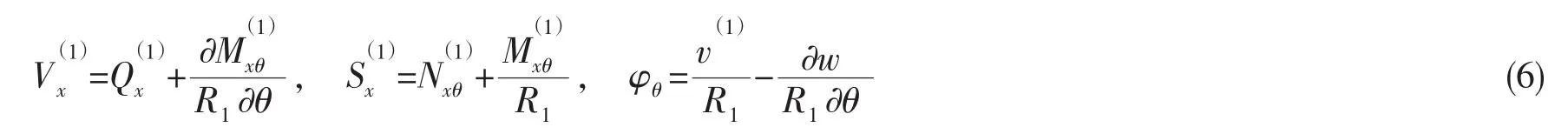
令m表示轴向半波数，n表示周向波数，ωmn表示固有频率，定义位移解的形式为：

定义任一截面ξi上状态向量中的8个元素为：

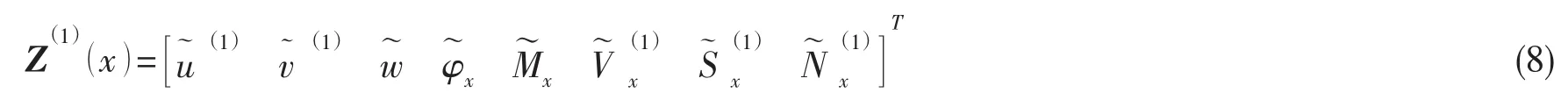
则位移、转角、内力和内力矩表示为：

整理得到一阶状态向量微分方程组为：

同理，对于约束层薄壁圆柱壳，任一截面上状态向量为：

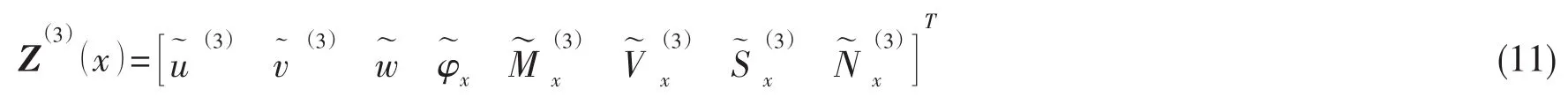
一阶状态向量微分方程组表示为：

对于基层和约束层，传递矩阵的关系为：

消除变量后，定义状态向量中的12个元素为：

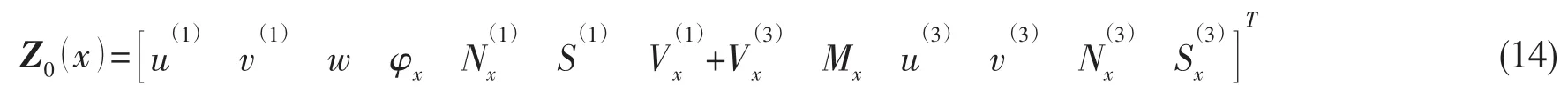
将变形协调关系式（1）和法向平衡方程式（2），代入基层与约束层的振动微分方程中，对变量进行整理，推导得到一阶微分方程组为：

式中：U是12×12阶的矩阵。

如图1所示，对整体结构进行求解时，可沿纵向分成a、b、c三段，将状态向量式（14）进行处理，令

对于a段和b段的薄壁圆柱壳采用（10）式和（12）式描述，对于覆盖区域采用（14）式描述。在轴向截面x=0、L1、L2和L位置，状态向量之间存在关系为：

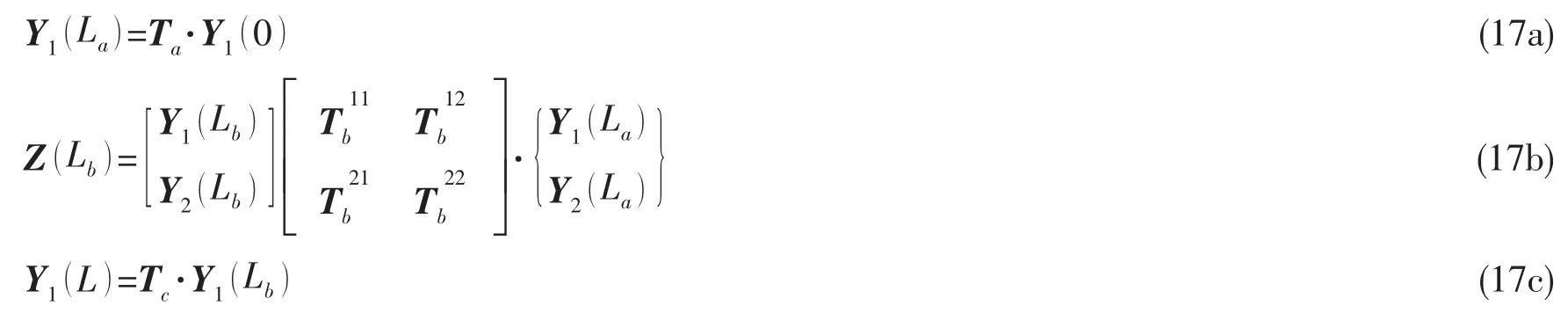
式中：Ta、Tb和 Tc分别为 a、b和 c段的传递矩阵。

消去 Y1（La）和 Y1（Lb），整理得

对于某一阶模态，整合各个变量后可以得到ξ0层的径向位移，然后利用每个区段的子传递矩阵关系，可以得到任一截面处的振动位移关系，最后求出整体结构的模态振型。

则固有频率和模态损耗因子分别为：

2 算例求解与分析

在悬臂边界条件下，通过算例对模态特性进行求解，选取构件的几何参数与材料参数为：L=0.3 m，L1=0.1m，L2=0.2 m，R1=0.3 m，H1=0.003 m，H2=0.001 m，H3=0.002 m，基层和约束层的弹性模量为 E1=E3=70 GPa，密度为 ρ1=ρ3=2 700 kg/m3，泊松比为 μ1=μ3=0.3，粘弹性层的复剪切模量为 G2=0.896泊松比 μ2=0.498，ρ2=999 kg/m3。

（1）中部覆盖阻尼层薄壁圆柱壳的振动特性

对于中部覆盖约束阻尼层的薄壁圆柱壳，求得的固有频率和模态损耗因子如表1所示，三维模态振型图如表2所示，并通过有限元程序ANSYS的结果进行比较，其中单元类型取三维高阶实体单元SOLID186，采用VROATA命令从截面绕轴旋转生成模型，从相邻面扫掠体的方法生成网格，包括2 400个单元和14 580个节点。

由表1可以看出，随着阶次的增加，利用传递矩阵法和有限元法得到的前25阶模态振型变化关系一致，以周向模态振型变化为主，轴向模态振型出现在m=1、2和3，周向振型最高阶出现在n=14，其中，前4阶三维模态振型依次出现在m=1和n=5、6、4、7；第1阶模态振型发生在轴向半波数为1和周向波数为5，对应的固有频率分别为350.36 Hz和347.8 Hz，模态损耗因子分别为0.013 44和0.016 5，通过误差比较可知，固有频率的最大误差值小于2%，模态损耗因子的最大误差值小于7%，说明了采用传递矩阵法对固有频率和模态损耗因子求解的有效性。

表1 局部覆盖粘弹性层合薄壁圆柱壳的固有频率和模态损耗因子Tab.1 Natural frequencies and modal loss factors of a partially covered viscoelastic laminated cylindrical shell

由表1可知，前4阶模态发生在轴向半波数为m=1和周向波数为n=4、5、6、7，则由两种方法求解m=1、2和n=4、5、6、7得到的三维模态振型如表2所示，整体结构的振动位移变化关系一致，反映了构件在悬臂端的振动状态，即在悬臂端处节点的振动位移最大，其中最低阶（1，5）对应的三维模态振型表现为悬臂端周向波数为5的花瓣形状，说明了使用传递矩阵法对三维模态振型求解的有效性。

（2）约束阻尼层位置对振动特性的影响

当基层、阻尼层和约束层的尺寸参数和材料参数不变时，仅改变阻尼层的轴向覆盖位置，当轴向半波数为1时振动特性如图3～5所示。由图3和图4可知，随着周向波数的增加，当约束阻尼层位于薄壁圆柱壳下部时固有频率值最高，固有频率值减小的顺序依次为约束阻尼层位于中部和上部，全覆盖阻尼层时的固有频率值最低，同时上部覆盖阻尼层和全覆盖阻尼层的固有频率值比较接近，固有频率最低的一阶均出现在第（1，5）阶；对于模态损耗因子，当阻尼层位于薄壁圆柱壳下部时模态损耗因子最小，模态损耗因子增加的顺序依次为约束阻尼层位于中部和上部，全覆盖约束阻尼层时的模态损耗因子最高，损耗因子越高时减振效果越好。这是由于约束阻尼层的影响，对基层薄壁圆柱壳起到了约束和耗能作用，当约束阻尼层在下侧时对于整体结构刚度和阻尼影响不大，在上侧时导致了固有频率降低和损耗因子升高，也就更接近于全覆盖约束阻尼层时的情况。

表2 局部覆盖粘弹性层合薄壁圆柱壳的模态振型Tab.2 Three-dimensional modal shapes of a partially covered viscoelastic laminated cylindrical shell

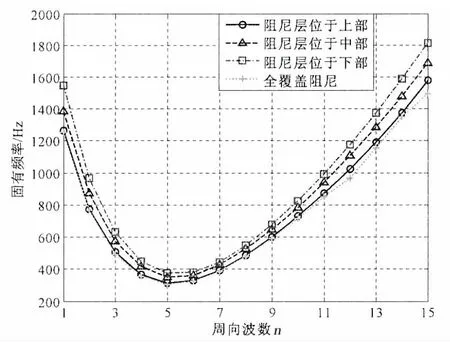
图3 约束阻尼层位置对固有频率的影响Fig.3 The influence of constrained damping layer’s position to natural frequencies

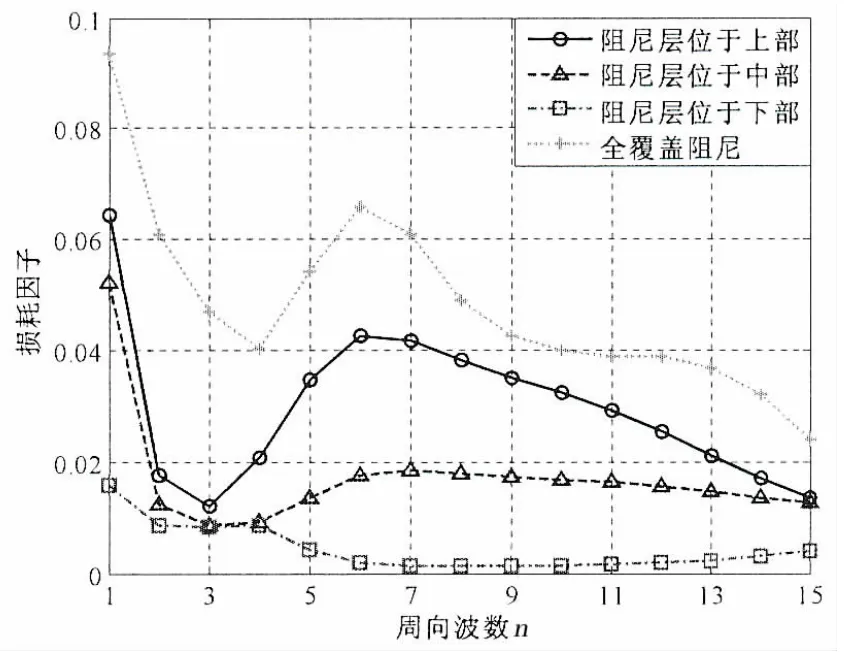
图4 约束阻尼层位置对模态损耗因子的影响Fig.4 The influence of constrained damping layer’s position to modal loss factors

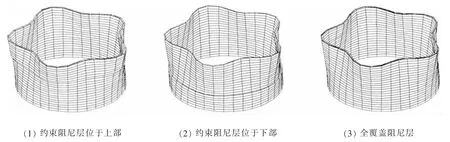
图5 约束阻尼层位置不同时整体结构的三维模态振型Fig.5 Three-dimensional modal shapes with different position of constrained damping layer

当约束阻尼层分别位于薄壁圆柱壳的上部、中部、下部和全覆盖时，以最低阶固有频率对应的振型（1，5）为例，如图5和表2所示，三维模态振型均表现为悬臂端周向波数为5的花瓣形状，这是由于下端是固定的，对于结构有较强的约束，而对于上部约束的影响较小，引起悬臂端的振动位移最大，这一阶也是整体结构最容易发生共振的一阶。

3 结 论

在悬臂边界条件下，通过算例求解得到了环状局部覆盖粘弹层合薄壁圆柱壳的模态振动特性，并通过有限元法进行了比较，主要结论如下：

（1）对于中部覆盖约束阻尼层的薄壁圆柱壳，随着阶次的增加，采用两种方法得到的固有频率的误差值小于2%，模态损耗因子的误差值小于7%，三维模态振型的变化关系一致，并且以周向模态的振动为主，前4阶三维模态振型依次出现在m=1和n=5、6、4、7，固有频率最低的（1，5）阶三维振型表现为周向波数为5的花瓣形状，在悬臂端的振动位移最大，说明了采用传递矩阵法对于此类结构模态振动特性分析的有效性。

（2）当约束阻尼层的覆盖位置不同时，当位于下部时固有频率值最高，固有频率依次减小的顺序为约束阻尼层位于中部和上部，全覆盖时固有频率最低，固有频率最低阶模态振型均出现在（1，5）阶；对于模态损耗因子，当约束阻尼层位于下部时损耗因子最小，数值结果依次增加的顺序为约束阻尼层位于中部和上部，全覆盖时模态损耗因子最高。因此，从结构优化设计和减振效果的角度出发，当约束阻尼层位于上部时的减振效果比较好，应根据实际情况对构件进行减振处理。

[1]黄志诚,秦朝烨,褚福磊.附加粘弹阻尼层的薄壁构件振动问题研究综述[J].振动与冲击,2014,33(07):105-113.Huang Zhicheng,Qin Zhaoye,Chu Fulei.A review about vibration problems of thin-walled structures with viscoelastic damping layer[J].Journal of Vibration and Shock,2014,33(07):105-113.

[2]俞孟萨,刘延利,廖彬彬.腔室内部声场与结构振动耦合特性及噪声控制研究综述[J].船舶力学,2012,16(1-2):191-201.Yu Mengsa,Liu Yanli,Liao Binbin.Summarization on the research of coupling character between cavity acoustics and structure vibration together with noise control[J].Journal of Ship Mechanics,2012,16(1-2):191-201.

[3]王 宇,罗 忠.薄壁圆柱壳构件受迫振动的响应特征研究[J].振动与冲击,2015,34(07):103-108.Wang Yu,Luo Zhong.Study on response characteristics for forced vibrations of thin cylindrical shell[J].Journal of Vibration and Shock,2015,34(07):103-108.

[4]王 宇,翟敬宇,李 晖,等.模态数量对薄壁短圆柱壳振动响应分析的影响[J].噪声与振动控制,2014,34(02):50-55.Wang Yu,Zhai Jingyu,Li Hui,et al.Influence of modal numbers of short thin cylindrical shell on its forced vibration response[J].Noise and Vibration Control,2014,34(02):50-55.

[5]韩清凯,王 宇,李学军.旋转薄壁圆柱壳的高节径振动特性以及篦齿结构的影响[J].中国科学:物理学 力学 天文学,2013,43(04):436-458.Han Qingkai,Wang Yu,Li Xuejun.High nodal diameter vibration characteristics of rotating shell and the effects of its sealing teeth[J].Scientia Sinica Physica,Mechanica＆Astronomica,2013,43(04):436-458.

[6]解妙霞,陈花玲,吴九汇.圆柱壳高频弯曲振动的能量有限元分析[J].西安交通大学学报,2008,42(09):1113-1116.Xie Miaoxia,Chen Hualing,Wu Jiuhui.Energy finite element analysis to high-frequency bending vibration in cylindrical shell[J].Journal of Xi’an Jiaotong University,2008,42(09):1113-1116.

[7]漆万鹏,侯 磊.正交各向异性圆柱壳的轴对称和梁式振动分析[J].船舶力学,2010,14(8):908-914.Qi Wanpeng,Hou Lei.Axisymmetric and beamlike vibration of orthotropic circular cylindrical shell[J].Journal of Ship Mechanics,2010,14(8):908-914.

[8]李 晖,孙 伟,许 卓,等.基于激光旋转扫描的约束态薄壁圆柱壳模态振型测试新方法[J].振动与冲击,2014,33(16):155-159.Li Hui,Sun Wei,Xu Zhuo,et al.Experimental method of laser rotating sanning to measure mode shapes of constrained thin cylindrical shell[J].Journal of Vibration and Shock,2014,33(16):155-159.

[9]Wang H J,Chen L W.Finite element dynamic analysis of orthotropic cylindrical shells with a constrained damping layer[J].Finite Elements in Analysis and Design,2004,40(7):737-755.

[10]Chen L H,Huang S C.Vibrations of a cylindrical shell with partially constrained layer damping(CLD)treatment[J].International Journal of Mechanical Sciences,1999,41(12):1485-1498.

[11]Chen L H,Huang S C.Vibration attenuation of a cylindrical shell with constrained layer damping strip treatment[J].Computers and Structures,2001,79(14):1355-1362.

[12]Sainsbury M G,Mastib R S.Vibration damping of cylindrical shells using strain-energy-based distribution of an add-on viscoelastic treatment[J].Finite Elements in Analysis and Design,2007,43:175-192.

[13]Mastib R S,Sainsbury M G.Vibration damping of cylindrical shells partially coated with a constrained viscoelastic treatment having a standoff layer[J].Thin-Walled Structures,2005,43:1355-1379.

[14]Mohammadi F,Sedaghati R.Linear and nonlinear vibration analysis of sandwich cylindrical shell with constrained viscoelastic core layer[J].International Journal of Mechanical Sciences,2012,54:156-171.

[15]李恩奇,李道奎,唐国金,等.基于传递函数方法的局部覆盖环状CLD圆柱壳动力学分析[J].航空学报,2007,28(6):1487-1493.Li Enqi,Li Daokui,Tang Guojin,et al.Dynamic analysis of cylindrical shell with partially covered ring-shape constrained layer damping by the transfer function method[J].Acta Aeronautica et Astronautica Sinica,2007,28(6):1487-1493

[16]杨少红,王安稳.基于混合分层理论的粘弹层合圆柱壳的阻尼振动和层间应力研究[J].工程力学,2008,25(3):38-42.Yang Shaohong,Wang Anwen.Damping vibration and interlaminar stresses atudy using mixed layerwise theories for viscoelastic laminated cylindrical shell[J].Engineering Mechanics,2008,25(3):38-42.

[17]王祖华,彭 旭,谢官模.部分敷设阻尼层的有限长环肋圆柱壳声辐射计算方法研究[J].船舶力学,2010,14(4):430-438.Wang Zuhua,Peng Xu,Xie Guanmo.Sound radiation from submerged finite ringstiffened cy-lindrical shells,partially covered with compliant layers[J].Journal of Ship Mechanics,2010,14(4):430-438.

[18]曹雄涛,张志谊,华宏星.约束层阻尼圆柱壳的自由振动[J].应用数学和力学,2011,32(4):470-482.Cao Xiongtao,Zhang Zhiyi,Hua Hongxing.Free vibration of circular cylindrical shell with constrained layer damping[J].Applied Mathematics and Mechanics,2011,32(4):470-482.

[19]李 超,李以农,施 磊,等.圆柱壳体阻尼材料布局拓扑优化研究[J].振动与冲击,2012,31(4):48-52.Li Chao,Li Yinong,Shi Lei,et al.Topological optimization for placement of damping material on cylindrical shells[J].Journal of Vibration and Shock,2012,31(4):48-52.

[20]王 淼,孟 光,方之楚,等.夹层圆柱壳振动的谱有限元分析[J],应用力学学报,2009,26(4):715-720.Wang Miao,Meng Guang,Fang Zhichu,et al.Spectral finite element analysis for vibration of sandwiched shell[J].Chinese Journal of Applied Mechanics,2009,26(4):715-720.

[21]Soedel W.Vibrations of shells and plates[M].CRC Press,2004.

[22]向 宇,黄玉盈,黄健强.一种新型齐次扩容精细积分法[J].华中科技大学学报(自然科学版),2002,3(11):74-76.Xiang Yu,Huang Yuying,Huang Jianqiang.A method of homogenization of high precision direct integration[J].Journal Huazhong University of Science and Technology(Nature Science Edition),2002,30(11):74-76.

Study on vibration characteristics of a ring covered viscoelastic laminated cantilever thin cylindrical shell

WANG Yu1,ZHAI Jing-yu2,LI Chang1,SONG Hua1
(1.School of Mechanical Engineering,University of Science and Technology Liaoning,Anshan 114051,China;2.School of Mechanical Engineering,Dalian University of Technology,Dalian 116024,China)

Vibration characteristics of a ring covered viscoelastic laminated cantilever thin cylindrical shell are studied by transfer matrix method.A first-order ordinary differential equations for the host shell and the constraining layer are established based on Love’s shell theory combining with deformation coordination of viscoelastic damping layer and interactional forces,and an integrated transfer matrix of the whole component is derived by transfer matrix method.Then,the natural frequencies,loss factors and three-dimensional shapes are derived by high-precise integration method,and its vibration characteristics are discussed when the covered position is different.Finally,the results are compared with results of finite element method.The example results show that transfer matrix method is effective to solve the vibration characteristics of the ring covered viscoelastic laminated cantilever thin cylindrical shell,and the main modal vibration occurs in the circumferential direction.The three-dimensional modal shape corresponding to the lowest order natural frequency is(1,5),and the cantilever’s vibration displacement is maximum.At the same time,the covered location of constrained damping layer has obvious impact on modal characteristics of the thin cylindricalshell.

viscoelastic laminated thin cylindrical shell;cantilever boundary condition;ring covered;three-dimensional modal shape

O326 TH113.1

A

10.3969/j.issn.1007-7294.2017.11.009

1007-7294（2017）11-1393-11

2017-05-18

辽宁省科技厅博士科研启动基金项目（201601295）；辽宁省教育厅自由探索重点项目（2016TSZD07）；辽宁科技大学优秀人才项目

王 宇（1979-），男，博士，讲师，E-mail：wangyu435@126.com；

翟敬宇（1983-），男，博士，讲师。