囊式空气弹簧机械阻抗特性研究

李鹏辉 ， 帅长庚 ， 王锁泉 ， 彭桂初

（1.海军工程大学 a.振动与噪声研究所；b.船舶振动噪声重点实验室，武汉 430033；2.中国船舶科学研究中心，江苏无锡214082；3.中国人民解放军九二二六七部队，山东青岛266000）

囊式空气弹簧机械阻抗特性研究

李鹏辉1a，b， 帅长庚1a，b， 王锁泉2， 彭桂初3

（1.海军工程大学 a.振动与噪声研究所；b.船舶振动噪声重点实验室，武汉 430033；2.中国船舶科学研究中心，江苏无锡214082；3.中国人民解放军九二二六七部队，山东青岛266000）

根据小幅振动的线性叠加原理将囊式空气弹簧分成几个简单的可解析计算的规则区域，结合线性空气波动理论求解出空气弹簧内部声压场的分布。根据弹性薄壳无矩理论推导出旋转壳体状态向量的一阶常微分矩阵方程，利用齐次扩容精细积分法推导出壳体的传递矩阵，结合动力平衡方程求出空气弹簧在位移谐波激励下所受到的激励力，进而得出其机械阻抗。算例结果表明该方法合理可行，为运用近似解析法分析空气弹簧的阻抗特性提供了一种新的思路。

旋转薄壳；线性空气波动理论；传递矩阵法；齐次扩容精细积分法；机械阻抗

0 引 言

空气弹簧是以密封空气为介质对设备进行支撑与隔振的一类隔振元件，囊式空气弹簧以其固有频率低、刚度可调、不存在“蠕变”等优点在船舶动力装置中得到了广泛的应用。机械阻抗是弹性元件隔振设计和性能优化的主要指标[1]，机械阻抗的获取主要有实验测试和解析计算两种途径，由于材料非线性、几何结构复杂等原因使得机械阻抗的获取一般都依赖于实验[2]。采用解析法可以定性定量地分析阻抗特性，为空气弹簧的设计、使用提供理论依据，因此能够正确有效地采用解析法分析机械阻抗具有重要的意义。孙健等人[3]通过分析圆柱型橡胶隔振器的阻抗特性指出了传统地将隔振器简化为弹簧和阻尼模型的不足，并且指出了高频波动的问题；顾太平等人[4]结合帘线平衡角用近似解析算法分析了空气波动对机械阻抗的影响规律，指出了空气弹簧内部声压场与壳体应力场之间的耦合问题。

传递矩阵法是由Tottenham与Irie等人[5-6]提出并不断发展的分析壳体振动的一种半解析半数值的方法，它的优点是壳体中每个壳体微元的状态向量都可以用相应的传递矩阵来表示，进而可以得到壳体两端支撑处状态向量之间的关系，因此传递矩阵法在分析壳体振动方面得到了广泛的应用[7-8]。传统的传递矩阵分析方法有一个局限性是壳体的状态方程必须是一阶齐次常微分的矩阵形式，这限制了该方法的应用。对于该问题，苏海东、黄玉盈等人[9-10]提出了扩容精细积分法，该方法通过将非齐次的状态方程扩容成齐次的状态方程，拓展了传递矩阵法的使用范围。

本文将囊式空气弹簧划分为几个规则的区域，求解出各个区域内部的声压方程，通过衔接处理得到各个区域之间声压的关系。将壳体划分为有限个细小的微元壳体，采用齐次扩容技术得出每个壳体微元两端面间的齐次扩容状态矩阵方程，再由精细积分法得出整个壳体两端的矩阵方程，结合动力平衡方程可以得出空气弹簧的机械阻抗表达式。

1 数学模型

简化的回转型囊式空气弹簧模型是由上下盖板、囊体以及内部空气组成，将内部空气的区域分解为矩形回转体与弧形回转体，机械阻抗计算模型如图1所示，下盖板固定，上盖板受到位移简谐激励，以上盖板面中心为原点建立柱坐标系orz。

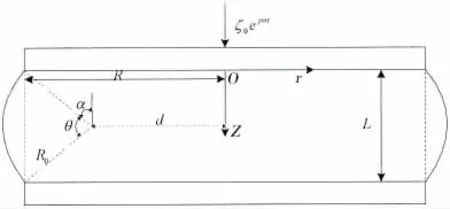
图1 囊式空气弹簧机械阻抗计算模型Fig.1 The mechanical impedance calculation model of bellows type air spring

1.1 声压方程的推导

当上盖板受到激励时，空气弹簧内部声压发生复杂的变化，为了便于计算，将内部空气区域划分为矩形回转体与弧形回转体，将矩形回转体内的运动分为垂向运动与横向运动。求解声压方程转变为亥姆霍兹方程在边界条件下的定值求解问题。

对于矩形回转体内空气体积元的垂向运动，边界条件是：

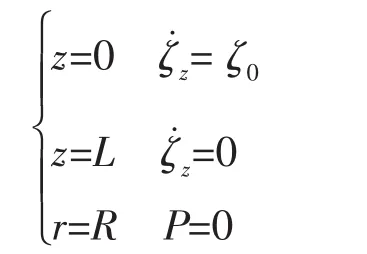
求解出空气体积元垂向运动所产生的声压以及径向速度表达式分别为：

对于矩形回转体内空气体积元的横向运动，假设在矩形回转体与弧形回转体交界处空气流速为，空气单元横向运动的边界条件为：

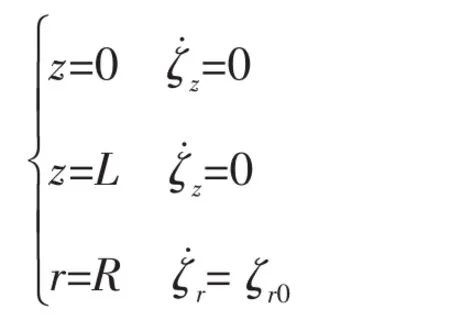
求解出空气体积元横向运动所产生的声压以及径向速度表达式分别为：

由于弧形回转体形状不规则，为了便于求解，近似地认为其内部声压值相等，将其等效为亥姆霍兹共鸣器来进行处理。两个回转体交界处的面积与弧形回转体的体积分别为：

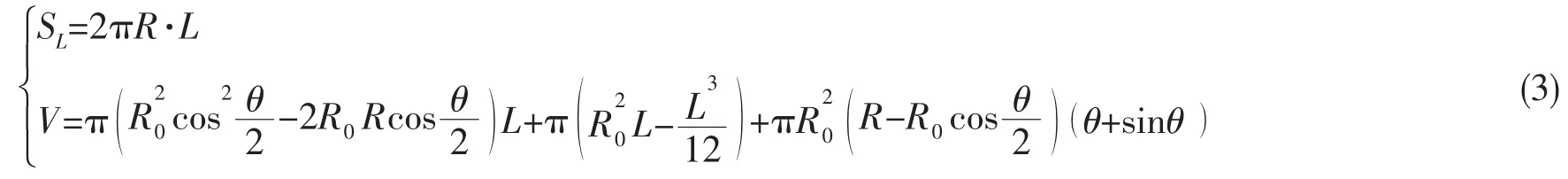
弧形回转体与矩形回转体交界处的边界条件是声压值与空气流量相等，即在r=R处有：

1.2 壳体传递矩阵的推导

建立正交曲线坐标系，以径向参数α与纬向参数β作为变量，截取囊体曲边dα、dβ微元，微元受力分析如图2所示。图中N1、N2分别表示经线与纬线方向单位长度所受到的拉压力，R1、R2表示主曲率半径，p表示囊体在法向方向上所受到的压力，假设空气弹簧初始压力为p0，则p=p0+p3。由几何知识可得沿 α、β方向的拉密系数分别为：A=R0，B=R0sinα+d。

设囊体的弹性模量为E，泊松比为μ，密度为ρ，厚度为δ，用U、W分别表示沿α、β方向上的位移。根据弹性薄壳无矩理论可以得到囊体振动的动平衡方程和弹性方程。动平衡方程为：

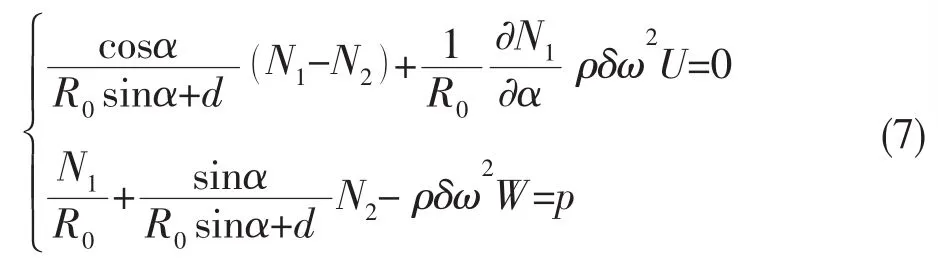
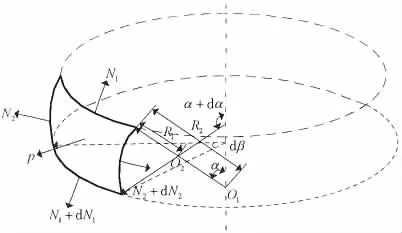
图2 囊体微元受力分析Fig.2 Mechanical analysis of the micro element for bellows

弹性方程为：

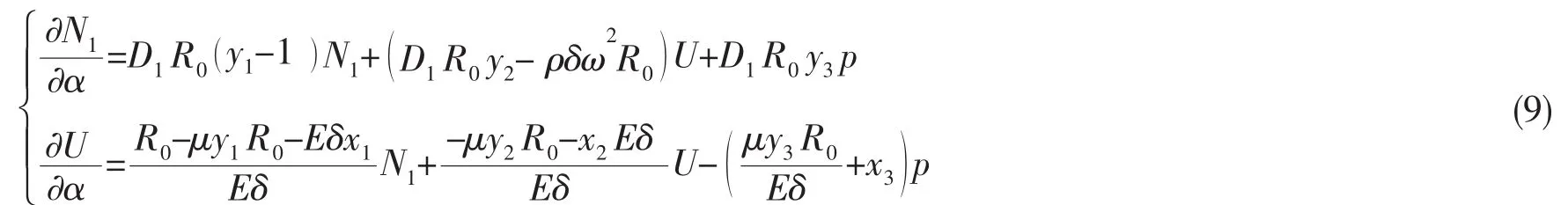
将（9）式写成矩阵的形式：

该表达式是一个非齐次的变系数矩阵微分方程，本文借鉴文献[10]提出的思路，先对这个方程进行齐次化和常数化，然后再用精细积分法进行求解。

囊体的弧度θ=2π/3，在沿α方向剖分积分弧段时将其分成n等份，则每一等份的弧度是Δα=θ/n。对于（10）式中的非齐次项结合泰勒公式展开，用二次式逼近可得：

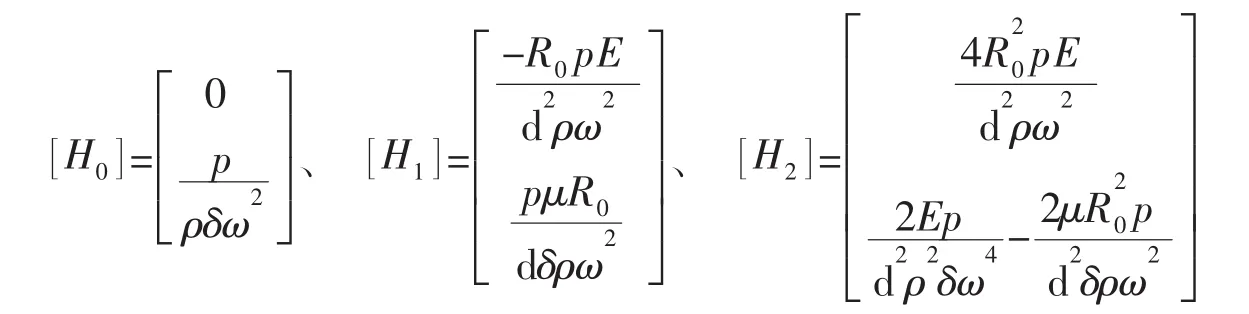
上式各项中都含有表达式D1、D2，它们是关于变量α的函数，当积分弧段足够小时可用D1、D2的平均值来代表它在该段的值。以第i段积分弧段为例可得：

此时的齐次扩容矩阵微分方程为：

由（14）式可得传递矩阵表达式为：

由精细积分法[11]可得：

囊体两个端面之间的传递矩阵为：

可得囊体两端支撑处状态向量之间的关系式为：

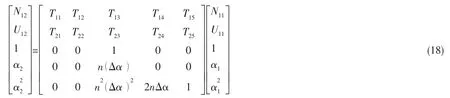
沿α方向上的应力和位移之间的关系是：

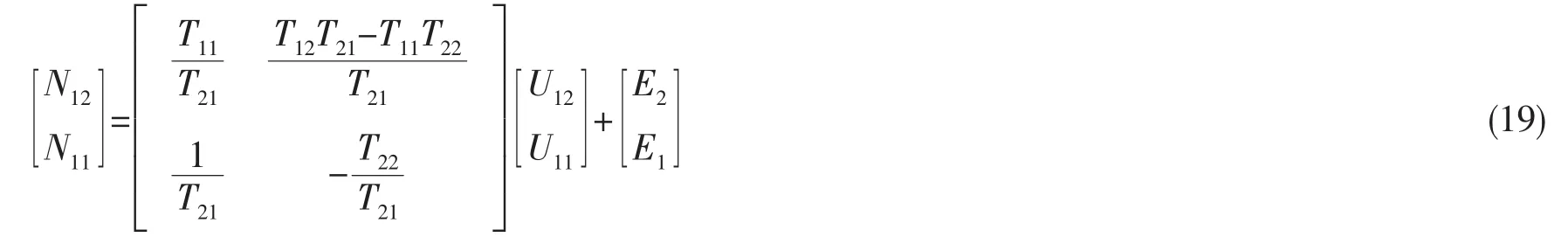
1.3 机械阻抗表达式的推导

上盖板受到位移简谐激励时，空气弹簧内部声压场对上下盖板处的动态力为：

对囊体上下端面由几何关系可知：

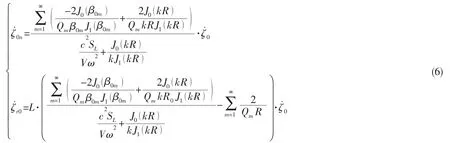
当空气弹簧下盖板固定时囊体下端U1=0，可得囊体所受到的动态力表达式为：

对上下盖板结合动力平衡方程以及机械阻抗的定义可得输入阻抗Z11与传递阻抗Z12表达式分别为：

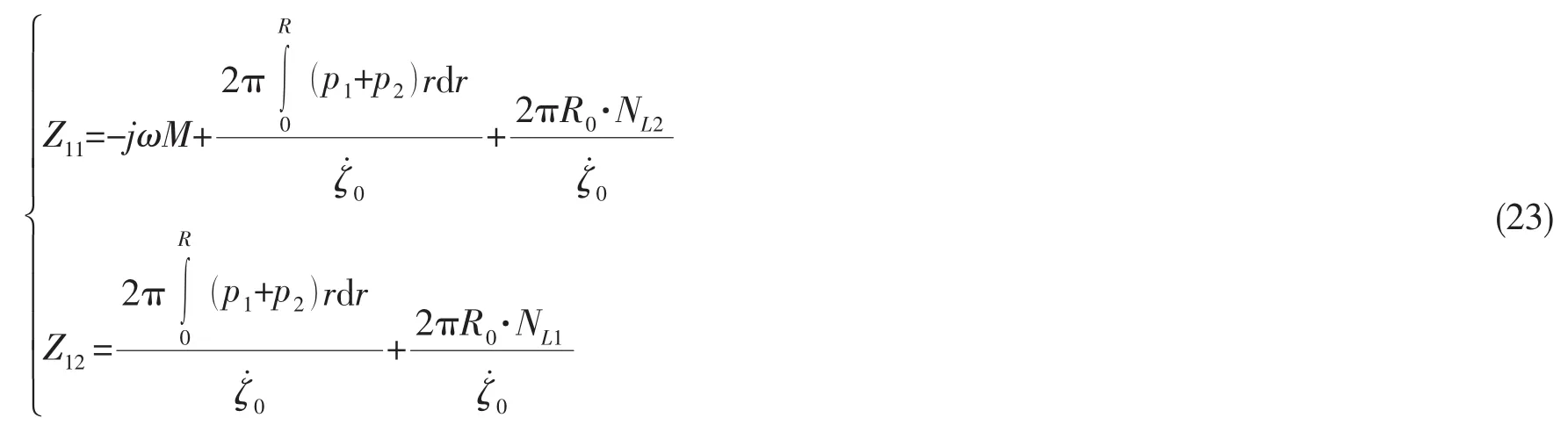
式中：M表示上盖板的质量，α1、α2分别表示壳体在上下端面处经线方向上的坐标。

2 仿真验证与分析

假设初始压力为3[atm]，表1给出了囊式空气弹簧阻抗计算所需的各项参数。

表1 空气弹簧阻抗计算参数Tab.1 Parameters used in impedance calculation of air spring

图3 不同激励频率时的声压场分布Fig.3 The acoustic pressure distribution at different excitation frequency

采用Comsol Multiphysics软件中的声固耦合模块，对下盖板施加固定约束，上盖板施加位移简谐激励来模拟空气弹簧的简谐振动。计算结束后，与（23）式结合可得气囊机械阻抗计算与仿真结果的对比如图4所示，由图可知计算结果与仿真结果吻合良好，验证了本文提出的通过传递矩阵来分析气囊机械阻抗特性方法的可行性。

图4表明：气囊机械阻抗曲线表现出了明显的刚度区、共振区与质量区，当激励频率比较高时出现明显的波动效应。各区域的划分是由刚度与盖板质量这两个因素共同作用的；刚度区是在低频段，此时气囊刚度起主导作用，随着频率的增加刚度与质量的作用平分秋色，此频段为共振区，随着激励频率的进一步提高，在高频段质量起到主导作用，表现为质量区。

3 结 语

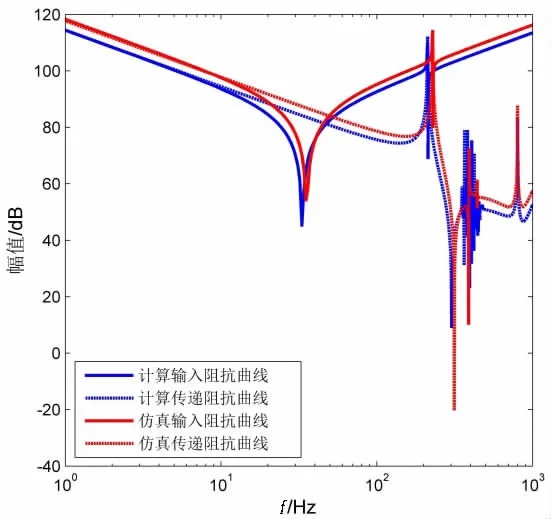
图4 机械阻抗计算与仿真的对比Fig.4 The contrast of mechanical impedance between arithmetic and FEM simulation

本文计算了空气弹簧内部的声压场，借助齐次扩容技术与精细积分法得出壳体两端的状态矩阵方程，与声压场结合用近似解析法求解出了空气弹簧的阻抗特性，经验证该方法合理可行，为用解析法分析空气弹簧的阻抗特性提供了一种新的求解方法，该方法可推广应用到管路系统阻抗特性的分析，这对于空气弹簧以及空气管路系统减振元件的传递特性研究具有重要的借鉴意义。

本文提出的近似解析方法误差来源主要有三个方面：一是（11）式中对非齐次项函数的二次式逼近；二是（10）式中系数矩阵中随坐标α变化的变量D1，D2，在一个足够小的积分弧段内用平均值在代替；三是求解声压场时对弧形回转体的近似处理。对误差来源一、二来讲，本文提出的方法不但考虑了弧形管管壁截面积的变化也考虑到了其结构的变化，比起简单地将其简化为变截面杆模型，该方法精度更高。需要进一步完善的地方是误差来源三，如何能够更加精确地求解出弧形体内的声压分布还有待于进一步地深入研究。

[1]王锁泉,周庆云,席亦农,等.隔振元件机械阻抗测量与数据处理方法研究[J].舰船科学与技术,2006,28(2):107-111.Wang Suoquan,Zhou Qingyun,Xi Yinong,et al.Study on the measurement technique and data processing on mechanical impedance of vibration isolator elements[J].Ship Science and Technology,2006,28(2):107-111.

[2]王汉刚,帅长庚,郭 伟.气囊隔振器垂向阻抗及其传递特性研究[J].噪声与振动控制,2010,21(2):192-195.Wang Hangang,Shuai Changgeng,Guo Wei.Study on the vertical impedance and transfer characteristic of pneumatic vibration isolator[J].Noise and Vibration Control,2010,21(2):192-195.

[3]孙 健,朱石坚,吕志强.隔振器机械阻抗特性研究[J].船海工程,2003,4:25-29.Sun Jian,Zhu Sijian,Lv Zhiqiang.Study on the mechanical impedance of the vibration isolator[J].Shipamp;Ocean Engineering,2003,4:25-29.

[4]顾太平,何 琳,付 钰.囊式空气弹簧机械阻抗近似解析算法研究[J].振动与冲击,2012,30(2):196-198.Gu Taiping,He Lin,Fu Yu.Approximate analytic algorithm for mechanical impedance of bellows typeair spring[J].Journal of Vibration and Shock,2012,30(2):196-198.

[5]Tottenham H,Shimizu K.Analysis of the free vibration of cantilever cylindrical thin elastic shells by the matrix progression method[J].International Journal of Mechanical Sciences,1972,14:293―310.

[6]Irie T,Yamada G,Kaneko Y.Free vibration of a conical shell with variable thickness[J].Journal of Soundamp;Vibration,1982,82(1):83―94.

[7]雷勇军,周建平.圆锥壳自由振动传递函数解[J].上海力学,1998,19(3):235-243.Lei Yongjun,Zhou Jianping.Transfer function solution on free vibration of conical shells[J].Shanghai Journal of Mechanics,1998,19(3):235-242.

[8]李 琳.旋转薄壳自由振动的精确解法[J].航空动力学报,1997,12(2):117-121.Li Lin.An exact solution for free vibration of toroidal thin shell[J].Journal of Aerospace Power,1997,12(2):117-121.

[9]Xiang Yu,Huang Yuying.A semi-analytical and semi-numerical method for solving 2-D sound-structure interaction problems[J].Acta Mechanical Solida Sinica,2003,16(2):116-126.

[10]苏海东,黄玉盈.分析旋转薄壳的传递矩阵法[J].工程力学,2008,25(9):1-6.Su Haidong,Huang Yuying.A transfer-matrix method for analyzing revolutionary shells[J].Engineering Mechanics,2008,25(9):1-6

[11]钟万勰.结构动力方程的精细时程积分法[J].大连理工大学学报,1994,34(2):131-136.Zhong Wanxie.On precise time-integration method for structural dynamics[J].Journal of Dalian University of Technology,1994,34(2):131-136.

Study on the mechanical impedance of bellows type air spring

LI Peng-hui1a,b,SHUAI Chang-geng1a,b,WANG Suo-quan2,PENG Gui-chu3
(1a.Institute of Noiseamp;Vibration;1b.National Key Laboratory on Ship Vibrationamp;Noise,Naval University of Engineering,Wuhan 430033,China;2.China Ship Scientific Research Center,Wuxi 214082,China;3.92267 Troop of People’s Liberation Army,Qingdao 266000,China)

The bellows type air spring was divided into several calculable regular simple regions according to superposition principle,and the sound pressure distribution was calculated based on the linear air wave theory.Based on the non-moment theory of elastic thin shell,the 1-order ordinary differential matrix equation for the state vector of revolutionary shells was derived.The transfer-matrix of the shell was derived by extended homogeneous capacity high precision integration method and the exciting force of the air spring under displacement harmonic excitation was achieved by combined with dynamical balancing equation,then the mechanical impedance of the air spring was derived.The results show that the proposed method is feasible and it provides a new idea to analyse the mechanical impedance characteristics of the air spring with the method of approximate analytic algorithm.

revolutionary thin shell;linear air wave theory;transfer-matrix method;extended homogeneous capacity high precision integration method;mechanical impedance

O328

A

10.3969/j.issn.1007-7294.2017.11.014

1007-7294（2017）11-1440-08

2017-08-05

教育部“新世纪优秀人才支持计划”资助

李鹏辉（1992-），男，硕士研究生，E-mail：lph0115@163.com；

帅长庚（1975-），男，教授，博士生导师，通讯作者，E-mail：chgshuai@163.com。