近地、水面时的飞行器动态稳定特性数值模拟

米百刚，詹 浩

（西北工业大学 航空学院，西安 710072）

近地、水面时的飞行器动态稳定特性数值模拟

米百刚，詹 浩

（西北工业大学 航空学院，西安 710072）

基于非结构动态网格重构技术，采用SA模型以及VOF方法，分别对NACA0012二维翼型自由空间、近地效应以及近水面效应的非定常运动流场进行了数值计算分析，并根据建立的基于小幅度强迫振动的组合动导数辨识方法计算了各个攻角下动导数。计算结果分析表明动导数计算方法准确可靠；中小攻角下，地面与水面以管道效应影响流场，均损失了动态阻尼，柔性的水面损失更多，动导数绝对值更小；大攻角时，两者表现为阻塞效应，柔性水面下的动态阻尼增大，动导数绝对值也变大；相比地面效应，柔性的水面影响范围更广。

自由空间；地面效应；水面效应；动导数；数值模拟；计算流体力学

0 引 言

当飞行器贴近地面或者水面飞行时，受到地面或者水面效应的影响[1-2]，飞行器的气动力会发生不同于无限空间自由流场的变化，充分地利用这些效应可以设计出地效飞行器，此类飞行器载重量大，经济性好，无需专门修建的起降场地，低空飞行隐蔽性好，无论是在民用还是军用上都有着非常广阔的前景，因而得到了世界各国的重视。同时，随着飞行器气动设计的快速发展，非定常动态特性的研究成为一个热点，与其相关的现象如飞行器的颤振，动态操纵以及动态稳定性等在当前的飞行器设计中表现得越来越重要，无论是针对常规飞行器还是地效飞行器。

目前对于地效飞行器的气动特性的研究多集中在常规的气动力分析计算上。比如国内的盛其虎[3]使用面元法来对风浪扰动中的飞行器非定常气动力进行了计算分析；邹光远等[4]发展了边界元法来求解近水面飞行时的全机气动力水波效应，给出了水波效应随攻角、飞行高度、入射角等参数的变化；刘沛清等[5-6]使用基于求解NS方程的方法对飞行器的波浪地面以及波浪水面上的气动力进行了数值计算，分析了飞行器在不同波长、波高等因素影响下的气动力变化特性，较为精确地揭示了地面以及水面对飞行器的气动设计的影响作用。国外的研究中，Schweikhard[7]采用离散涡模型计算了二维机翼的动态地面效应，NAhait[8]则采用涡格法建立了计算三维地效机翼的数值方法并考虑了厚度的影响；Kornev等[9]基于涡格法以及非定常线化理论假设发展了估算地效下的复杂构型气动导数的数值方法。可以看出，目前的研究对飞行器地、水面效应下的非定常动态运动特性涉及很少，而地效飞行器长时间贴近地面或者水面飞行，其动态运动时引起的非定常气动力特性与常规飞行器有很大差别，因而，分析研究地效飞行器动态运动气动特性十分迫切。

本文结合非定常动态非结构网格重构技术，基于求解非定常NS方程，对二维翼型贴近地面以及水面飞行时的非定常动态运动流场进行数值模拟研究，对表征非定常动态稳定性的指标—动导数进行计算，分析不同近地/近水高度对动导数的影响。结果表明，地面/水面的存在剧烈地影响了翼型的动态稳定特性，近地/近水高度不同，影响程度也不一样，同样高度下，地面与水面的影响程度也存在差异，说明在地效飞行器的非定常空气动力设计中，地面、水面的干扰应该被综合统筹考虑。

1 控制方程

文中采用二维积分形式的非定常雷诺平均N-S方程，即

其中：V0为任意控制域；W是守恒变量；F为无粘 （对流）通矢量项；Fv为粘性通量；∂V0为控制域的边界；n为控制域边界单位外法向矢量；Re为计算的雷诺数。

空间离散采用二阶迎风格式—量差分分裂（Roe-FDS）格式，使用用LU-SGS双时间时间推进法求解非定常控制方程。湍流模型使用SA一方程模型。

2 VOF模型

本文的计算涉及到水面上的非定常气动力计算，此时的介质包括水和空气，因此使用VOF模型定义自由水面。VOF模型是一种在固定的欧拉网格下的表面跟踪方法，通过求解单独的动量方程和处理穿过区域的每一流体的体积分数来模拟两种或三种不能混合的流体。当需要得到一种或多种互不相融流体间的交界面时，可以采用这种模型。典型的应用包括分层流、射流破碎、流体中的大泡运动、自由表面流动等。

采用VOF方法模拟自由水面，用几何重构方案模拟气液界面，并对水气交界区域网格进行了加密。VOF模型中定义了一个体积函数αq，代表第q种流体占控制体的体积分数，在每个控制体当中，所有流体的体积分数之和等于1，即αq=1表示流体当中充满第q种流体，αq=0表示流体中不含有第q种流体，0＜αq＜1表示控制体中含有第q种流体的体积分数为αq。自由界面处满足体积分数方程：和计算控制条件两种流体混合的单元采用如下公式计算密度：

动量方程为

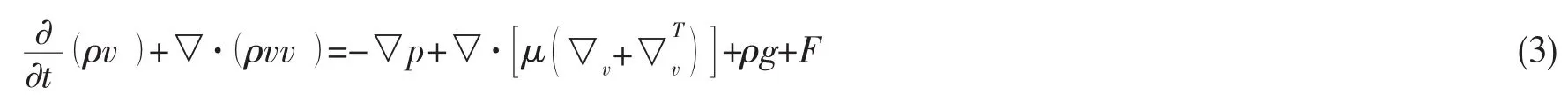
3 动稳定性导数计算方法及其验证

3.1 计算方法

动导数[10-12]是表征飞行器动态稳定特性的指标，它是飞行器六个气动系数（即三维直角坐标系中的三个力和三个力矩系数）对飞行器姿态参数时间的变化率的导数，是飞行器导航系统，控制系统以及动态品质分析不可缺少的原始气动参数，直接影响着飞行器的飞行品质。

以纵向为例，阐述本文求解动导数的方法。强迫飞行器做小幅度俯仰振荡时，刚体飞行器所受非定常气动力矩可以表示为：

上式实际上是对刚体飞行器小振幅强迫振动所受非定常气动力矩进行了泰勒展开，其中为气动力矩静导数，为气动力矩对迎角的一阶动导数，为气动力矩对俯仰角速度的零阶动导数，为气动力矩对俯仰角速度的一阶动导数，为高阶导数项。

当刚体飞行器以低频ω做小幅度振荡时，其模型运动方程可以简化为：

展开（2）式并略去高次谐波分量，同时将（4）式代入略去高阶分量Δ赞，整理同类项可得：

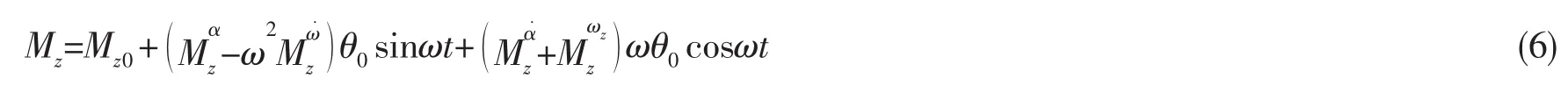
当非定常问题计算足够长时，令ωt=2nπ，就可以抹去初始效应的影响，气动力矩达到一个周期性稳态值，于是（5）式可以写为：

至此，基于傅立叶及泰勒展开方法推导出了纵向组合导数的表达式（7）。

根据国家标准，减缩频率取为k=ωl/2V*，其中l为参考长度，V*为远场自由来流速度，代入可得无量纲化动导数计算公式（8）

基于此方法，通过CFD方法得到稳态气动力以及非定常周期气动力即可数值求解无限空间自由流场、地面效应以及水面效应影响下的动导数。

3.2 标准算例验证

动导数的计算主要在于准确地求解非定常气动力及力矩系数。本节对前面开发的非结构网格的翼型动态特性的数值模拟方法进行验证。验证算例为AGARDCT3[12]，NACA0012翼型的运动状态可以写为

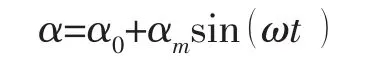
其中：α0=4.86°，αm=2.44°，减缩频率 k=ωc/2V=0.080 8。

计算马赫数为Ma=0.6，基于弦长c的雷诺数为480万，翼型绕1/4弦长处做俯仰运动，力矩系数参考位置也选择此点。图1分别为使用本文方法计算得到的非定常法向力系数及俯仰力矩系数随迎角的变化曲线，可以看出，计算值与试验值符合得很好，本文的非定常强迫振动方法能够很好地预测迎角与力/力矩系数之间的迟滞效应。

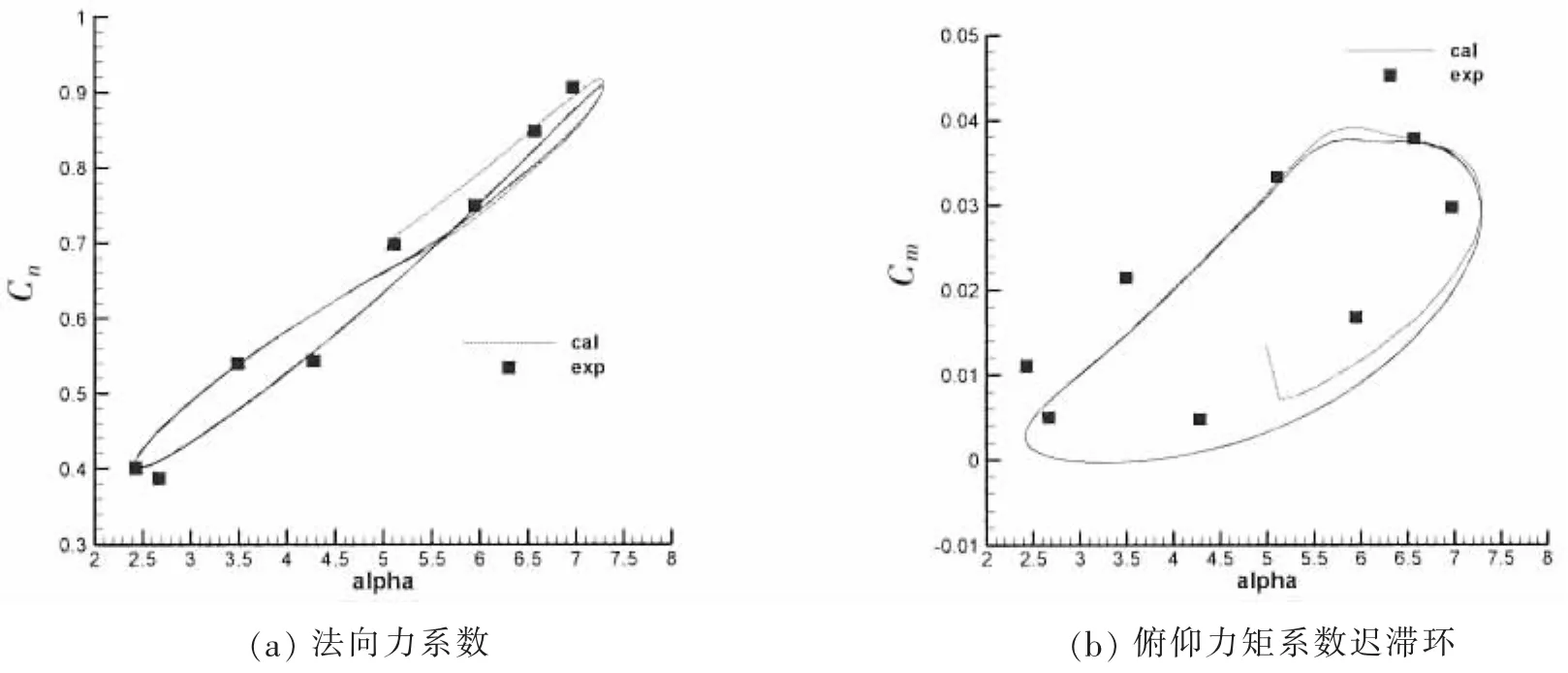
图1 非定常气动力/力矩系数迟滞环Fig.1 Hysteresis loops of unsteady aerodynamic force and moment coefficient

根据本文的动稳定性导数计算方法可以计算得到该状态下的动导数为-3.342 3，与文献值的-3.41吻合得较好。

4 计算模型、网格以及边界条件

本文的计算针对三种情况进行对比：一是无限空间自由流场下的的动导数计算；二是考虑地面效应的动导数计算；三是考虑柔性水面效应的动导数计算。

这三种情况的计算模型、网格及边界条件各不相同，分别论述如下：

第一种情况是常规的飞行器在无限空间自由流场运动的情形，此时的计算模型及网格分别见图2（a）、（b），边界条件包括远场（farfield）以及无滑移壁面边界条件。

第二种情况是考虑地面效应影响的情形，此时翼型下部的边界被地面所代替，所采用的边界条件为滑移壁面条件，用来模拟地面相对飞行器的运动。翼型表面为无滑移壁面条件，其余边界为远场条件。计算模型和网格分别见图3（a）、（b），图中V为自由来流速度，h为翼型尾缘点距离地面（水面）的距离，使用h/c来表示这一高度的相对值。

第三种情况是考虑水面影响的情形，此时翼型下部为具有一定深度的液态水，水面上的空气部分边界条件为速度入口，压力出口，上部以及右部的出口与大气相通；水面下的部分同样是速度入口，压力出口，此时的压力由使用P=ρghw计算得到不同水深处的压力，底部的壁面为滑移壁面。为了更为清晰地捕捉水面，交界附近的网格进行了加密。图4（a）、（b）分别显示了水面影响时的计算模型以及网格。

图2 无限空间自由流场Fig.2 Free flow field

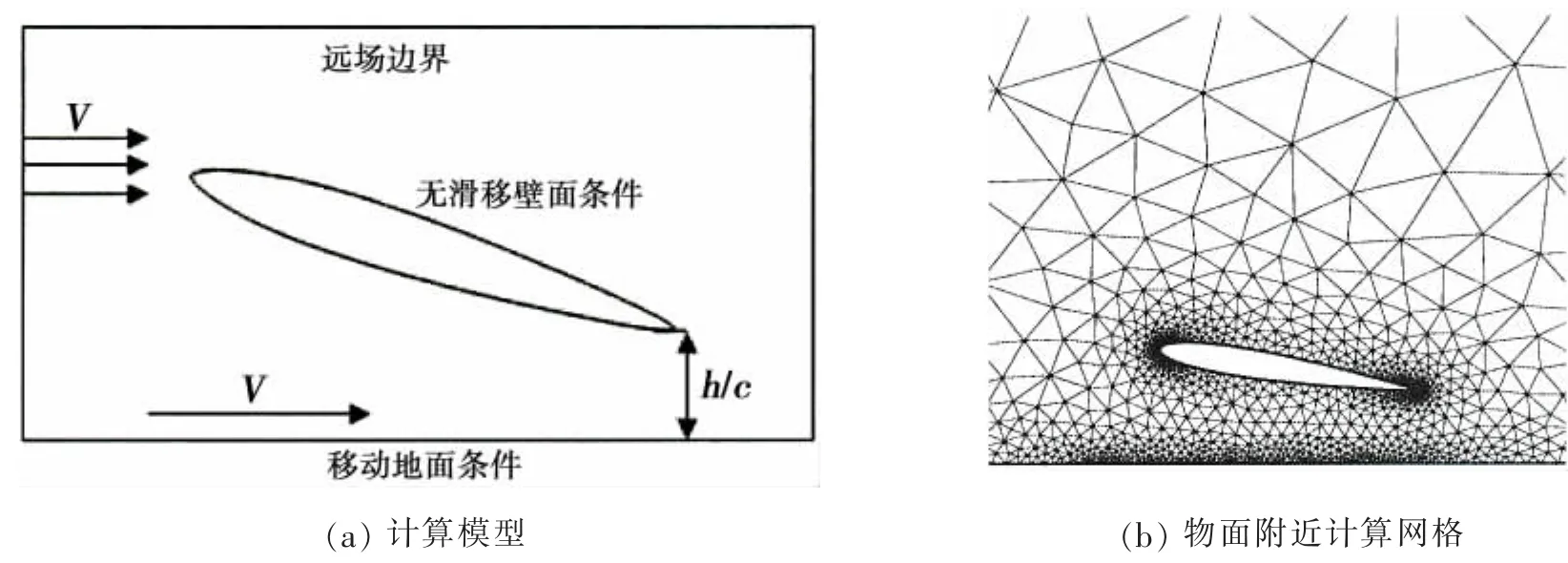
图3 地面效应Fig.3 Ground effect

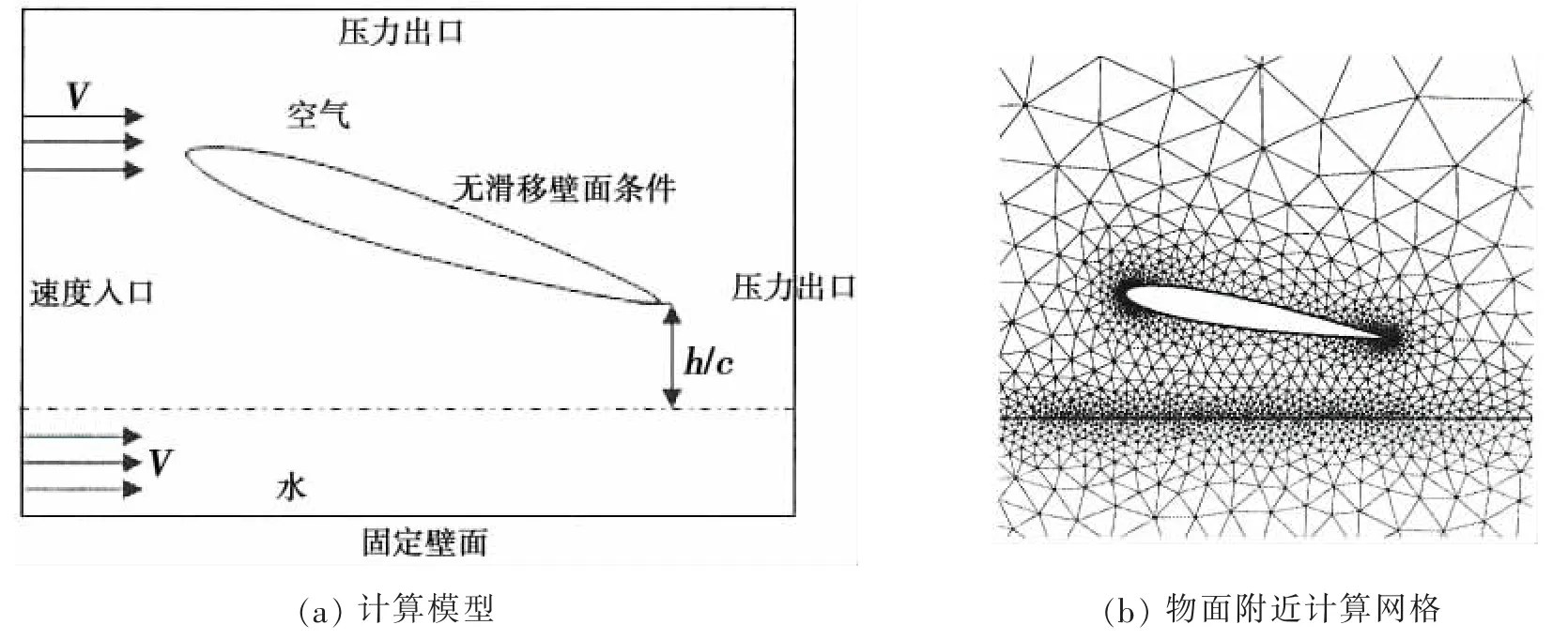
图4 水面效应Fig.4 Water surface effect

5 计算结果及分析

自由空间、地面效应以及水面效应的计算状态如下：

马赫数Ma=0.2

计算攻角：0、2、4、6、8 及 10 度

近地/水高度：h/c=1，2，5

减缩频率为：

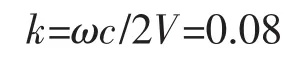
非定常运动的运动形式为：

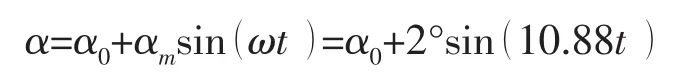
其中：α0为初始攻角。

利用文中建立的基于非结构网格重构的方法实现非定常运动流场的求解，得到的非定常气动力/力矩呈现周期性的变化，并且相比瞬时迎角的变化呈现明显的迟滞效应，这是非定常运动的一个特点，图5（a）、（b）分别显示了0°以及8°攻角时的俯仰力矩系数随瞬时攻角变化的迟滞环曲线，可以看出，由于近水面效应的复杂性，非定常运动曲线的光滑程度不如近地以及无限空间自由流场状态，同时，当h/c=5时，各个攻角下的近地效应俯仰力矩系数迟滞环曲线与无限空间的结果基本一致，但是水面影响的曲线依然相差很大，这更加清晰地说明了水面的存在影响范围更广。

图6-9为初始攻角为10°时翼型上仰到瞬时攻角为10.79°的三种计算模型的物面压力系数以及流场图。由于有了地面和水面的影响，翼型的上下翼面的压力系数均发生了变化，而相比之下，地面和水面影响下的上翼面压力系数基本一致，但是显然近水面时的下翼面的压力系数更高，从而导致整体的瞬时升力较近地面效应大。

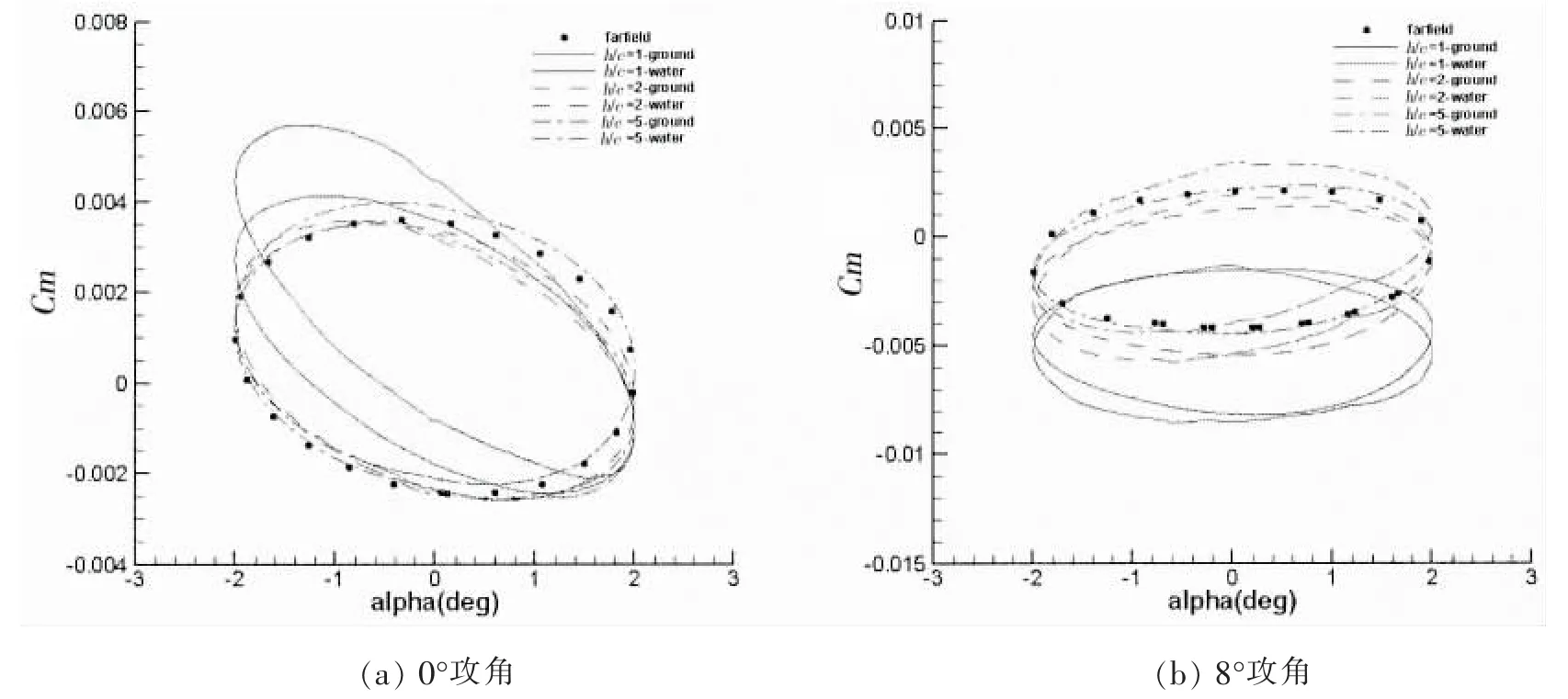
图5 俯仰力矩系数迟滞环Fig.5 Hysteresis loops of pitching moment coefficient

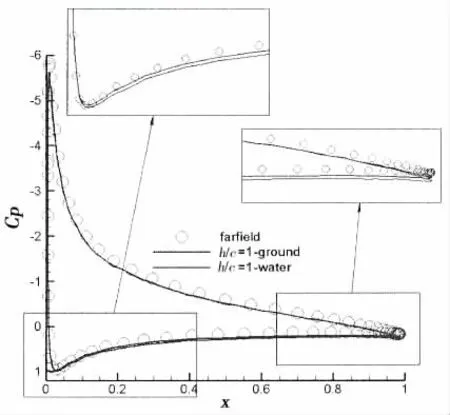
图6 三种模型物面压力系数 Fig.6 Pressure coefficients of three models

图7 自由空间压力云图Fig.7 Pressure contour of free flow field

图8 地面影响的压力云图Fig.8 Pressure contour of ground effect

图9 水面影响的压力云图Fig.9 Pressure contour of water surface effect

应用本文的动导数计算方法可以计算得到这三种情形下各个攻角的纵向俯仰力矩系数组合动导数，结果见图10，从图中可以看出近地/水高度相同的情况下，中小攻角时，受地面/水面的影响，动导数绝对值减小，动态稳定特性损失，且水面效应影响下的动导数绝对值减小得更为厉害，而在较大攻角时，这两种效应均能够增加动态阻尼，导致动导数绝对值的增大。究其原因，中小攻角时，受到翼型自身形状的影响，下翼面与地面/水面之间形成的通道表现出文丘里管效应，这种效应对通过管道的气流进行了加速，叠加上自身的非定常运动，致使翼型重心前后段的压力分布变化不再稳定，损失了整体的动态阻尼，地面由于呈现刚性，形成的管道效应一侧为平面，水面由于柔性作用易发生变形，形成的管道更为复杂，因而动导数绝对值也较地面影响时的小。大攻角时，这一情况刚好相反，下翼面与地面/水面形成的管道则以阻塞效应为主，非定常运动因为气流阻塞的影响而趋于减弱，也即系统的阻尼增大，因而动导数绝对值增大。

对比图10中的不同近地/水高度下的动导数变化，可知，随着h/c的增大，地面以及水面的动导数曲线都有着向自由空间结果靠拢的趋势，这表明两种效应的影响在减弱，而地面效应衰减得更快，在h/c=5时，其动导数随攻角变化曲线已经很接近自由空间结果，此时水面的影响依然很强，这也与之前的迟滞环变化一致。由此说明，在进行现代地效飞行器动态气动设计中，关于地面、水面以及自由空间的气动特性需要详细研究，区别对待。

图10 纵向组合动导数Fig.10 Longitudinal combined dynamic derivatives

6 结 论

根据对自由空间流场、地面以及水面影响下的流场的动态特性计算结果进行研究和分析，可以得出以下结论：

（1）本文建立的非定常方法能够较为准确地计算翼型运动时的非定常气动力及其迟滞效应，基于小幅度谐和振动的动导数辨识方法也能够精确地计算组合动导数。

（2）地面与水面的存在对于翼型的动态流场有着很大的影响，进而影响了翼型的动态阻尼，导致动导数绝对值的差异。但是地面的影响与水面不同。

（3）中小攻角下，地面与水面的影响均以管道效应为主，柔性的水面形成的效应使得翼型损失了更多的动态阻尼，动导数绝对值相比地面效应要小。

（4）大攻角时，影响动态特性的为阻塞效应，柔性水面的局部变形形成更为显著的恢复力矩以减弱非定常运动，因而动导数绝对值较地面的影响大。

（5）由于地面、水面影响的差异，在对近地、水面飞行器的动态气动特性进行研究时，要分别对待，细致分析不同条件下的流场特性。

[1]杨 美,杨 韡,杨志刚.地效翼地面粘性效应风洞试验研究[J].空气动力学学报,2015,33(1):82-86.Yang Mei,Yang Wei,Yang Zhigang.Wind tunnel test of ground viscous effect on wing aerodynamics[J].Acta Aerodynamica Sinica,2015,33(1):82-86.

[2]韩 龙,陈阳陵,王福新,等.高海况机翼波浪地面效应数值模拟与分析[J].上海交通大学学报,2014,48(8):1127-1133.Han Long,Chen Yangling,Wang Fuxin,et al.Numerical simulation and aerodynamic analysis of airfoil flying over wave ground at high grade sea condition[J].Journal of shanghai Jiaotong University,2014,48(8):1127-1133.

[3]盛其虎,吴德铭,张 亮.信天翁近海绵飞行时的气动力研究[J].应用数学和力学,2005,26(9):1114-1120.Sheng Qihu,Wu Deming,Zhang Liang.Aerodynamic forces acting on an albatross flying above sea-waves[J].Applied Mathematics and Mechanics,2005,26(9):1114-1120.

[4]邹光远,谭 华,张立柱.解极近水面飞行时全机气动力中水波效应的边界元法[J].水动力学研究与进展A辑,2003,18(4):379-396.Zou Guangyuan,Tan Hua,Zhang Lizhu.The boundary element method(BEM)solving the water wave effect on the aerodynamic of a vehicle flying close to water surface[J].Journal of Hydrodynamics Ser.A,2003,18(4):379-396.

[5]秦旭国,刘沛清,屈秋林,等.三维多段机翼地面效应数值模拟[J].航空学报,2011,32(2):257-264.Qin Xuguo,Liu Peiqing,Qu Qiulin,et al.Numerical simulation on 3D multi-element wings in ground effect[J].Acta Aeronautica et Astronautica Sinica,2011,32(2):257-264.

[6]秦旭国,刘沛清,屈秋林.翼型波浪水面巡航地面效应数值模拟[J].北京航空航天大学学报,2011,37(3):295-304.Qin Xuguo,Liu Peiqing,Qu Qiulin.Numerical simulation on aerodynamics of airfoil flying over wavy water surface[J].Journal of Beijing University of Aeronautics and Astronautics,2011,37(3):295-304.

[7]Chen Y S,Schweikhard W G.Dynamic ground effect on a two-dimensional flat plate[J].Journal of Aircraft,1985,22(7):638-640.

[8]Konstadinopoulos P,Thrasher D F,Mook D T,et al.A vortex-lattice method for general,unsteady aerodynamics[J].Journal of Aircraft,1985,22(1):43-49.

[9]Kornev N,Matveev K.Complex numerical modeling of dynamics crashes of wing-in-ground vehicles[J].AIAA 2003-600,2003.

[10]叶正寅,杨永年,陈迎春.有地面干扰的动导数计算方法[J].飞行力学,1998,16(3):68-72.Ye Zhengyin,Yang Yongnian,Chen Yingchun.Numerical calculation of dynamic stability derivatives in ground effect[J].Flight Dynamics,1998,16(3):68-72.

[11]Ronch A D,Vallespin D.Computation of dynamic derivatives using CFD[R].AIAA 2010-4817,2010.

[12]Jean-Francois L,Stephane M,Dominique F.Static and dynamic derivatives on generic UCAV without and with leading edge control[R].AIAA 2014-2391,2014.

Numerical simulation of aircraft dynamic stability characteristics flying over ground and water surface

MI Bai-gang,ZHAN Hao
(School of Aeronautics,Northwestern Polytechnical University,Xi’an 710072,China)

Based on unstructured dynamic mesh technique,SA turbulence model and volume of fluid(VOF)method,the 2-dimensional airfoil(NACA0012)unsteady aerodynamics flying over free flow field,ground and water surface were numerically studied,also the method to identify dynamic stability derivative was developed.It is shown that the method to calculate dynamic derivative is reliable.The absolute value of combined longitudinal dynamic derivative with water effect is the least at small angle of attack(AoA)as dynamic damping mostly decreases due to pipeline effect,which also happens on ground effect model,however,as the blockage effect at large AOA,both the dynamic stability of airfoil flying over ground and water surface are improved,besides,compared to ground,water affects a wider range to unsteady aerodynamics of airfoil.

free flow field;ground effect;water surface effect;dynamic derivative;numerical simulation;computational fluid dynamics(CFD)

V211.3

A

10.3969/j.issn.1007-7294.2017.11.004

1007-7294（2017）11-1348-08

2017-07-26

航空科学基金资助项目（2015ZA53013）；中央高校基本科研业务费专项资金资助项目（3102016HKJJ004

米百刚（1989-），男，博士研究生，E-mail：mibaigang@163.com；

詹 浩（1972-），男，教授，博士生导师。