首升力体、首鳍/尾板与船体水动力相互干扰与匹配研究
王习建,吴宝山,周德才,邱耿耀,高 雷,兰 波
(中国船舶科学研究中心,江苏 无锡 214082)
首升力体、首鳍/尾板与船体水动力相互干扰与匹配研究
王习建,吴宝山,周德才,邱耿耀,高 雷,兰 波
(中国船舶科学研究中心,江苏 无锡 214082)
升力体技术已被CFD、缩比模型试验和实船试验证实,在零航速与有航速情况下均可减小船舶在波浪中的运动响应,提高船舶耐波性。该文以数值计算为主要技术手段,结合模型试验验证,开展了首升力体、首鳍/尾板与船体水动力相互干扰与匹配研究。首先,采用自由船模拖曳的数值模拟方法,开展了基于快速性的首升力体与船体位置匹配研究,获得了首升力体在船体上的较佳位置;其次,对首升力体加装首鳍,分析了首升力体、首鳍组合与船体水动力相互干扰,获得了复合初步船型方案;再次,对复合初步船型方案加装尾板,讨论了首升力体、首鳍、尾板组合与船体水动力相互干扰,获得了复合优化船型方案;最后,对复合优化船型方案在规则波中的运动响应进行数值预报与对比分析,并预报不规则波中的减摇效果。文中的研究成果可为后续首升力体在单体船上的应用提供技术支撑。
首升力体;水动力相互干扰;运动响应
0 引 言
由于受到海风、海浪及海流等因素的影响,船舶在航行中会产生各种摇荡作用,剧烈的摇荡对船舶的适航性、安全性以及设备、人员的正常工作都会产生显著的影响。一直以来,人们都在寻求减小船舶摇荡,提高船舶耐波性的方法,并研制出了一些有效的船舶减摇装置[1]:舭龙骨、减摇鳍、减摇水舱、半潜首等。与此同时,在这过程中出现了许多优良船型,如小水线面双体船、半潜首船型、升力体船型等,这些船型都具有优良的耐波性[2]。
事实上,升力体技术已被CFD、缩比模型试验[3]和实船试验证实,在零航速与有航速情况下均可降低船舶运动,提高船舶耐波性。升力体是具有弧形横截面的水下结构物[4],具有较大的体积,较大的平面面积,以及低升力系数[5]。根据升力体的自身特点和在船体上的安装位置,可将升力体分为首升力体、中部升力体和尾升力体。如果将升力体与船的首部合理结合,不仅能减小船舶摇荡,提高船舶耐波性能,还有可能获得类似于球鼻首一样的积极作用[6],降低船舶阻力。
升力体技术转化为实船应用的首例是美国海军的“海飞”(Sea flyer)号舰艇[7](如图1所示),美国海军研究署和Navatek公司于2004年完成了“海飞”号舰艇的第一阶段技术演示任务。“海飞”号是一艘独特的升力体船,由于采用了升力体技术,它可在高航速的情况下将船体几乎完全抬出水面,并且仍具有较好的稳定性[8]。2006年,为了满足濒海战斗舰的使命要求,美国Navatek公司建造了BLB-70升力体技术示范艇(如图1所示),试验结果表明,与裸船体相比,BLB-70的升阻比提高了15%~30%,它不仅能降低船舶阻力,还能有效地减小船舶运动,这与CFD数值计算的结果十分吻合。但国内对升力体技术的研究成果尚未见公开发表。

图1 Sea flyer和BLB-70Fig.1 Sea flyer and BLB-70
目前,国外一些高性能船舶应用了升力体技术,主要利用升力体的抬升功能,将船体抬出水面,从而减小摩擦阻力,达到降低船舶总阻力目的。而作者主要利用首升力体与船体之间的有利波系干扰来减小船舶阻力,并提高船舶耐波性,而船体本身并不抬出水面。本文以CFD数值计算为主要技术手段,并结合水池模型试验方法,开展了基于快速性的首升力体、首鳍/尾板与船体之间的水动力干扰与匹配研究,获得了快速性和耐波性均优良的复合优化船型方案;最后,对复合优化船型方案开展了耐波性数值预报和模型试验,并评估其耐波性能。
1 数值计算方法
1.1 控制方程
不可压缩流体的连续性方程与动量守恒方程为:
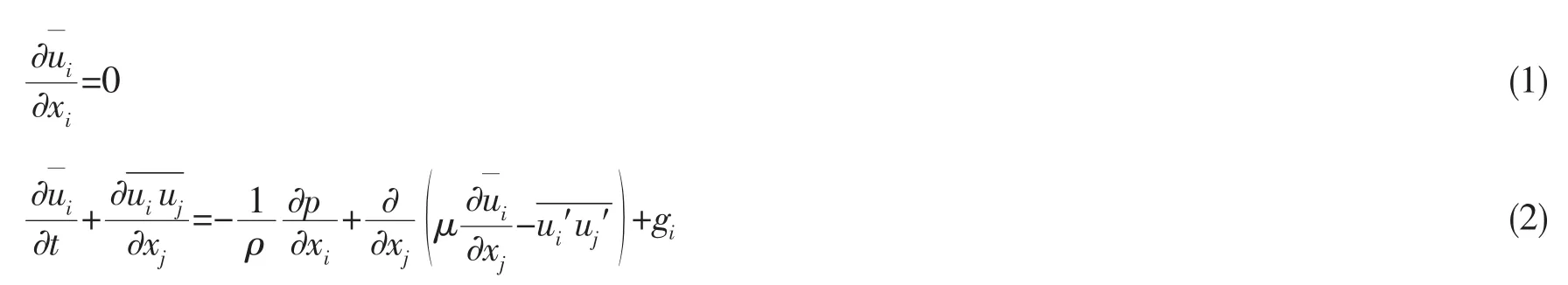
对于水面船自由面绕流这种两相流问题,水与空气的质量都应该是守恒的。由于流体的不可压缩性,可以用体积分数写为:

计算区域内的每个控制体积都由水或空气充满,它们的体积分数之和应为1,即:

式中:α表示体积分数,下标a和w分别代表空气和水。
1.2 湍流模型
本文所采用的湍流模型为RNG k-ε,此模型考虑了平均流动中的旋转及旋流流动情况,修正了湍动粘度和ε方程,这就使得RNG k-ε模型可以更好地处理高应变率及流线弯曲程度较大的流动。
湍流动能k的方程为:
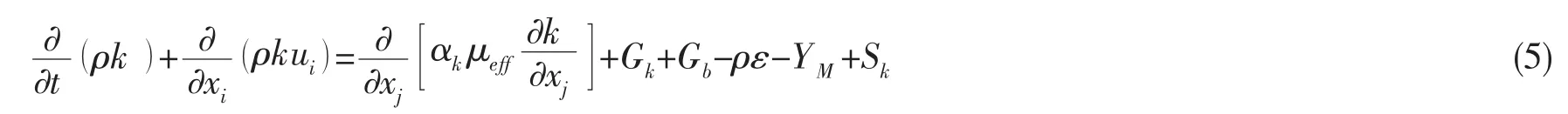
湍流耗散率ε的方程为:
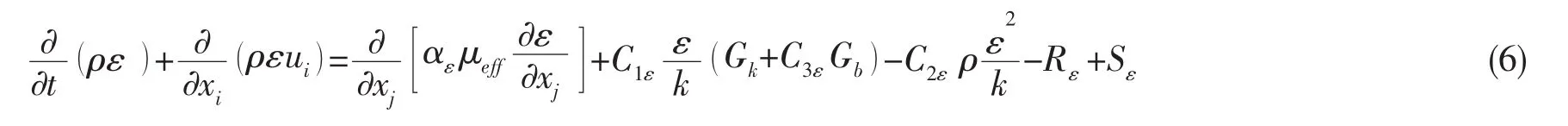
式中:C1ε=1.42,C2ε=1.68。
1.3 造波与消波
采用在入口边界模拟柔性造波板运动的速度分布产生入射波。根据深水中的线性波浪理论,规则波的自由波面可以表达成[9]:

而规则波的速度场为:

式中:A是波幅,k为波数,ω是波浪圆频率;x轴为波浪传播方向,z轴为波动方向。
数值消波采用网格技术结合人工阻尼的方法,消波区人工阻尼Dmp的表达式:

1.4 船体运动与流动的耦合
水面船模拖曳前进时,会对其周围流场产生影响,使压力场和剪应力场发生变化,也就使船模所受的力和力矩发生变化:

2 首升力体与船体水动力相互干扰与匹配研究
2.1 光体及首升力体主尺度
众所周知,深V船型自问世以来,就因为其在波浪中的良好性能而备受研究人员青睐。本文以千吨级深V船型作为研究对象,参考相关文献[10],并对其型线进行了适当改型。选取水线长L=4 m的模型作为计算对象,模型主尺度见表1,横剖面型线见图2。

表1 模型主尺度Tab.1 Main dimensions of scale model
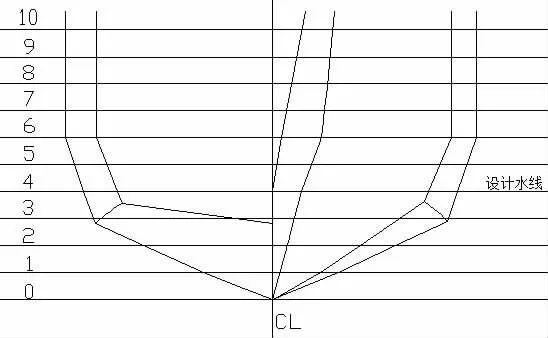
图2 横剖面型线图Fig.2 The body section of bare hull

图3 首升力体三维效果图Fig.3 Three-dimensional sketch of bow-lifting-body
通过对有自由液面情况下,不同长宽比、不同浸深和不同航速首升力体水动力特性的研究,综合考虑首升力体的升阻比、自由面兴波和结构强度等因素,选取长宽比λ=2的首升力体为研究对象,三维效果图见图3,模型尺度见表2。

表2 首升力体模型尺度Tab.2 Model dimensions of the bow-lifting-body
2.2 首升力体纵向位置研究
针对选取的光体和首升力体,开展首升力体与船体位置匹配研究。首升力体在船体上的布置主要考虑纵向位置和垂向位置,首先对首升力体的纵向位置进行匹配研究。

图4 首升力体纵向位置方案Fig.4 The longitudinal position scheme of bow-lifting-body
为了获得首升力体相对于船体的最佳纵向位置,以水线和船体首柱的交点A作为起始位置,将首升力体分别后移0.5站,前移0.5站、1站、1.5站、2站,对6个不同首升力体纵向位置方案,见图4,在航速V=2.025 m/s(Fr=0.32)和 V=3.372 m/s(Fr=0.54)下进行静水自由模[11]CFD阻力数值计算,并与光体自由模CFD阻力数值计算结果进行比较分析,见图5。
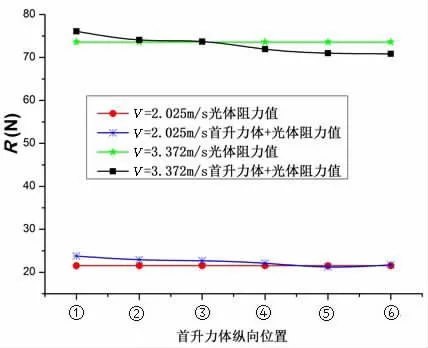
图5 不同首升力体纵向位置阻力计算值Fig.5 Resistance calculation results of bow-lifting-body at different location
图5给出了首升力体处于不同纵向位置的阻力计算结果,从图中可以看出,当航速为 2.025 m/s(Fr=0.32),首升力体处于①、②、③、④位置时,复合船型阻力均大于光体,而当首升力体处于⑤、⑥位置时,复合船型阻力均小于光体,⑤位置时复合船型阻力最小,此时阻力较光体降低1.39%。当航速为 3.372 m/s(Fr=0.54),首升力体处于①、②、③位置时,复合船型阻力均大于光体,随着首升力体继续前移,④位置时复合船型阻力开始小于光体,当首升力体处于⑤位置时,复合船型阻力降低3.51%,而当首升力体处于⑥位置时,复合船型阻力最小,较光体降低3.71%。基于以上分析,首升力体前移将会降低复合船型阻力,但是考虑到工程实际应用,如果首升力体前移过多,将会导致全船长度增加,这会带来一些其他的问题,比如船舶进坞、回转等将受到较大的影响;同时,还会影响到首升力体与船体连接的结构强度。综合考虑这些因素,选取首升力体处于⑤位置,即首升力体前移1.5站时作为首升力体纵向位置最佳方案。
2.3 首升力体垂向位置研究
在纵向位置匹配方案的基础上,对首升力体的垂向位置进行匹配研究,首先对首升力体在不同浸深时自由面兴波的波形进行了数值计算。
图6为不同浸深时首升力体自由面中心线处波高的比较(其中H为首升力体前缘点到水面的距离,L为首升力体的最大弦长),从图中可以发现,首升力体的浸深比越小,波幅越大,产生的兴波越明显,这将有助于利用首升力体产生的兴波与船首产生的兴波发生有利波系干扰,起到降低船舶阻力的作用,因而首升力体的垂向位置不应太深;但若浸深太浅,首升力体会产生出水现象,对结构强度造成损坏,为此垂向位置选取首升力体弦长位置与船体基线齐平,这与常规球鼻首在船体上的垂向位置布置相一致。同时考虑到首升力体与船体连接支柱形式的阻力和结构强度等因素,首升力体与船体匹配位置,见图7。
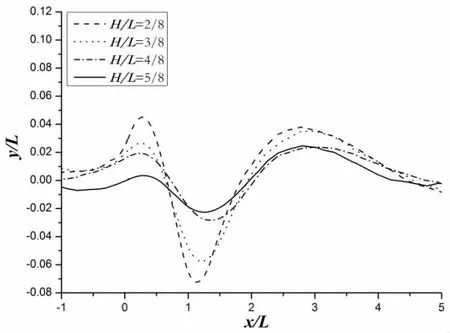
图6 不同浸深时首升力体自由面处的波高Fig.6 Wave height of free surface under different depth

图7 首升力体与船体匹配方案Fig.7 Matching scheme of bow-lifting-body and monohull
3 首升力体、首鳍/尾板组合与船体水动力相互干扰与匹配研究
通过对首升力体加装首鳍,研究首升力体、首鳍组合与船体的水动力相互干扰,获得了复合初步船型方案,然后在船体上加装尾板,进行了船体航行姿态调整与优化,研究首升力体、首鳍、尾板组合与船体的水动力相互干扰,探索首升力体的减阻效果,并获得了复合优化船型方案。
3.1 首升力体、首鳍组合与船体水动力干扰特性分析
(1)首鳍与首升力体几何构型
为了更好地改善船舶耐波性,在首升力体上加装首鳍,这样可以提高船体纵向运动性能。考虑到减纵向运动的效果,选取的首鳍尺寸不宜太小;但若首鳍的尺寸过大,将会引起首升力体阻力的大幅增加,还会增加首升力体宽度,导致船舶回转、进港受限等,同时带来结构强度问题。基于这些因素的考虑,加装首鳍后的首升力体,见图8。
(2)复合初步船型方案快速性数值计算
对加装首升力体、首鳍的复合初步船型方案V1,进行静水中船体航行姿态和阻力计算,并与试验值对比,验证了数值计算方法,见图10~12。其中V为对应速度,Z为升沉值,θ为纵倾角(尾倾为正),R为阻力值。

图8 加装首鳍后的首升力体Fig.8 The bow-lifting-body with fin

图9 加装首升力体、首鳍的复合初步船型方案(V1船型)Fig.9 The preliminary scheme of hybrid monohull with bow-lifting-body and fin
图10升沉曲线计算结果表明,光体、V1船型的升沉值随航速增加先减小后增大,由于加装了首升力体、首鳍,V1船型的升沉值大于光体。图11纵倾曲线计算结果表明,光体、V1船型的纵倾值随航速增加逐渐增大,当航速为3.707 m/s(Fr=0.59)时,由于首升力体的升力作用,V1船型航行纵倾角达到1.8°,大于光体的纵倾角,航行姿态变差,导致V1船型的静水阻力大于光体。由图12静水阻力数值计算结果可知,V1船型静水阻力在低速时略大于光体,随着航速的增加,逐渐与光体接近,当航速大于2.025 m/s(Fr=0.32)时,小于光体阻力,此时首升力体、首鳍组合起到了减阻的作用,当航速为3.037 m/s(Fr=0.48)时,V1船型减阻最大,约为 7%。

图10 静水中升沉曲线图Fig.10 Sinkage in still water
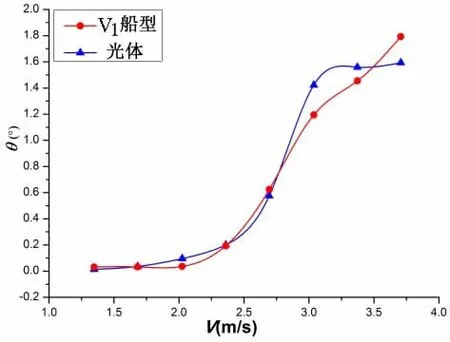
图11 静水中纵倾曲线Fig.11 Trim in still water
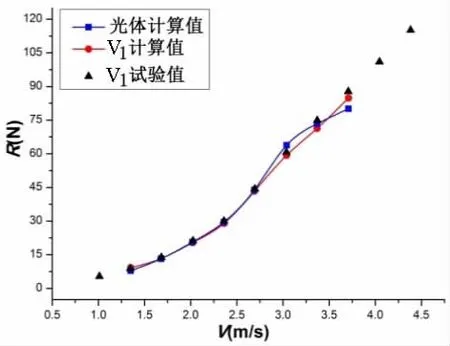
图12 阻力计算结果Fig.12 Calculation results of resistance
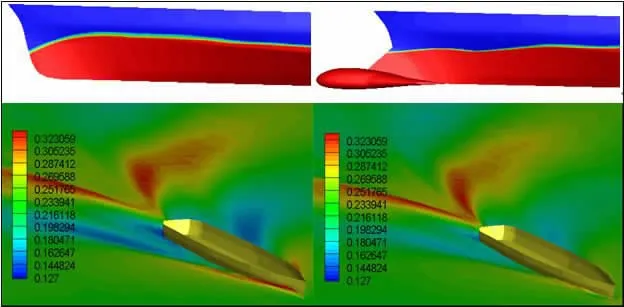
图13 首升力体消波效果图Fig.13 Wave cancellation sketch of bow-lifting-body
图13为航速V=3.372 m/s(Fr=0.54)时,光体和V1船型的首部波形图,从图中可以看出,由于加装了首升力体、首鳍,V1船型首部的兴波被显著地削弱了,首部兴波得到明显改善,从直观上解释了V1船型阻力减小的原因。
(3)复合初步船型方案阻力特性分析
通过对光体和V1船型阻力成份比较,进一步分析首升力体、首鳍组合减阻的原因。
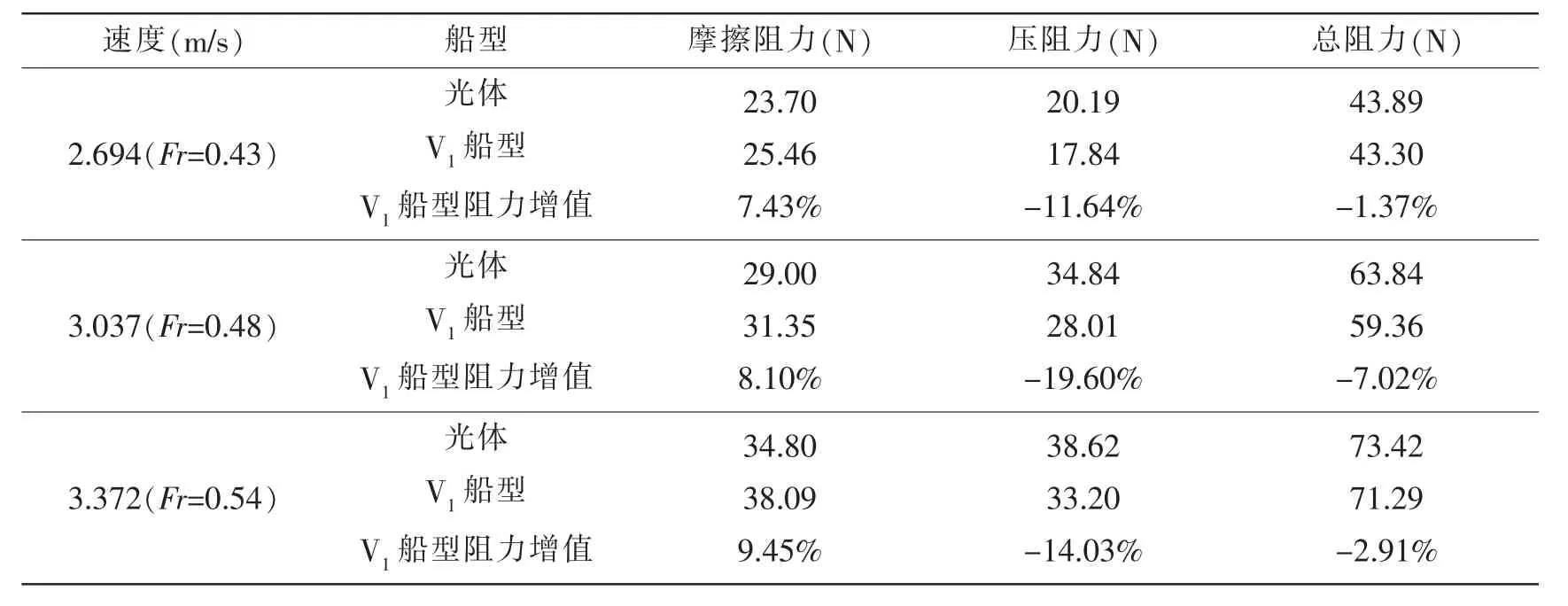
表3 阻力成份分析Tab.3 Analysis of resistance component
对3个航速下光体、V1船型的阻力成份进行分析,从表3中可以看出,由于加装了首升力体、首鳍,V1船型的摩擦阻力明显大于光体;从压阻力的减小可以看出,首升力体、首鳍组合与船体发生了有利波系干扰,起到了减小压阻力的作用。对于总阻力而言,由于V1船型压阻力的减小量大于摩擦阻力的增加量,首升力体、首鳍组合起到了减小船体总阻力的效果。
3.2 首升力体、首鳍、尾板组合与船体水动力干扰特性分析
根据上文的分析可知,当V1船型航速为3.707m/s(Fr=0.59)时,其总阻力明显大于光体,主要是因为此时首升力体、首鳍组合对V1船型首部抬升力过大,导致V1船型航行姿态变差。因而,需要对复合初步船型方案进一步优化。

图14 加装首升力体、首鳍和尾板的复合优化船型方案(V2船型)Fig.14 The optimization scheme of hybrid monohull with bow-lifting-body,fin and stern flap
通过安装尾板来平衡由首升力体和首鳍产生的升力,调整船舶姿态,降低其阻力。参考相关研究成果[12],选取尾板弦长为水线长的2%,展长与尾封板宽度相同,为达到较好的压浪效果和避免使船体出现较大的埋首,优化后选取尾板下反角α=5°,如图14所示。
(1)复合优化船型方案快速性数值计算
对加装首升力体、首鳍和尾板的复合优化船型方案V2,进行静水中船体航行姿态和阻力计算,并与试验值对比,验证了数值计算方法,见图15~17。
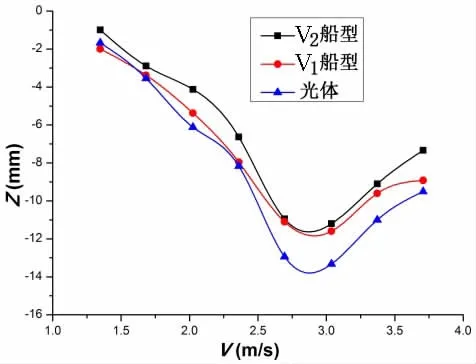
图15 静水中升沉曲线 Fig.15 Sinkage in still water
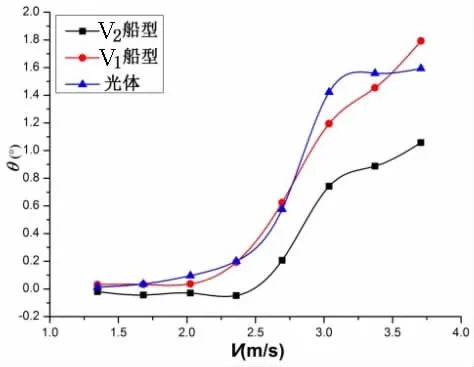
图16 静水中纵倾曲线Fig.16 Trim in still water
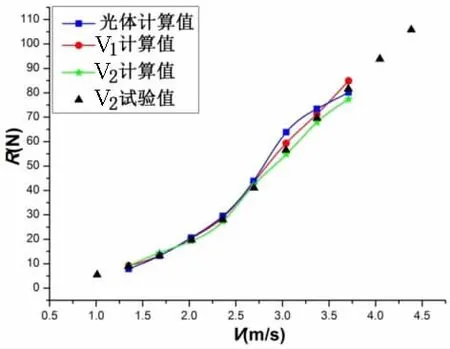
图17 阻力计算结果Fig.17 Calculation results of resistance
图15升沉曲线计算结果表明,首升力体、首鳍和尾板三者组合提供了升力,使得V2船型的升沉值最小。同时,图16纵倾曲线计算结果表明,V2船型纵倾值明显小于光体、V1船型,这表明尾板很好地平衡了首升力体的抬首力矩,调整了船舶航行姿态,使船舶抬首显著减小。由图17静水阻力数值计算结果可知,在低航速时,由于加装了首升力体、首鳍和尾板,V2船型静水阻力大于光体和V1船型。在中、高航速时,V2船型阻力最小,当航速为3.037 m/s(Fr=0.48)时,与光体相比,V2船型减阻最大,约为14%;与V1船型相比,加装尾板的V2船型在航速大于2.025 m/s(Fr=0.32)时,体现出了更好的静水阻力性能,这表明首升力体、首鳍和尾板三者的匹配较为成功。
(2)复合优化船型方案阻力特性分析
通过对V1船型和V2船型阻力成份比较,分析V2船型的阻力特性。
对3个航速下V1船型、V2船型阻力成份进行分析,从表4中可以发现,加装尾板后,尽管增加了V2船型的摩擦阻力,但尾板改善了船舶航行姿态,使V2船型压阻力进一步减小,由于压阻力的减小量大于摩擦阻力的增加量,从而降低了总阻力。此外,由试验现象和数值计算结果可知,尾板的安装在一定程度上也减小了船舶阻力。
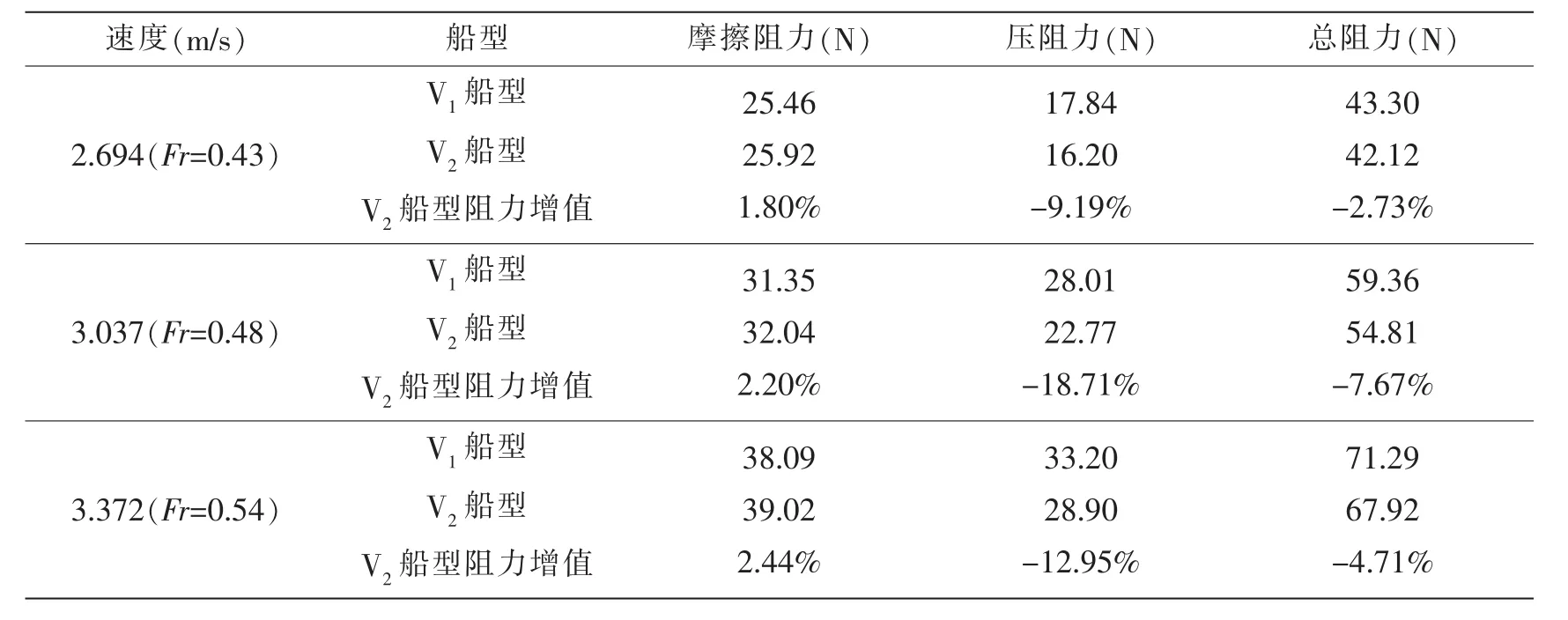
表4 阻力成份分析Tab.4 Analysis of resistance component
4 复合优化船型方案耐波性预报
由前文CFD快速性数值计算结果可知,加装首升力体、首鳍和尾板的复合优化船型方案V2具有良好的静水阻力性能,下面基于CFD数值波浪水池和耐波性模型试验,对复合优化船型方案在规则波中的运动响应进行数值预报与对比分析,并预报不规则波中的减摇效果。
4.1 规则波中运动响应数值计算预报与模型试验
对光体、复合优化船型方案V2在V=2.025 m/s(Fr=0.32)和V=2.694 m/s(Fr=0.43)两个航速下进行顶浪规则波中运动响应数值计算,预报了纵摇,垂荡以及首部19站、重心、尾部1站处垂向加速度,并对V2船型开展耐波性模型试验。图18为规则波中运动响应数值预报与模型试验结果。其中,λ为波长,L为设计水线,Z为垂荡值,ξ为波幅,θ为纵摇角,k为波数,A1为首部加速度,A2为重心加速度,A3为尾部加速度,g为重力加速度。
从图18中可以看出,两个航速下纵摇运动响应的CFD数值计算结果与试验值吻合较好;垂荡运动响应、首部19站、重心和尾部1站处垂向加速度运动响应的数值计算结果与试验值也吻合较好,但总体上数值计算结果要略大于试验值。
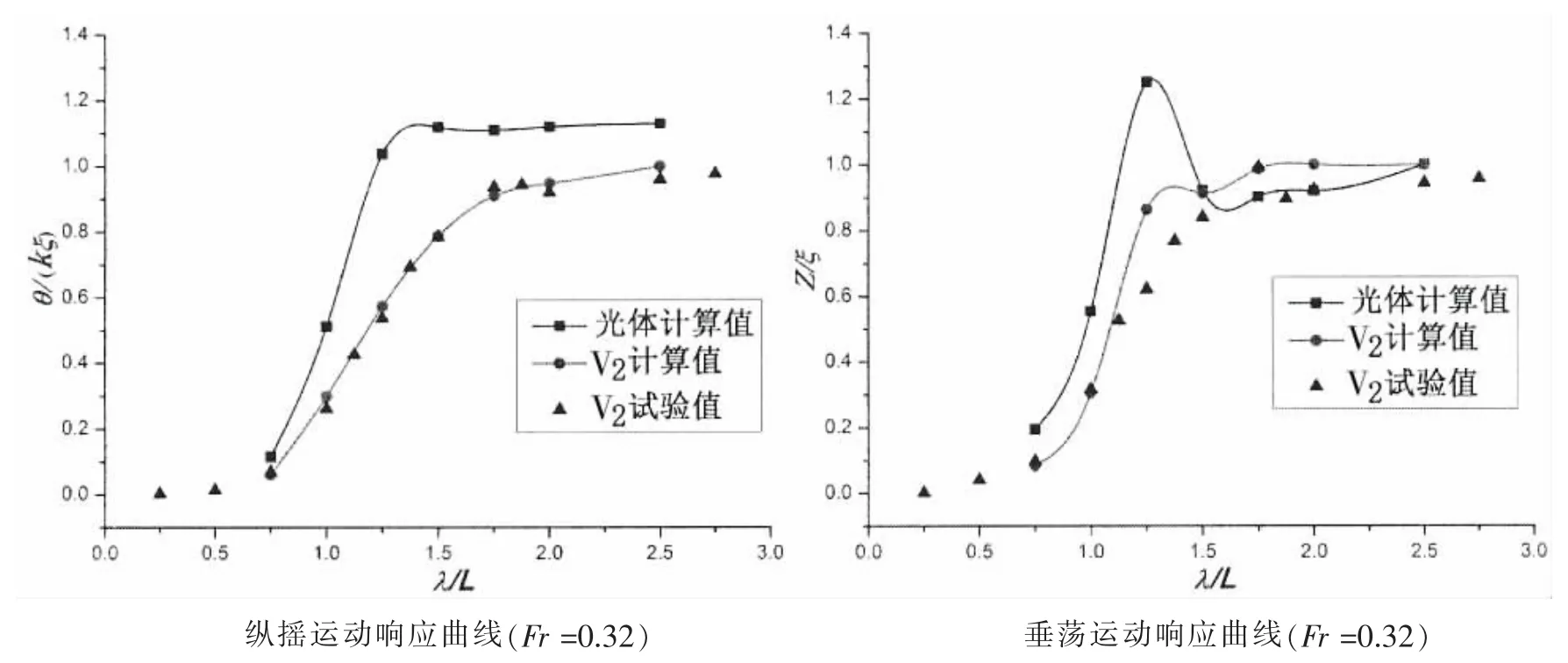
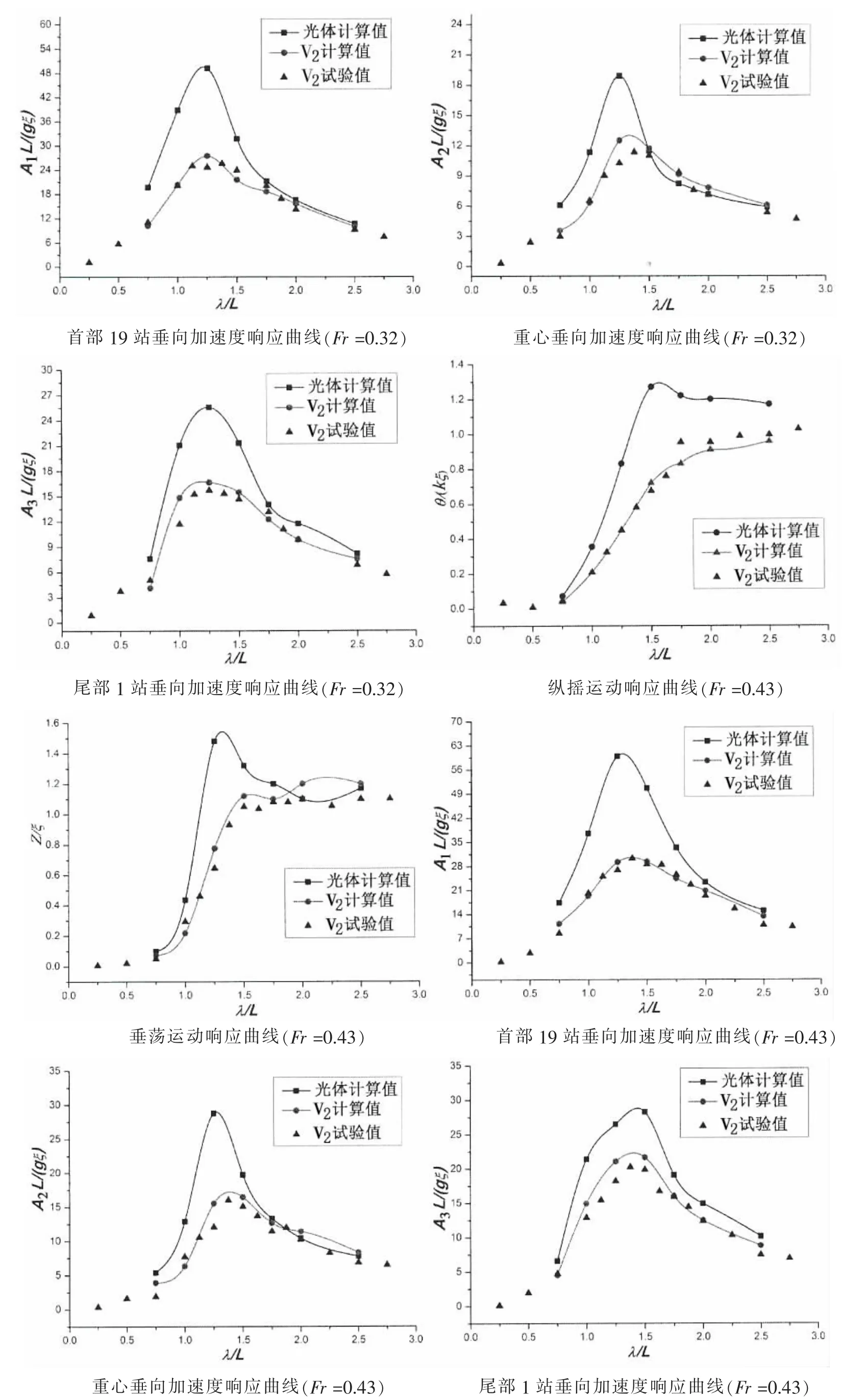
图18 规则波中运动响应数值预报与模型试验结果Fig.18 Numerical prediction of motion response in regular wave and model test results
从图18的运动响应曲线可以看出,与光体相比,复合优化船型方案的纵向运动响应明显减小,表明加装首升力体、首鳍和尾板后,复合优化船型方案产生了较大的纵向力矩,对船舶的纵向运动起到了很好的抑制作用。特别是,当波长在0.75~1.5倍船长时,复合优化船型方案的减摇效果最为明显。
4.2 不规则波中运动有义值预报
根据规则波中的运动响应传递函数和线性叠加原理,对光体和V2船型采用ITTC双参数谱,预报了有义波高分别为2.5 m、4 m和6 m,在航速18 kns和24 kns下的运动响应有义值,见表5,并分析了复合优化船型方案V2与光体相比的纵向减摇效果,见表6。
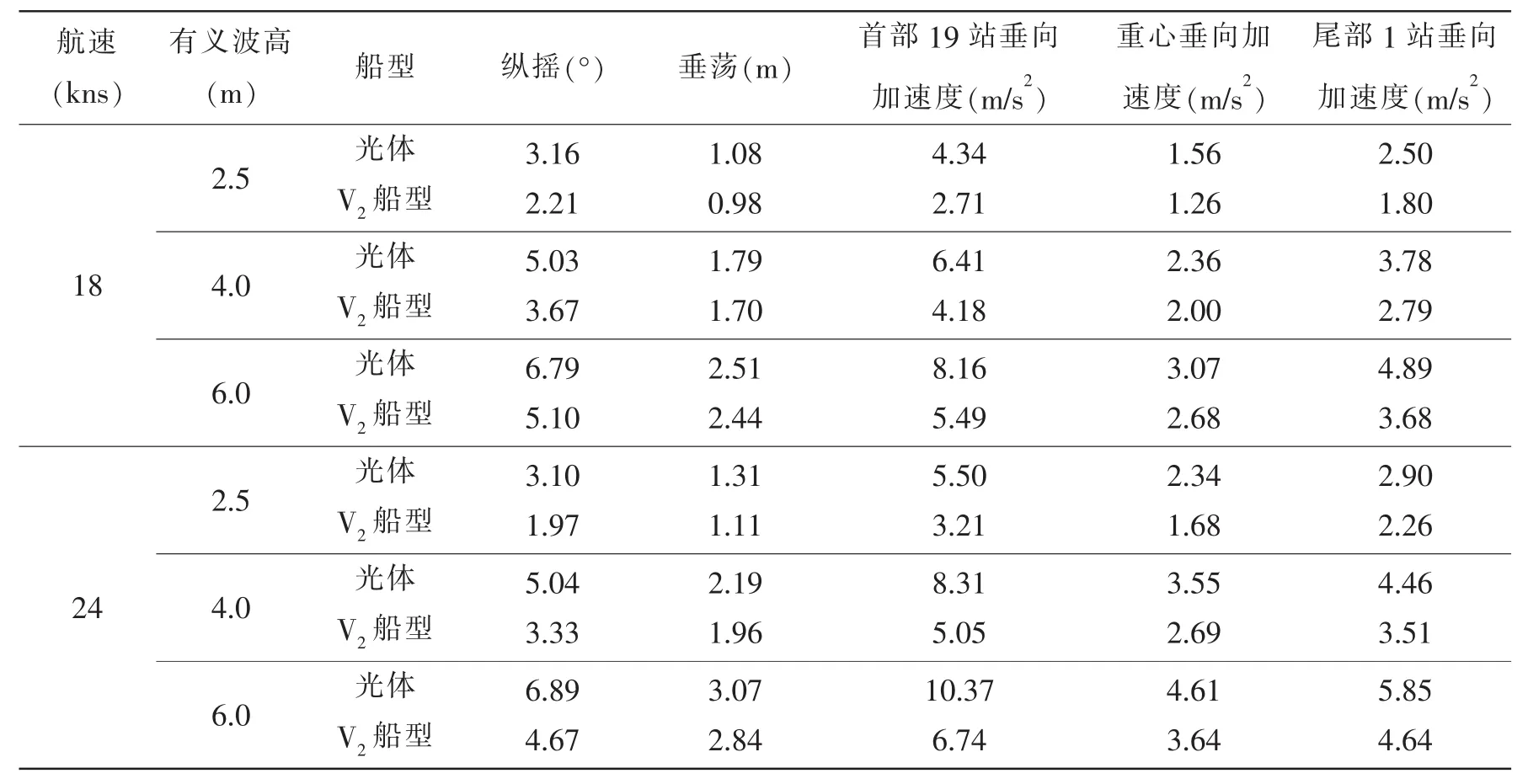
表5 不规则波中运动响应(单幅有义值)Tab.5 Motion response in irregular waves
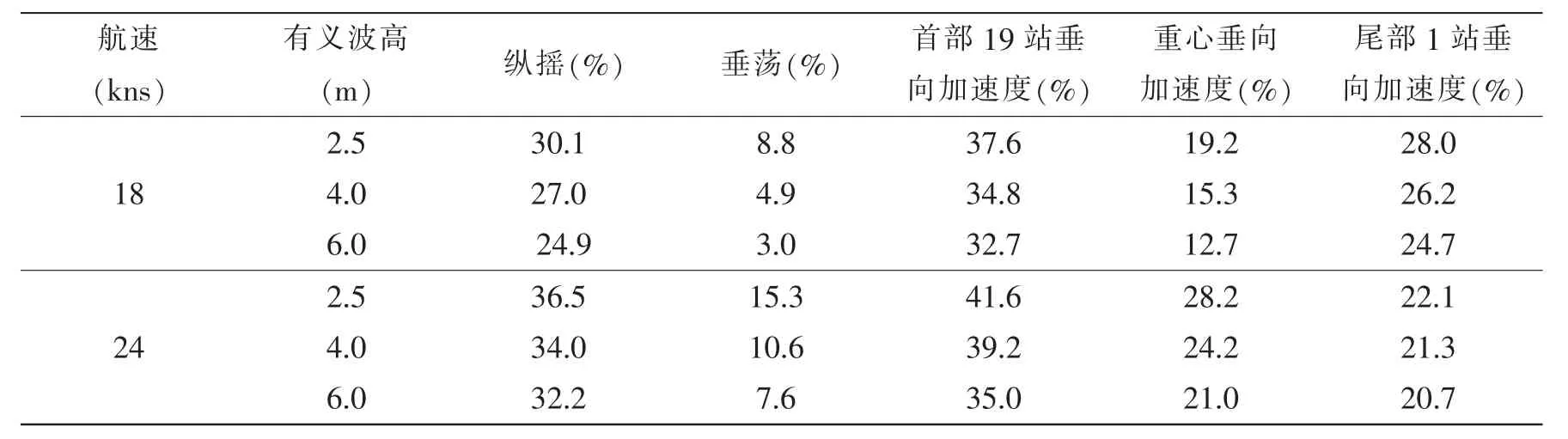
表6 复合优化船型方案减摇效果Tab.6 The stabilizing effect of optimization scheme
从表6可见,在不同有义波高下,复合优化船型方案V2的运动响应明显小于光体;航速18kns时,纵摇运动平均减摇效果为27.3%,垂荡运动平均减摇效果为5.6%,首部19站垂向加速度,重心垂向加速度,尾部1站垂向加速度平均减摇效果为35.0%,15.7%,26.3%;航速24kns时,纵摇运动平均减摇效果为34.2%,垂荡运动平均减摇效果为11.2%,首部19站垂向加速度,重心垂向加速度,尾部1站垂向加速度平均减摇效果为38.6%,24.5%,21.4%。可以发现,航速越高,V2船型的减摇效果越明显。
5 结 语
本文以数值计算为主要技术手段,开展了基于快速性的首升力体、首鳍/尾板组合与船体之间的水动力干扰与匹配研究,获得了快速性和耐波性均优良的复合优化船型方案,得到主要结论如下:
(1)加装首升力体、首鳍/尾板后,尽管增加了湿表面积,增大了复合船型摩擦阻力,但通过利用首升力体、首鳍/尾板组合与船体之间的有利波系干扰和有效匹配,减小了复合船型的压阻力,最终降低了复合船型的总阻力,与光体相比,复合初步船型方案减阻最大可达7%,复合优化船型方案减阻最大可达14%;
(2)加装首升力体、首鳍和尾板复合优化船型的耐波性能明显优于光体,波长在0.75~1.5倍船长时,纵向减摇效果最为明显;且航速越高,复合优化船型方案V2的减摇效果越明显。本文的研究成果可为后续首升力体在单体船上的应用提供技术支撑。
[1]洪 超,陈莹霞.船舶减摇技术现状及发展趋势[J].船舶工程,2012(S2):236-244.Hong Chao,Chen Yingxia.Current situation and tendency of development of ship stabilizer technique[J].Ship Engineering,2012(S2):236-244.
[2]Hart C J,Weems K M,Peltzer T J.Seakeeping analysis of the lifting body technology demonstrator sea flyer using advanced time-domain hydrodynamicsC]//Ninth International Conference on Fast Sea Transportation.Shanghai,China,2007.
[3]Hackett J P,Pierre J C S,Bigler C,et al.Computational predictions vs.model testing for a high speed vessel with lifting bodies[J].Transactions-Society of Naval Architects and Marine Engineers,2007,115:163-180.
[4]Loui S,Shimozono G,Keipper T.Low drag submerged asymmetric displacement lifting body:U.S.Patent 7,004,093[P].2006-2-28.
[5]Navatek,ltd.Lifting body technology for transformational ship designs[C].9th Naval Platform Technology Seminar,2003.
[6]Peltzer T J,Keipper T S,Kays B,et al.A new paradigm for high-speed monohulls:the bow-lifting-body ship[C]//Proceedings,Ninth International Conference on Fast Sea Transportation.Shanghai,China,2007.
[7]赵连恩,谢永和.高性能船舶原理与设计[M].第一版.北京:国防工业出版社,2009.
[8]Engle A,Lien V,Hart C.Seakeeping evaluation and loads determination of a high-speed hull form with and without a bow-lifting-body[J].FAST,2011.
[9]吴乘胜,朱德祥,顾 民,等.数值波浪水池及顶浪中船舶水动力计算[J].船舶力学,2008,12(2):168-179.Wu Chengsheng,Zhu Dexiang,Gu Min,et al.Computation of hydrodynamic forces for a Ship in regular heading waves by a viscous numerical wave tank[J].Journal of Ship Mechanics,2008,12(2):168-179.
[10]王许洁,孙树政,赵晓东,等.千吨级高耐波性单体复合船型模型试验研究[J].船舶力学,2011,15(4):180-187.Wang Xujie,Sun Shuzheng,Zhao Xiaodong,et al.Research on model test of thousands-tons class high seakeeping performance hybrid monohull[J].Journal of Ship Mechanics,2011,15(4):180-187.
[11]吴乘胜,陈 雄,孙立宪,等.静水中自由船模拖曳CFD模拟方法研究[J].船舶力学,2010,14(8):823-833.Wu Chengsheng,Chen Xiong,Sun Lixian,et al.Numerical simulation of free ship model towed in still water[J].Journal of Ship Mechanics,2010,14(8):823-832.
[12]邵世明,王云才.尾压浪板对高速艇阻力性能的影响[J].中国造船,1981,1:31-41.Shao Shiming,Wang Yuncai.The effects of stern trimming flap on resistance of high speed craft[J].Shipbuilding of China,1981,1:31-41.
Research on hydrodynamic interaction and matching of bow-lifting-body,fin/stern flap and hull
WANG Xi-jian,WU Bao-shan,ZHOU De-cai,QIU Geng-yao,GAO Lei,LAN Bo
(China Ship Scientific Research Center,Wuxi 214082,China)
Lifting body technology was demonstrated-via computational fluid dynamics,scale-model tests,and full-scale at-sea trials-to provide reduced motions at zero and loiter speeds,which can improve ship seakeeping performance.With numerical calculation and scale-model test verification,this paper makes a research on hydrodynamic interaction and matching of bow-lifting-body,fin/stern flap and hull.The numerical simulation method of free ship model towed in still water is adopted.Research on position between bow-lifting-body and hull is carried out and the better position is obtained.With the fin installed on the bow-lifting-body,hydrodynamic interaction of bow-lifting-body,fin and hull is analysed.And the preliminary scheme of hybrid monohull is obtained.With the stern flap installed on the preliminary scheme,hydrodynamic interaction of bow-lifting-body,fin,stern flap and hull is discussed.And the optimization scheme of hybrid monohull is obtained.Finally,numerical prediction of motion responsein regular waves and comparative analysis of the optimization scheme are carried out.The stabilizing effect of hybrid monohull is also predicted.The results in the paper can be applied to the research of monohull with bow-lifting-body in the future.
bow-lifting-body;hydrodynamic interaction;motion response
U661.1
A
10.3969/j.issn.1007-7294.2017.11.003
1007-7294(2017)11-1336-12
2017-05-23
王习建(1990-),男,硕士,工程师,E-mail:380678482@qq.com;
吴宝山(1968-),男,博士,研究员。
——福船

