低速水面目标航速精度分析及精确解算

苗高洁

(江苏自动化研究所，江苏 连云港 222061)

0 引 言

航速指目标单位时间内运动的距离，是描述目标运动的基本要素之一。在实际应用中，除了多普勒雷达等少数雷达之外，绝大多数雷达不能提供目标航速的直接测量信息，而是通过航迹滤波间接获取。因此，航速精度主要取决于目标位置测量精度，与目标本身航速大小基本没有关系。低速水面目标由于在雷达扫描周期内运动距离较小，受雷达测量精度的限制，导致通过航迹滤波输出的航速误差相对目标航速而言往往较大。而且对于同样的航速误差，目标航速越小航速误差比越大，以至于当目标航速较小时，滤波输出的航速几乎不可用。

针对低速水面目标航速解算问题，袁桂生[1]在介绍了海空目标相对和绝对航速解算方法的基础上，探讨了几种提高航速解算精度的途经，但不够深入；黄孟俊等[2]提出一种海上目标航向航速解算新方法，利用雷达载体的精确GPS信息实现海上目标航向航速的高精度解算；韩孟孟等[3]研究了一种多站模式下舰船航向航速快速解算方法，提高了航向航速解算速率，并未提高解算精度。因此为了提高低速水面目标航速解算精度，本文在分析航速精度影响因素的基础上，提出一种基于两级策略的航速精确解算方法，并通过仿真试验验证了算法的有效性。

1 航速精度分析

依据目标航速的定义，有

由于雷达测量存在误差，获得的目标位置参数实际应为

因此，实际获得的航速为

于是航速误差为

其中

因此航速误差为

下面依次分析距离、方位、俯仰各测量误差对航速精度的影响。

1.1 距离误差影响

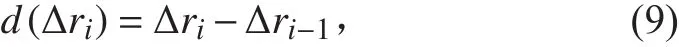
从而可得距离误差对航速精度的影响为

1.2 方位误差影响

从而可得到方位误差对航速精度的影响为

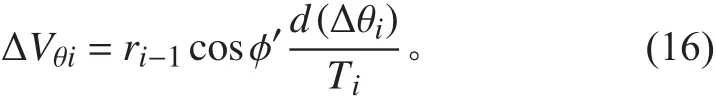
1.3 俯仰误差影响

从而可得俯仰误差对航速精度的影响为

2 航速精确解算

通过以上分析可得，欲减小距离、方位、俯仰各测量误差对航速精度的影响，均需要增加。但不能太大，因为前面的分析基于目标直线运动这样一个假定前提。当较小时，这样的假定没有问题，即使目标并不是直线运动（如图1中虚线L1），但当较大时，这样的假定可能明显失真（如图1中虚线L2）。

为了克服这个困难，本文采用两级解算策略。如图2所示，首先选取较小的（比如2个测量周期）计算相应的，以取得较好的直线近似性能；然后再对最近的个进行平滑处理，等效于取得较大的。

均值漂移（Mean Shift)算法是一种在一组数据的概率密度分布中寻找局部极值稳定的方法，具有良好的平滑效果，同时还能适应一定的变化[4–6]。因此采用mean shift算法对进行平滑处理。步骤如下：

图1 周期大小对直线近似的影响Fig.1 The effect of the periodic size on the linear approximation

图2 基于两级策略的航速精确解算示意图Fig.2 Accurate calculation of speed based on two-level strategy

②计算核函数

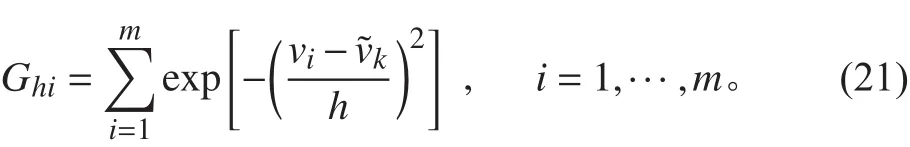
③计算mean shift值

3 仿真验证

下面设置3个典型的场景对算法进行仿真验证。仿真中，雷达探测周期为2 s，距离探测精度为100 m，方位探测精度为0.3°。

场景1：平台以6 m/s的航速向正北运动，目标初始相距平台约30 km，以10 m/s的航速匀速直线向正东运动。

场景2：平台以6 m/s的航速向正北运动，目标初始相距平台约30 km，开始以10 m/s的航速匀速直线向正东运动，期间一段时间减速运动。

场景3：平台以6 m/s的航速向正北运动，目标初始相距平台约30 km，开始做转弯运动，之后以10 m/s的航速匀速直线向正东运动。

通过航速精确解算得到精算前后航速对比结果，分别如图3、图4和图5所示。精算前航速指雷达上报的航速，精算后航速指采用本文算法精确解算得到的航速。

图3 目标1精算前后航速对比结果Fig.3 Speed comparison result before and after the accurate calculation of target 1

图4 目标2精算前后航速对比结果Fig.4 Speed comparison result before and after the accurate calculation of target 2

图5 目标3精算前后航速对比结果Fig.5 Speed comparison result before and after the accurate calculation of target 3

统计精算前后的航速误差，如表1所示。

表1 精算前后航速误差Tab.1 Speed error before and after accurate calculation

从仿真验证结果可以看出：该算法能够大幅提高航速精度（见表1），并且有效抑制原航速信息中存在的毛刺现象（如图3～图5所示）。

4 结 语

针对低速水面目标航速解算问题，本文首先从理论角度分析了航速精度的影响因素，发现距离、方位、俯仰测量误差中的变化部分是影响航速精度的主要因素，要降低其影响需要增大解算周期。然后根据分析结果设计了基于两级策略的航速精确解算方法，单次解算时适度增大解算周期，以取得较好的直线近似性能，在此基础上对多个单次解算结果进行平滑处理，以达到进一步增大解算周期的效果。最后通过仿真试验对算法进行验证，结果表明本文算法在提高航速精度等方面具有明显效果。