不同边界条件薄壁截锥壳的高阶振动特性研究
杨志宏,李 昊,孟强强,夏 鑫,王 宇,于晓光
(辽宁科技大学 机械工程与自动化学院,辽宁 鞍山114051)
薄壁构件通常是厚度与结构件最小平面跨度之比在1/80和1/5之间的弹性构件[1-2]。薄壁截锥壳结构广泛应用于航空航天和船舶等诸多领域。由于其工作环境较为恶劣,薄壁截锥壳结构的振动行为复杂,例如在高转速或外部复杂载荷条件下,易产生高阶共振和失稳等现象。对薄壁截锥壳的高阶振动特性进行研究,在构件的设计和故障诊断中具有重要的应用价值。
关于薄壁截锥壳的振动问题已有大量研究,但是大部分都集中于低阶振动特性的研究,对薄壁截锥壳的高阶振动特性研究较少。Shu等[3]提出一种微分求积的全局方法分析锥壳的振动问题,但求解误差较大。Caresta等[4]在外载荷下分析了截锥壳低阶振动特性。Bagheri等[5]采用Donnell壳体理论,在考虑连续性条件的基础上,将壳体分为两部分,研究了带中间环支撑壳体的振动问题。Jin等[6]采用一种改进的傅里叶级数法,对一般边界条件下截锥壳进行了研究。Kouchakzadeh等[7]基于Donnell壳体理论和Hamilton原理,求解出圆柱-板等组合壳体的固有频率。Wang等[8]基于传递矩阵法和有限元仿真,分析了不同边界条件下篦齿对薄壁圆柱壳固有频率的影响。Ma等[9]通过瑞利-里兹法求解了组合壳体低阶固有频率。任红军等[10]采用瑞利-里兹法分析了中心固支条件下薄壁圆盘的振型特性。江滨等[11]在Love壳体理论的基础上,采用能量法求解圆锥壳结构的固有频率。朱显明等[12]基于Donnell壳体理论,应用幂级数法求解了圆锥壳的振动特性。陈美霞等[13]采用Donnell壳体理论及幂级数法,对不同边界下截锥壳体的振动特性对比发现,边界约束越多,频率值越大。王宇等[14]采用解析法分析了薄壁圆柱壳不同边界下的高阶振动特性。周云泽等[15]采用Donnell运动方程和幂级数法,计算了两端简支条件下截锥壳的低阶固有频率。洪杰等[16]通过模态试验分析了薄壁壳结构的振动特性,但缺乏理论研究。
本文针对薄壁截锥壳,基于Love壳体理论和传递矩阵法,利用Mathematica编程,在简支-简支、固支-固支和大端固支-小端自由三种边界条件下,求解薄壁截锥壳的高阶振动特性,并通过文献和有限元仿真进行对比验证。
1 基于传递矩阵法薄壁截锥壳的模态特性求解
1.1 结构模型
薄壁截锥壳的模型如图1所示。引入(s,θ,z)坐标系,s代表截锥壳的母线方向,θ代表截锥壳的圆周方向,z代表截锥壳的面法线方向。u,v,w分别表示s,θ,z方向上相对应的振动位移。

图1 薄壁截锥壳模型Fig.1 Thin-walled truncated cone shell model
设薄壁截锥壳母线长为L,厚度为H,壳体大端半径为R2(坐标系原点),半锥角为α,薄壁截锥壳上任一点半径为R=R2-s⋅sinα。将薄壁截锥壳沿长度方向分为N段,各段壳体的子午线长度分别为L1,L2,L3,…,Lk,…,LN(1≤k≤N)。
1.2 模态特性求解
基于Love壳体理论,建立薄壁截锥壳的动力学平衡方程为[17]

式中:Ns,Nθ和Nsθ分别为中面上单位长度的薄膜力和薄膜剪力;Qs,Qθ分别为s和θ方向中面上单位长度的横向剪力,表达式为
式中:Ms,Mθ,Msθ分别为s和θ方向中面上单位长度的弯矩和扭矩。
对于各向同性的薄壁截锥壳,内力与内力矩的表达式为


式中:K为薄膜刚度;D为弯曲刚度;μ为泊松比;E为杨氏模量。

基于Love壳体理论,引入等效Kirchhoff面内剪力P和横向剪力T,计算式为

设模态薄壁截锥壳的动力平衡方程的位移解为

式中:ωmn表示薄壁截锥壳的固有频率;m、n分别表示轴向半波数和周向波数,即节径数。
薄壁截锥壳的中面转角ϑs和ϑθ分别为
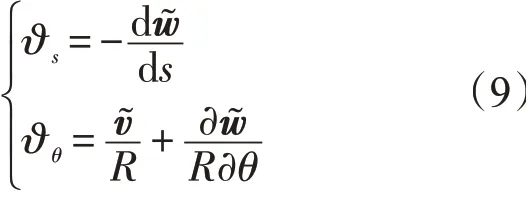
将位移函数式(8)代入式(9),得

将位移函数式(8)代入式(2)、式(3)、式(4)、式(6)和式(7),得

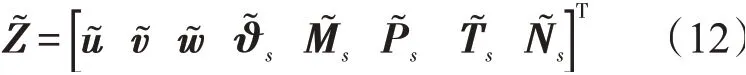


如图1所示的薄壁截锥壳,可以将将壳体分为n0段,有n0+1个分段截面0,1,2,…,n0,从截锥壳的一个端面到另一个端面的传递矩阵关系为
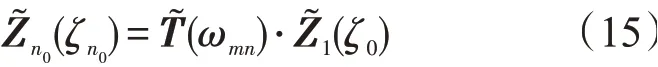
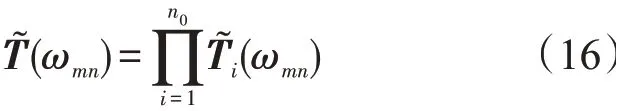
每一段薄壁截锥壳的传递矩阵关系定义

对于第i段薄壁截锥壳

为了精确求解,对于具有同一厚度的每段薄壁截锥壳体,沿轴线方向划分长度为L1,L2,…,Lk的k个子段,其传递矩阵关系式

式中:G͂(Lk)是薄壁截锥壳每一个子段间的传递矩阵

采用传递矩阵法分析薄壁截锥壳体的固有特性时,由于不同边界条件的限制,导致特征方程不同。

当式(21)的系数行列式为零时,可求得薄壁截锥壳的固有频率,即

(2)固支-固支边界条件。对于固支-固支边界条件,u͂=v͂=w͂=ϑ͂s=0,可得整体传递矩阵关系

(3)大端固支-小端自由边界条件。对于大端固支-小端自由边界条件,,可得整体传递矩阵关系

将薄壁截锥壳具体的几何参数和材料参数代入后,利用精细积分法[18]即可得到其固有频率。
2 结果验证与算例分析
2.1 结果验证
首先对本文分析方法的有效性进行验证。薄壁截锥壳的材料参数和几何参数如表1所示。

表1 薄壁截锥壳材料和几何参数Tab.1 Material and geometric parameters of thin-walled truncated conical shell
在简支-简支边界条件下,基于传递矩阵法和有限元法求得薄壁截锥壳的固有频率,具体数值见表2,并与文献[6]中的改进傅里叶级数法进行对比,如图2所示。采用三种方法求得的固有频率变化趋势基本一致。传递矩阵法和有限元方法的计算结果与文献[6]的误差最大0.53%,验证了本文分析方法的正确性。

表2 薄壁截锥壳的固有频率,HzTab.2 Natural frequencies of thin walled truncated conical shell,Hz

图2 两端简支边界下薄壁截锥壳的固有频率Fig.2 Natural frequencies of thin walled truncated conical shells with boundary condition of simply-simply support at both ends
2.2 算例分析
采用Mathematica编程的传递矩阵法和有限元法,分别求解薄壁截锥壳在固支-固支、简支-简支和大端固支-小端自由三种边界条件下的高阶模态振动特性。选取Ti-6Al-4V钛合金[19-20]作为薄壁截锥壳材料,其材料参数和几何参数如表1所示。
2.2.1 固支-固支边界条件 在固支-固支边界条件下,利用传递矩阵法计算薄壁截锥壳的高阶固有频率,并与有限元法计算结果进行比较。周向波数n=1~20,轴向半波数m=1~3时,两种方法得到的固有频率随周向波数的变化曲线如图3所示,薄壁截锥壳部分模态振型如图4所示。

图3 薄壁截锥壳高阶固有频率变化曲线Fig.3 High-order natural frequency change curve of thin-walled truncated conical shell
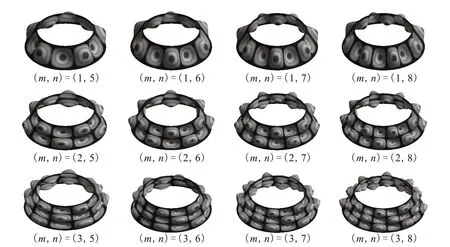
图4 固支-固支边界下薄壁截锥壳的模态振型图Fig.4 Modal diagrams of thin-walled truncated conical shell under boundary condition of clamped-clamped support
利用传递矩阵法和有限元法得到的薄壁截锥壳高阶固有频率变化曲线吻合,相对误差最大为1.56%。周向波数n由低阶到高阶的过程中,固有频率先减小后增大,且阶数越高增幅越大;随着轴向半波数m的增大,固有频率也随之增大。当m=1,n=7时,固有频率最小,为400.1 Hz。当m=1,n=20时,固有频率最大,为2 106 Hz。
由于固支对边界条件的约束,薄壁截锥壳的三维模态振型在低阶时主要以周向模态振动为主,高阶时为周向和轴向模态的组合振型。
2.2.2 简支-简支边界条件 在简支-简支边界条件下,两种方法求得薄壁截锥壳固有频率随周向波数的变化曲线如图5所示,薄壁截锥壳部分模态振型如图6所示。
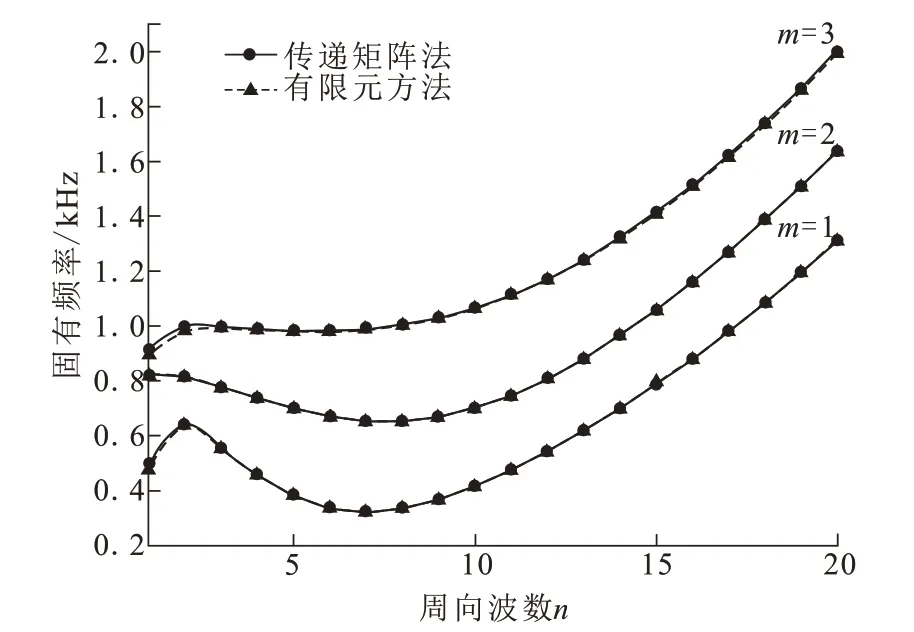
图5 薄壁截锥壳高阶固有频率变化曲线Fig.5 High-order natural frequency change curve of thin-walled truncated conical shell

图6 简支-简支边界下薄壁截锥壳的模态振型Fig.6 Modal diagrams of thin walled truncated conical shell under boundary condition of simply-simply support
利用传递矩阵法和有限元法求得的薄壁截锥壳高阶固有频率曲线变化趋势基本一致,相对误差在5%以内。与固支-固支条件下计算结果不同的是,在n=1时频率下降。在m=1~3,n=2~20范围内,周向波数n由低阶到高阶的过程中,固有频率先减小后增大;最小固有频率出现在m=1,n=7处,为325.6 Hz;随着轴向半波数m的增大,固有频率也随之增大;当m=3,n=20时,固有频率最大,为2 002.3 Hz。
由于两端简支对两侧节点的限制作用,使三维模态振型主要表现为中部的位移。
2.2.3 大端固支-小端自由边界条件 在大端固支-小端自由边界条件下,薄壁截锥壳高阶固有频率随m和n的变化曲线如图7所示,薄壁截锥壳部分模态振型如图8所示。

图7 薄壁截锥壳高阶固有频率变化曲线Fig.7 High-order natural frequency change curve of thin-walled truncated conical shell

图8 大端固支-小端自由边界下薄壁截锥壳的模态振型Fig.8 Modal diagrams of thin walled truncated conical shell under boundary condition of large end clamped-small end free support
利用传递矩阵法和有限元法求得的薄壁截锥壳高阶固有频率曲线重合,相对误差在2%以内。周向波数n由低阶到高阶的过程中,固有频率先减小后增大。同时,当轴向半波数增加时,固有频率明显增大。当m=1,n=6时,固有频率最小,为226.1 Hz;当m=3,n=20时,固有频率最大,为1 913.0 Hz。
大端固支-小端自由边界条件下,三维模态振型低阶时主要以周向模态振动为主,且表现为自由端节点的振动,即自由端的振动位移最大。这是因为固定端约束了各节点的位移。
3 结论
基于Love壳体理论和传递矩阵法求解了三种边界条件薄壁截锥壳的高阶固有频率,并与文献和有限元法计算结果进行对比。
(1)采用传递矩阵法和有限元法计算固有频率值与文献数据基本一致,对比误差最大0.53%。验证了传递矩阵法计算的准确性。
(2)在固支-固支、简支-简支和固支-自由边界条件下,采用传递矩阵法和有限元法计算薄壁截锥壳高阶固有频率相对误差较小,且变化趋势吻合。在固支-固支和大端固支-小端自由边界条件下,高阶固有频率随周向波数的增大先减小后增大,当轴向半波数增加时固有频率明显增大。在简支-简支边界条件下,n=1时呈现出频率下降的现象,而在m=1~3,n=2~20范围内,频率随周向和轴向波数的变化规律与前两者相同。
(3)薄壁截锥壳在固支-固支和简支-简支边界条件下,固有频率在m=1、n=7处取得最小值;在大端固支-小端自由边界条件下,在m=1、n=6处取得最小值。三种边界下最小值频率值分别为400.1、325.6和226.1 Hz。最低阶固有频率随边界条件的不同而变化,边界条件约束越多,频率越大。固支-固支边界条件下,频率随轴向半波数变化的速率较快。
(4)三种边界条件下的模态振型低阶时主要以周向模态振动为主,高阶时出现了周向和轴向叠加的模态振型。
附录1


附录2



