系泊双浮体波能转换装置的水动力性能
纪仁玮, 胡 超, 李乐飞, 夏 淼, 陈甫昕, 张学伟
(1.哈尔滨工程大学 船舶工程学院,哈尔滨 150001;2.江苏科技大学 船舶与海洋工程学院,江苏 镇江 212001;3.国网安徽省电力有限公司 全椒供电公司,安徽 全椒 239500)
0 引 言
随着科学技术的不断进步和经济的飞速发展,以及环境污染问题日益严重和化石燃料日渐枯竭,对可再生、绿色环保能源进行开发和利用成为当今社会最重要的研究课题之一。波浪能作为一种环保、可再生、便于利用且储量丰富的新型能源,逐渐引起人们的重视[1]。波浪能的开采和利用主要通过波浪能发电装置完成,振荡浮子式波浪能发电装置作为当今最具优势的波浪能装置之一,已成为波浪能研究的热点[2-3]。
本文主要研究振荡浮子式系泊双浮体波能转换装置的垂荡运动响应RAO(Response Amplitude Operator)和能量俘获宽度比的变化规律,具体包括:
1) 基于势流理论,利用ANSYS-APDL软件建立单浮体和双浮体模型,并将其导入到AQWA-LINE模块中计算出响应的水动力系数,包括浮子和浮筒的附加质量、辐射阻尼、垂荡波浪力及浮子与浮筒之间相互耦合的附加质量和辐射阻尼;
2) 运用Mathematica编程进行数值迭代,求解单浮体、双浮体波能转换装置的垂荡运动响应和能量俘获宽度比;
3) 通过对上述数据进行处理,详细分析单浮体和双浮体波能转换装置的水动力性能。
1 基本理论
1.1 基本假设
基于频域势流理论,考虑到在开敞水域浮体的尺寸相对较小,在分析过程中作以下假设:
1) 流体不可压缩,忽略黏性,且运动无旋;
2) 在开敞水域,海平面无限大,海底均匀等深;
3) 入射波为线性规则波,满足微幅波假定,且波长远大于波高;
4) 浮子在波浪的作用下作简谐运动。
1.2 频域势流理论的基本方程


(1)
对于不可压缩、无旋的理想流体,速度势满足拉普拉斯方程,即
(2)

根据伯努利方程得到流场中压力P与速度势φ的关系式为
(3)

满足拉普拉斯方程的解有无穷多个,若要得到唯一解,必须补充所研究问题的边界条件和初始条件。
1.3 作用在浮体上的外力
1.3.1 波浪激励力
波浪激励力由弗劳德-克雷洛夫力和绕射力2部分组成,可表示为
(4)
式(4)中:ρ为海水密度;ΦI为入射势;ΦD为绕射势;dS为湿表面;n为广义外法线矢量在垂直方向上的分量。
1.3.2 辐射力
辐射力是物体在理想流体中运动产生的辐射波反过来作用在物体上的力,在垂直方向上,其计算式为
(5)
式(5)中:ΦR为辐射势。
1.3.3 静水恢复力
当物体在液面处作小幅度的简谐运动时,所受重力保持不变,随着吃水的变化受到波浪给予的一个简谐变化的浮力,其大小与物体的形状和物体与自由液面的相对位置有关。静水恢复力的表达式为
(6)
1.3.4 能量输出负载
波能转换装置输出电能的过程是在吸收波浪能并将其转换成机械能之后,通过液压系统将该机械能转换为电能,过程中波能转换装置会受到电力输出系统施加给浮体的能量输出载荷的作用,能量输出负载的计算式可表示为
(7)

1.4 系泊线准静态分析

图1 悬链式系泊线示意
图1为悬链式系泊线示意,为方便计算,设海底表面为水平面,水深为h(即悬链式系泊线最上端端点R到海床底部的垂直距离),系泊线最上端端点R与载体平台相连接,系泊线最底端端点O与海床相切。系泊线受到平台的拉力TR,该拉力可分为水平分力TRx和垂直分力TRy。系泊线的总长为l,系泊线最上端和R点处的切线与水平轴的夹角为θ。在推导过程中,只考虑系泊线自身重力的作用,不考虑其他任何外界载荷的影响。
由受力平衡条件可知:悬链式系泊线的水平受力T0与系泊线末端连接的系泊点R的水平分力TRx大小相等,且在系泊线任意处的水平力均为定值;系泊线的垂直分力TRy等于系泊线在水中的重力(即其湿重)。
(8)
式(8)中:w为悬链式系泊线的单位长度湿重。
由式(8)可得系泊线的一阶导数为
(9)
式(9)两边对x求微分,可得
(10)
(11)
选定坐标原点O,系泊线在x=0处的边值条件为
z(0)=z′(0)=0
(12)
将边值条件代入式(11),可得
(13)
根据式(9)可求得系泊线的长度为
(14)
若将系泊线的长度表示成纵坐标z的函数,可得
(15)
根据式(15)可求得系泊线张力的水平分量与系泊线长度和高度的关系式为
(16)
根据式(8)和式(16)可求得系泊线在各截面上的张力为
(17)
由以上数学表达式可知,在水深z和系泊线单位长度质量w已知的情况下,只需得到悬链线的相关参数T0/w,即可求出悬链线全段的状态参数[5]。
1.5 能量俘获宽度比
俘获宽度比是衡量波能转换装置能量吸收率的重要指标,浮子的俘获宽度比η定义为浮子的平均输出功率与浮子宽度内波浪输入功率之比,可表示为
η=Pa/Pi
(18)
式(18)中:Pa为浮子的平均输出功率,W;Pi为浮子宽度内一个周期内波浪的平均功率,W。
入射波的平均功率Pi可表示为
(19)
式(19)中:H为波高,m;T为波浪周期,s;D为浮子的直径,m。
浮子的平均输出功率Pa可表示为
(20)
式(20)中:FG为电机作用在浮子上的阻尼力,N;v为浮子的垂荡速度,m/s;t2-t1=nT,n为整数。
2 模型建立与计算
2.1 理论模型
本文主要研究的是浮体在垂荡方向上的运动响应,建立单浮体和双浮体的运动模型分别见图2和图3。

图2 单浮体运动模型

图3 双浮体运动模型
2.2 AQWA-LINE水动力分析
在建立简化模型时,为与单浮体进行对比分析,将模型的浮子尺度半径与单浮体的尺寸设置一致。假设双浮体装置自由漂浮在水面上,双浮体的质量在壳体上均匀分布。模拟的环境参数为:海底平坦,水深h=50 m;流体密度ρ=1 025 kg/m3;重力加速度g=9.81 m/s2。通过对悬链线公式进行相关推导,可得到4根锚链的长度均为86.8 m,锚链的单位长度质量为17.5 kg/m,总质量为6 068 kg,4根锚链总的等效刚度Km=14 245.34 N/m。在ANSYS/APDL中建立单浮体和双浮体频域模型(见图4和图5)。
在AQWA-LINE模块的数值模拟计算中,设定分布在0.1~3.0 rad/s区间内的30个单位振幅的线性规则波的频率为入射波频率,计算入射波传播方向与x轴正向的夹角为0°~180°的等角度分布的25个方向的水动力系数,包括浮子和浮筒的附加质量、辐射阻尼、垂荡波浪力及浮子与浮筒之间相互耦合的附加质量和辐射阻尼[7-9]。直接利用得到的水动力参数,在Mathematica中进行编程,求解得到垂荡运动响应和能量俘获宽度比的数据,通过整理数据、制作图表,直观地得到双浮体运动响应和能量俘获宽度比的变化规律[10]。

图4 单浮体频域模型

图5 双浮体频域模型
3 双浮体与单浮体对比分析
3.1 特定阻尼下非线性系数α对能量俘获宽度比的影响
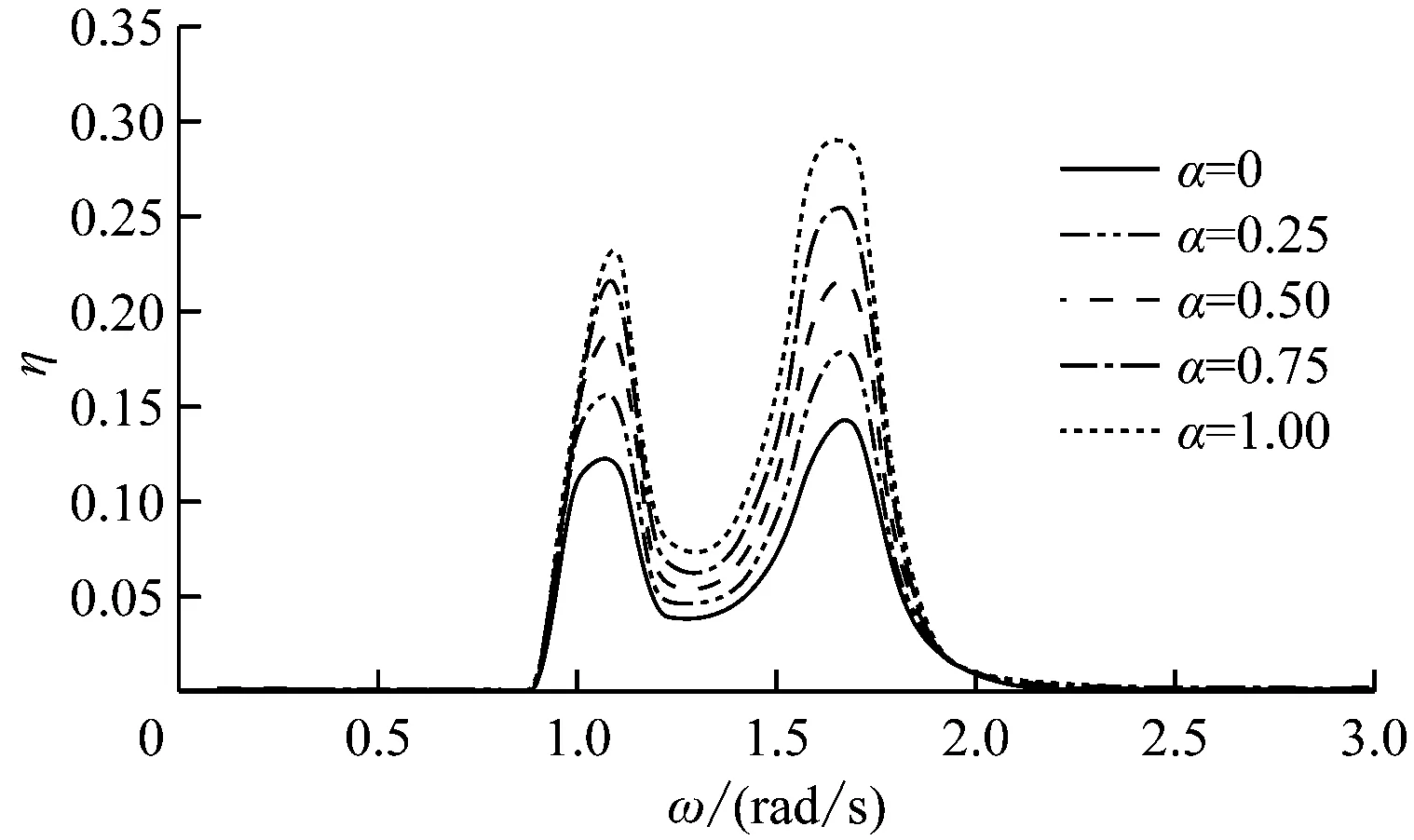
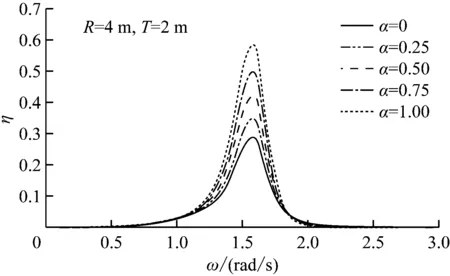
在阻尼系数cPTO为3 000 N·(s/m)α+1、10 000 N·(s/m)α+1和30 000 N·(s/m)α+1等3个特定值的情况下,得到非线性系数α为0、0.25、0.50、0.75和1.00的双浮体和单浮体的俘获宽度比随频率变化的曲线见图6~图8。
a) 双浮体

b) 单浮体

a) 双浮体
b) 单浮体
由图6a、图7a和图8a可知,双浮体在阻尼较小的情况下会出现双峰值,随着阻尼的增大,双峰逐渐消失。如图6所示,当阻尼较小时,尽管转换效率较低,但对非线性较敏感,转换效率会随着非线性的增强而提高,随着阻尼的增大,非线性系数对俘获宽度比的影响越来越不明显。对此,双浮体转换装置在阻尼较小时可通过增强PTO阻尼力的非线性程度来提高波能转换效率;在阻尼较大的情况下,没有必要增强PTO阻尼力的非线性程度。
与单浮体曲线(图6b、图7b和图8b)相比,在小阻尼(cPTO=10 000 N·(s/m)α+1)条件下,当非线性条件一致时,双浮体转换效率曲线下的面积明显比单浮体大。在有效频宽内(如0.9~1.9 rad/s内),双浮体转换效率一直处于较高的水平;对于实际海况下的波浪条件,双浮体的优势更明显。随着阻尼的增大,当非线性程度较弱时,双浮体的这种优势依然存在,不过随着非线性的增强,单浮体转换效率的优势更加明显。

a) 双浮体

b) 单浮体
3.2 特定非线性系数α下阻尼对能量俘获宽度比的影响
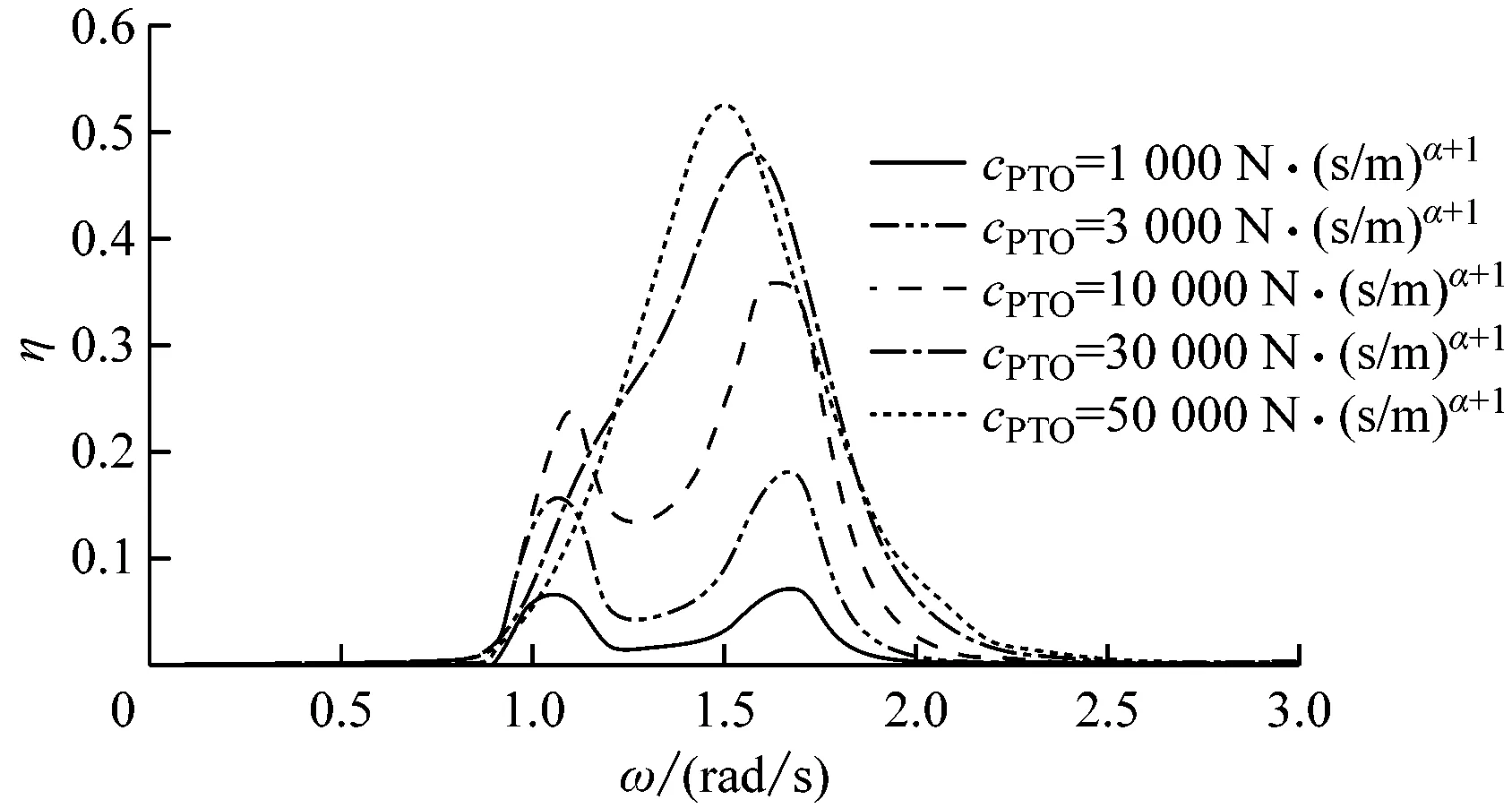
在给定非线性系数α为0.25、0.50和1.00的情况下,得到阻尼系数cPTO为1 000 N·(s/m)α+1、3 000 N·(s/m)α+1、10 000 N·(s/m)α+1、30 000 N·(s/m)α+1和50 000 N·(s/m)α+1时双浮体和单浮体的俘获宽度比随频率变化的曲线见图9~图11。
a) 双浮体

b) 单浮体

a) 双浮体

b) 单浮体

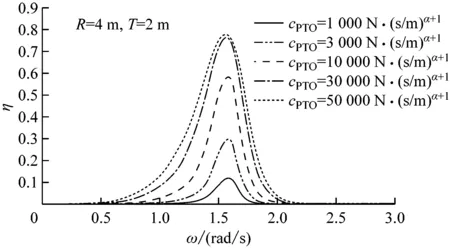
图11 α=1.00情况下双浮体和单浮体的俘获宽度比随频率变化的曲线
由图9~图11可知,在非线性条件一致的情况下,双浮体可通过增大阻尼来提高波能转换效率。当非线性系数不变时,若阻尼较小,如cPTO为1 000 N·(s/m)α+1和3 000 N·(s/m)α+1时,无论是吸收波能频宽还是波能转换效率的总效益S,双浮体的性能均比单浮体好。但是,随着非线性的增强,在阻尼较大的情况下,单浮体的性能明显优于双浮体。因此,随着非线性的增强,双浮体的转换效率始终保持微小改变,而单浮体的俘获宽度比会因非线性的增强而明显增大。
3.3 特定频率下非线性系数α和阻尼对俘获宽度比的影响
选取双浮体的垂荡运动出现明显共振的2个频率ω=1.1 rad/s、ω=1.6 rad/s和非共振频率ω=2.1 rad/s为特定频率,主要探讨非线性系数α和阻尼对双浮体能量俘获宽度比的影响,结果见图12~图14。

a) 双浮体

b) 单浮体

a) 双浮体

b) 单浮体

a) 双浮体
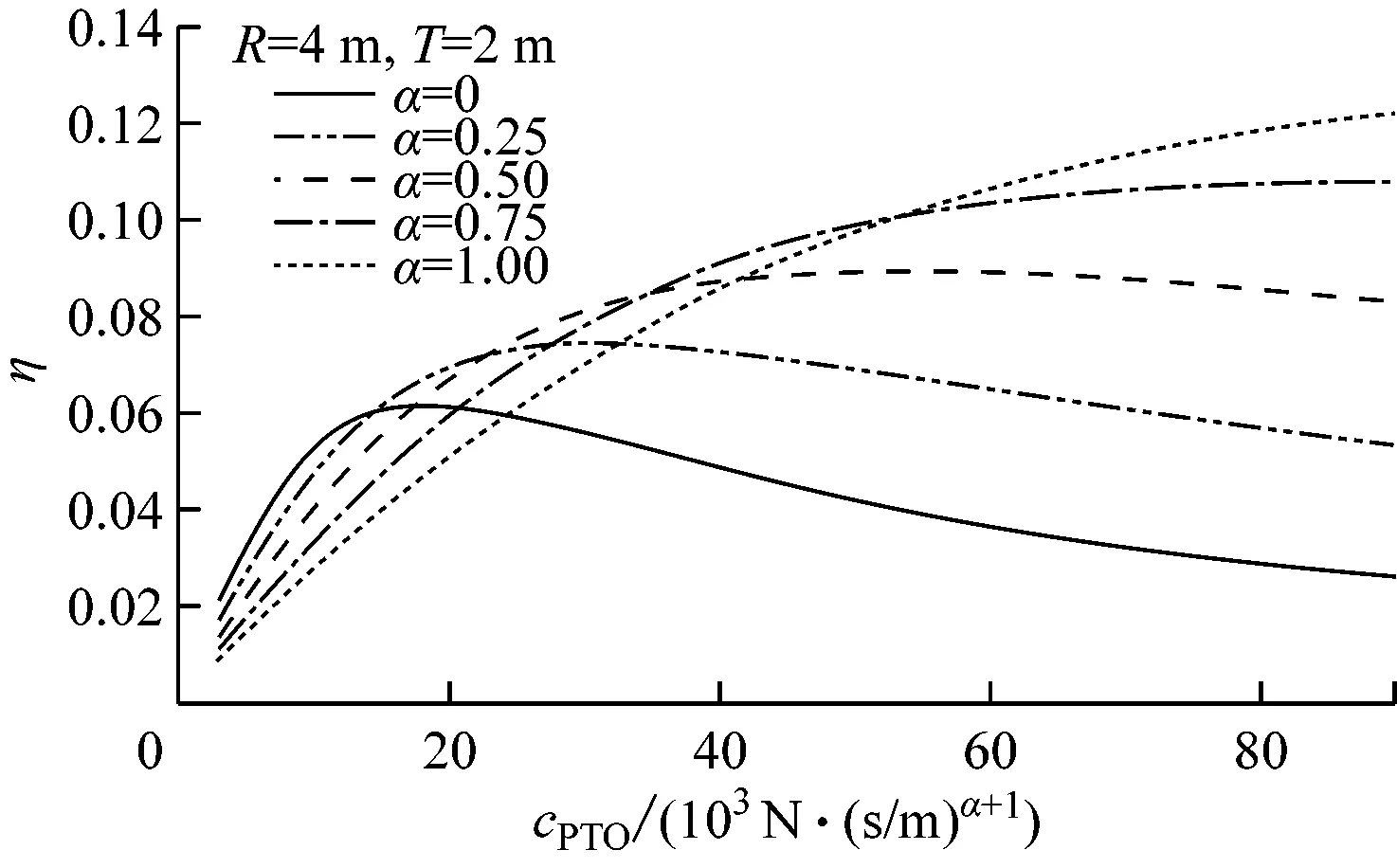
b) 单浮体
由图12~图14可知:在ω=1.1 rad/s情况下,相比于单浮体,双浮体在阻尼较小的情况下即达到峰值,而该范围内的阻尼在单浮体曲线中甚至呈线性增长,且转换效率不如双浮体高,单浮体要达到最佳转换效率,必须通过增大阻尼来弥补,其阻尼数量级达到105,是双浮体的10倍,甚至更大;在ω=1.6 rad/s情况下,双浮体在各非线性条件下的峰值几乎不变,而单浮体的峰值随着非线性的增强而增大,在共振频率范围内,双浮体可通过增强非线性程度来使装置的转换效率在小阻尼情况下就达到最优;在ω=2.1 rad/s情况下,装置的波能转换效率明显不如共振区。因此,应根据波浪能装置的实际情况选择波浪频率与装置固有频率接近的海域,以显著提高波浪能装置的吸收效率。
4 结 语
本文主要通过ANSYS-APDL建立单浮体和双浮体简化模型,在AQWA中计算得到波能转换装置的水动力系数,包括浮子和浮筒的附加质量、辐射阻尼、垂荡波浪力及浮子与浮筒之间相互耦合的附加质量和辐射阻尼。直接利用得到的水动力参数,在Mathematica中进行编程,求解得到波能转换装置的垂荡运动响应和能量俘获宽度比,并对双浮体和单浮体的能量俘获宽度比的变化规律进行对比分析,得到以下结论:
1) 双浮体的波能转换效率并不完全优于单浮体,在某些情况下其性能甚至不如单浮体;
2) 与单浮体相比,双浮体若在较小的PTO阻尼条件下提升非线性系数,其波能转换效率会优于单浮体,吸能频宽也比单浮体大;
3) 随着阻尼的进一步增大,单浮体对非线性的敏感程度不如双浮体,因此在非线性较强时,双浮体的性能优于单浮体,同时双浮体的吸能频宽相比单浮体会增大。

