等比数列实际应用赏析

■江苏省太仓市明德高级中学 王佩其

等比数列实际应用赏析

■江苏省太仓市明德高级中学 王佩其

等差数列无处不在,等比数列也是如此,下面给同学们举上几例。

一、节能减排问题

我国积极应对气候变化,提出到2020年碳排放强度要达到比2005年下降40%的减排目标。已知2005年我国碳排放强度约为3吨/万元,以后每年的碳排放强度均比上一年减少0.08吨/万元。

(1)问能否在2020年实现减排目标,并说明理由。

(2)若2005年我国国内生产总值为a万元,且以后每年均以8%的速度递增,问从哪年起二氧化碳排放量开始减少。注释:“碳排放强度”是指每万元国内生产总值的二氧化碳排放量。

解析:(1)依题意知,自2005年起每年的碳排放强度构成等差数列{an},且a1=3,公差d=-0.08,所以an=3+(n-1)·(-0.08)=3.08-0.08n。因此,2020年碳排放强度为a16=1.8。又3.0×(1-40%)=1.8,所以2020年能实现减排目标。

(2)从2005年起,逐年国内生产总值构成首项为a,公比为1.08的等比数列,所以第n年国内生产总值为a·1.08n-1万元。由(1)知第n年碳排放强度为an=3.08-0.08n,故第n年全国二氧化碳排放总量为bn=a·1.08n-1·(3.08-0.08n)。

所以bn+1=a·1.08n·(3.08-0.08n-0.08)=a·1.08n·(3-0.08n)。

因此,bn+1-bn=a·1.08n·(3-0.08n)-a·1.08n-1·(3.08-0.08n)

=a·1.08n-1·(0.16-0.0064n)。

由bn+1＜bn,解得n≥25。

故从第26年也就是2030年开始,全国二氧化碳排放的总量开始减少。

点评:在实际问题中,常常遇到有关平均增长率(如复利、人口增长率、产值增长率等)的问题,求解时常用到公式y=N(1+p)x,其中N表示原来产值的基础数,p为平均增长率,y表示对应于时间x的产值。

二、中国人口问题

中国人口已经出现老龄化与少子化并存的结构特征,测算显示中国是世界上人口老龄化速度最快的国家之一,再不实施“放开二胎”新政,整个社会将会出现一系列的问题。若某地区2015年人口总数为45万,实施“二胎”新政后专家估计人口总数将发生如下变化:从2016年开始到2025年每年人口比上年增加0.5万人,从2026年开始到2035年每年人数为上一年人数的99%。

(1)求实施新政策后第n年的人口总数an的表达式(注:2016年为第一年);

(2)若新政实施后的2016年到2035年人口平均值超过49万,则需调整政策,否则继续实施,问到2035年后是否需要调整政策。(说明:0.9910=(1-0.01)10≈0.9。)

解析:(1)由题意可知,从2016年开始到2025年每年人口数成等差数列,而从2026年开始到2035年每年人口数组成一个等比数列,由等差数列与等比数列的通项公式写出即可。

当n≤10时,数列{an}是首项为45.5,公差为0.5的等差数列,故an=45.5+0.5×(n-1)。

当n≥11时,数列{an}是公比为0.99的等比数列,又a10=50,所以an=50×0.99n-10。

因此,实施新政策后第n年的人口总数an(单位:万)的表达式为:

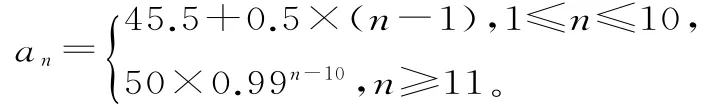
(2)先求出从2016年到2035年的人口总数S20,再求其平均值即可。

设Sn为数列{an}的前n项和,则从2016年到2035年共20年,由等差数列及等比数列求和公式得:

S20=S10+(a11+a12+…+a20)

=477.5+4950×(1-0.9910)≈972.5(万)。

点评:本题难度中等,考查了数列知识的实际应用。本题命题的着眼点是当今社会的热点:“二胎”新政和社会老龄化问题。用数列知识来诠释社会问题,体现出数学与现实的密不可分。

三、我国数学史上的等比数列

《算法统宗》全称《新编直指算法统宗》,是中国古代数学名著,由明代数学家程大位著。书中有这样一个问题:“三百七十八里关,初步健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还。”

题目的大意为:“有一个人走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地。”则该人最后一天走的路程是多少?

解析:仔细阅读题目,不难看出这是个等比数列问题,可以归结为“知三求二”的基本题型。

记每天走的路程里数为{an},则数列的等比数列,且该数列的前六项之和S6=378。

由等比数列前n项求和公式,可得S6=

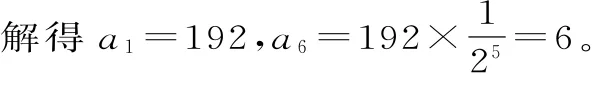
所以该人最后一天走的路程是6里。

(责任编辑 徐利杰)