经典题突破方法

■江苏省太仓市教师发展中心 邵 红

经典题突破方法

■江苏省太仓市教师发展中心 邵 红

我们知道,已知一个数列是等比数列及其首项和公比,求这个数列的通项,是件轻而易举的事。若不知该数列是否为等比数列时,我们如何来求它的通项呢?一个字“变”!真可谓:变一变,天堑变通途。

1.利用递推关系,“变出”等比数列

已知等比数列{an}的首项a1=1,公比0＜q＜1,设数列{bn}的通项为bn=an+1+an+2,求数列{bn}的通项公式。

分析:数列{an}是等比数列,那么{bn}也是等比数列吗?可试探是为是常数。

解:由题意知bn+1=an+2+an+3。又{an}是等比数列,公比为q,故:

点评:对于有些数列试题,虽然题目中没有告诉我们它是等比数列,但是我们不妨大胆猜想,利用递推关系判断它是否为等比数列。

2.利用对数函数,“变出”等比数列

若数列{an}中,若a1=3,且an+1=an2(n是正整数),则数列的通项公式an=____。

分析:将an+1=an2两边取对数,可发现{lgan}是等比数列。

解:因为an+1=an2,所以an＞0(n∈N*)。

两边取对数,得lgan+1=2lgan。

{lgan}是以lga1=lg3为首项,2为公比的等比数列,lgan=(lga1)·2n-1=。

点评:通过构造对数函数达到降次的目的,使原来的递推关系转化为等比数列进行求解,从而使问题顺利获解。

3.通过分解常数,“变出”等比数列

已知数列{an}中,a1=1,an=2an-1+1(n≥2),求{an}的通项公式。

分析:{an}虽然不是等比数列,但{an+m}(m是常数)是等比数列吗?

解:an=2an-1+1(n≥2),即an=2an-1+2-1(n≥2),an+1=2(an-1+1)(n≥2)。

又a1+1=2,故数列{an+1}是首项为2,公比为2的等比数列,an+1=2n,即an=2n-1。

点评:这个题目通过对关系式中1的分解,进行适当组合,可得等比数列{an-1},从而达到解决问题的目的。一般地,形如an+1=pan+q(p≠1,pq≠0)型的递推式均可通过待定系数法对常数q分解:设an+1+k=p(an+k)与原式比较系数可得pk-k=

4.通过分解系数,“变出”等比数列

数列{an}满足a1=2,a2=5,an+2-3an+1+2an=0,求数列{an}的通项公式。

分析:递推式an+2-3an+1+2an=0中含相邻三项,因而考虑每相邻两项的组合,即把中间一项an+1的系数分解成1和2,适当组合,可发现一个等比数列{an-an-1}。

解:由an+2-3an+1+2an=0,得an+2-an+1-2(an+1-an)=0,即an+2-an+1=2(an+1-an)。且a2-a1=5-2=3,故{an+1-an}是以2为公比,3为首项的等比数列,an+1-an=3·2n-1。

利用逐差法可得an+1=(an+1-an)+(an-an-1)+…+(a2-a1)+a1

=3·2n-1+3·2n-2+…+3·20+2

=3·(2n-1+2n-2+…+2+1)+2

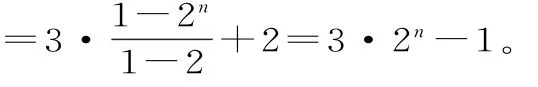
故an=3×2n-1-1

点评:这种方法适用于an+2=pan+1+qan型的递推式,通过对系数p的分解,可得等比数列{an-an-1}:设an+2-kan+1=h(an+1-kan),比较系数得h+k=p,-hk=q,可解得h,k。

(责任编辑 徐利杰)