正、余弦型函数的解题功效

■河南省沈丘县第二高级中学高二(23)班 阮熙杰

正、余弦型函数的解题功效

■河南省沈丘县第二高级中学高二(23)班 阮熙杰

正弦型函数y=Asin(ωx+φ)及余弦型函数y=Acos(ωx+φ),是探究三角函数图像与性质的一个中转站,也就是说我们解答有关三角函数图像与性质的问题,都要先把三角函数化为正弦型函数y=Asin(ωx+φ)或余弦型函数y=Acos(ωx+φ),然后再具体情况具体分析。

一、结合三角函数周期性确定对称轴

点评:正弦型函数的对称轴都经过正弦型函数图像的最高点或最低点,因此,如果是选择题,当我们获取正弦型函数解析式后可以通过检验的方法确定对称轴方程,即把答案中所给的直线方程代入正弦型函数解析式y=Asinωx+φ(),看所得函数值是否为±A。如果所得函数值为A或-A,则可确定该直线方程即为一条对称轴方程。

二、结合三角函数单调性确定参数ω的值

三、结合三角函数奇偶性确定参数值

四、结合三角函数图像平移确定初相

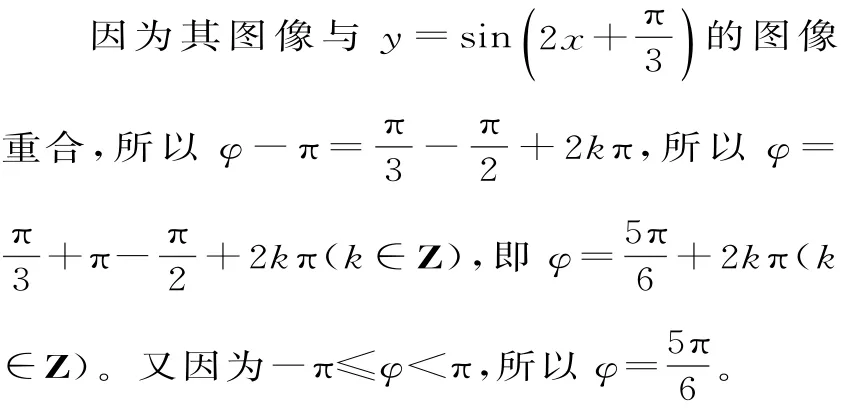
点评:当两个正弦(或余弦)型函数图像重合时,振幅与ω要相同,但是两个初相之间相差2kπ(k∈Z)个单位,即若y=Asin(ωx+φ1)与y=Asin(ωx+φ2)的函数图像重合时,则φ1=φ2+2kπ(k∈Z)。

(责任编辑 赵 平)