数列的求和

■江西省丰城中学 吴爱龙

数列的求和

■江西省丰城中学 吴爱龙

编者的话:基本知识和基本技能是高中数学的核心,同学们一定要高度重视。愿同学们通过阅读,能从中感悟知识的结构与拓展,把握高考命题特点与趋势。

2.已知Sn,求an。

已知数列的前n项和Sn,求数列的通项an时,我们有关系式

3.等差数列的前n项和。

一、考纲要求

掌握等差数列、等比数列的前n项和公式。

二、知识梳理与拓展

1.数列的前n项和。

数列的前n项和通常用Sn表示,其意义是指Sn=a1+a2+…+an。

数列的前n项和是一个专用述语,有其特指的含义。必须理解好三点:①指的是和,而不是n项之积或别的运算。②指的只能是n个项之和,不能多一项或少一项。③指的是前n项之和,而不是某n个项的和,应从第一项开始,一项不少地加至第n项。如果不是从第一项开始,而是从某项开始的连续n项之和,尽管不是数列的前n项和,但也可以借助Sn来表示,比如a3+a4+…+an+2可以表示为Sn+2-S2;也可以用求和符号∑来表

上述第一个公式可由倒序相加法推导。其实它表示上底边长为a1,下底边长为an,高(层数)为n的梯形面积公式;而后两个公式则是将该梯形割或补,变成一个平行四边形的面积na1与一个三角形的面积d之和或变成一个平行四边形的面积nan与一个三角形的面积之差了。特别地,当d=0时,其前n项和Sn=na1。

4.等比数列的前n项和。

已知数列{an}为等比数列,公比为q,则的“ai”是代表项,它代表了a3,a4,…,an+2中的任一项,而∑下方的“i=3”是指求和时从第三项a3开始相加,∑上方的“n+2”指的是最后加至第n+2项an+2终止。这个符号既清晰又简捷,在高等数学中还可以直接参与运算。在初等数学研究方面,常用∑表示循环和,如三角形ABC的三边分别为a、b、c,则其周长可以表示为∑a,即∑a=a+b+c。

如果数列从第一项开始一项不少地加下去,直至无穷,这个和被称作是无穷数列的所有项和,常记为S;任何数列都存在着前n项和,却未必有所有项之和了。当等比数列的公比q满足|q|＜1且q≠0时,其所有项之

常数列既是等差数列,又是等比数列,不论从等差或等比角度看都有Sn=na1。

上述公式可由错位相减法推导,也可以用下面几种方法推得。

方法1:Sn=a1+q(a1+a1q+…+aqn-2)=a1+qSn-1=a1+q(Sn-an)=a1+q(Sn-a1qn-1),n≥2,q≠1。所以Sn=时,亦符合。

方法2:设等比数列{an}的公比q≠1,则

由合比定理有:5.等差(比)数列前n项和的主要性质。

(2)等差数列中,当a1＞0,d＜0时,若ak＞0,ak+1＜0,则Sk最大;当a1＜0,d＞0时,若ak＜0,ak+1＞0,则Sk最小。

(3)等差(比)数列中,非零数列Sk,S2k-Sk,S3k-S2k,…仍成等差(比)数列。

6.数列求和的几种常见方法。

数列求和的常用方法有:倒序相加法、错位相减法、裂项相消法、公式法、分组求和法、奇偶数讨论法等。

三、典例解析与点评

点评:对此解法应注意两点:(1)等差数列前n项和Sn是关于n的没有常数项的二次函数,因此若设Sn=k(7n+2),Tn=k(n+3),则是不合理的;(2)已知数列的前n项和Sn,求数列的通项an时,有关系式an=

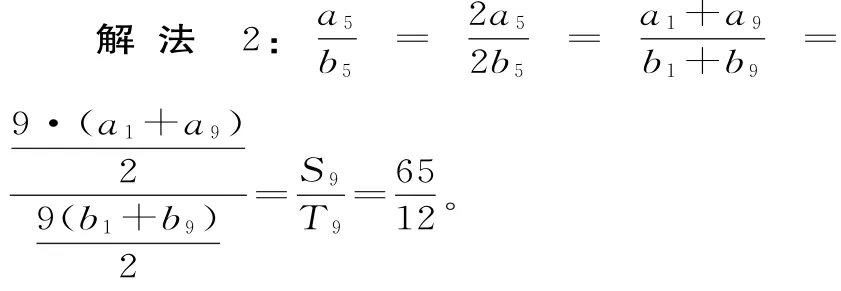
点评:对此解法也应注意两点:(1)等差数列的性质的灵活运用;(2)等差数列求和公式的逆用。

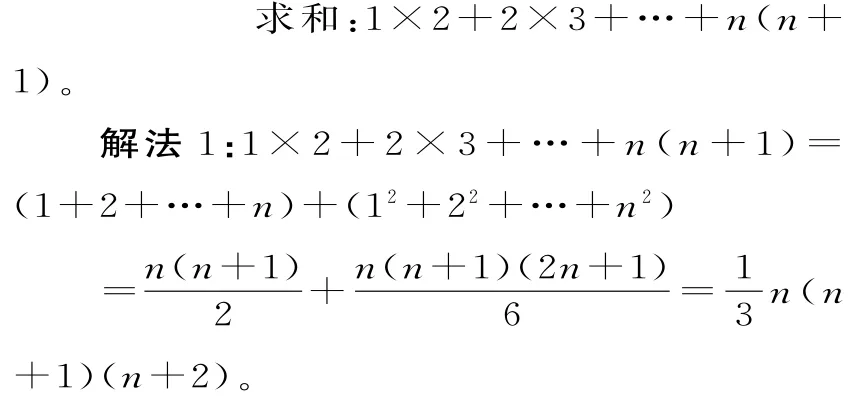
点评:此法是分组求和与公式法求和的完美组合。常用的几个公式

点评:上述方法用的是裂项相消法,裂项(拆项)相消法是数列求和的常用方法之一。裂项是手段,相消是目的。因此,寻找合理的裂项方式是关键。例如一项裂成了两项,但由于无法相互抵消其中的项,所以这种裂项是失败的。对几种常见的裂项应熟记。此外,相消时规律性很强,既然是成对地“裂”,又是成双地“消”,所以必定是成套地“留”。

解法3:学了组合,也可用组合数性质来解。因为n(n+1)=2C2n+1,又Cmn+1=Cmn+Cm-1n,所以1×2+2×3+…+n(n+1)=(n+2)。

点评:此解法将数列求和问题转化为组合数求和并利用组合数性质的问题来解,可谓匠心独运。

一般地,我们有1·2·3·…·k+2·3·4·…·(k+1)+…+n(n+1)(n+2)…(n+k)(n,k∈N*,k≥2)。求和S=1+2x+3x2+…+nxn-1。

当x≠0且x≠1时,有:

S=1+2x+3x2+…+nxn-1。

xS=x+2x2+…+(n-1)xn-1+nxn。

点评:上述解法是分类讨论思想与化归思想的完美组合,解题时极易漏掉x=0与x=1时情形的讨论。错位相减法,“错位”是手段,“相减”是目的;如果错位后不能相减,错位就是无功之举;如果错位相减后能将各项系数归一,则错位就是一种漂亮的形式,因为采用错动位置的书写方法是为了将字母x的指数对齐,对整齐后再减才会少出错误。话虽如此,但很多同学具体运用此法时仍会出错,很难对上正确答案,因此我们平时应多加训练。网络上流行一种死记结论的待定系数法,但笔者不推荐使用这种方法。

点评:这里对已知等式两边求导,体现了整体处理思想,当然也可以对所求和式通过求积分的办法求得。有时可能需要多次求导或求积分。

(责任编辑 徐利杰)