相关点法在求轨迹方程中的应用——由教材中的一道例题说起

☉南京师范大学附属中学江宁分校 高铭秀

相关点法在求轨迹方程中的应用
——由教材中的一道例题说起

☉南京师范大学附属中学江宁分校 高铭秀

教材是教师教学、学生学习的主要载体，由于教材容量的有限，不可能将重要题型、主要方法都面面俱到，因此需要我们深入研究、透彻理解、拓展引申教材内容，也包括对教材中例题或习题的探究.下面以一道例题为例说明.

图1

例1 如图1，在圆x2+y2=4上任取一点P，过点P作x轴的垂线段PD，当点P在圆上运动时，线段PD的中点M的轨迹是什么？为什么？

本例的给出为我们求轨迹方程提供了一种重要的方法——代入法，也称相关点法.

点M的轨迹由点P的轨迹决定，而点P在圆x2+y2=4上运动，故可分别设出点M、P的坐标，将点M的坐标用点P的坐标表示，代入已知圆的方程即可知点M的轨迹方程为椭圆.

下面就相关点法在求轨迹方程时的应用，简举几例.

一、以椭圆为背景

（1）求点P的轨迹方程；

解 析 ：（ 1）设P（x，y），M（x0，y0），则

因为点M（x0，y0）在C上，所以，因此点P的轨迹方程为x2+y2=2.

（2）略.

评注：本题与例1根出同源，可以视为例1的逆向变换，求解中利用相关点法，结合已知条件将所求点P的坐标用已知点M的坐标表示，再代入椭圆方程即可求解.

二、以圆为背景

例3 在平面直角坐标系xOy中，以点A（2，0），曲线y=上的动点B，第一象限内的点C，构成等腰Rt△ABC，且∠A=90°，则线段|OC|的最大值是________.

图2

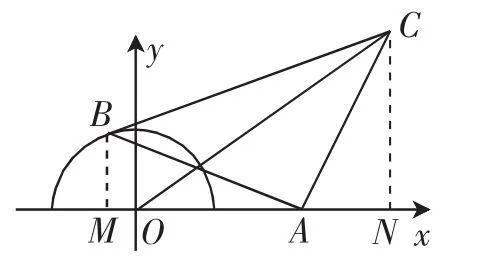
图3

如图3所示，过点B作BM⊥x轴于点M，过点C作CN⊥x轴于点N.易知Rt△BAM≌Rt△ACN，所以BM=AN，MA=CN.

设C（x，y），则B（2-y，x-2）.而点B在圆x2+y2=1（y≥0）上，所以（2-y）2+（x-2）2=1，即点C在以（2，2）为圆心，1为半径的圆上.

评注：本题求解中利用平面几何性质，准确找到点C与B坐标之间的关系，从而利用相关点法求得点C的轨迹方程.

另外也可利用三角换元法解答本题：

设B（cosθ，sinθ）（0≤θ≤π），C（m，n）（m，n＞0）.因为AB⊥AC，则

由①②解得m=2+sinθ，n=2-cosθ或m=2-sinθ，n=cosθ-2（舍去）.

三、以抛物线为背景

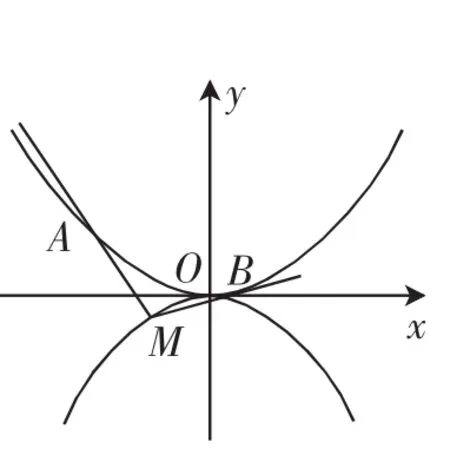
图4

例4 如图4，抛物线C1：x2=4y；C2：x2=-2py（p＞0），点M（x0，y0）在抛物线C2上，过M作C1的切线，切点为A、B（M为原点O时，A、B重合于O），当时 ，切线MA的斜率为

（1）求p的值；

（2）当M在C2上运动时，求线段AB的中点N的轨迹方程（A、B重合于O时，中点为O）.

解析：（1）p=2.（过程略）

联立③④得MA、MB的交点M（x0，y0）的坐标为x0=.根据条件又有M（x0，y0）在C2上，即所以

当x1=x2时，A、B重合于O，AB的中点N为O，坐标满足

评注：本题是典型的求解线段中点的动点轨迹方程的问题.这类题目的特点是需要联立多个方程，计算量比较大且每个方程之间环环相扣，要求书写认真、运算准确.

四、以双曲线为背景

例5 已知双曲线x2-y2=2的左、右焦点分别为F1、F2，过点F2的动直线与双曲线相交于A、B两点.

（2）略.

解析：由条件知F1（-2，0），F2（2，0）.设A（x1，y1），B（x2，y2），M（x，y），则

将式①代入②化简得（x-6）2-y2=4.

当AB与x轴垂直时，x1=x2=2，求得M（8，0），也满足上述方程.

所以点M的轨迹方程为（x-6）2-y2=4.

（2）略.

评注：本题以双曲线为背景，在利用相关点法求解中，也利用了点差法，同时要注意对AB的斜率不存在的情况进行讨论.

综上，求曲线轨迹方程的方法除相关点法以外，还有直接法、定义法、待定系数法等.高三一轮复习在回归课本、夯实基础的同时要注重知识结构、网络体系的形成，以便提高复习的有效性和高考的针对性，这样就真的达到了“做一题，会一类”的效果.F