多层次，宽视野，思讲评——试卷讲评的一些思考

☉江苏省如皋市第二中学 何 敏

多层次，宽视野，思讲评
——试卷讲评的一些思考

☉江苏省如皋市第二中学 何 敏

测试是检验学生知识掌握程度的必备手段，测试后对学生反映的问题如何分析、讲评是后续教学的关键.笔者认为，试卷的命题体现了一定的全面性，对此后续分析学生出现的问题、发现教学的不足、改进后续教学的策略有着重大的关系.笔者多次听试卷讲评的常态课，发现了以下一些问题：

（1）讲评的时效性：试卷的分析和讲评必须是及时的，因为只有及时的分析讲评才能让学生回忆起问题解决过程中出现的那些错误，否则讲评的效果会大打折扣.

（2）讲评的针对性：一堂讲评课的教学时间是有限的，如何在有限的时间里做到讲评的高效率，这必须是有针对性的讲评，特别是对没有思考的讲评，往往是不择重点难点，没有思考拓展，导致讲评课效率低下.

（3）讲评的参与性：讲评要吸收学生的活动，教师一味的讲评是没有实际价值的，因为这种“独角戏”的讲评是教师的思维，而没有学生参与的，我们的试卷讲评主要是给学生以启发，因为学生的参与结合教师的讲评才是最有价值的.

（4）讲评的思维性：不难发现，不少教师的讲评是就题论题的，这种讲评只能说是合格的讲评，还远远谈不上有什么更深的意义.从一些名师的讲评课中，笔者发现其对于试卷的讲评往往是自我分割、有机整合的，即更多是在问题讲评的过程中渗透了命题的意图、运用的思想以及思维的深刻性，这才是笔者最想听的试卷讲评.

一、追求基础，掌握技能

问题1 判断下列函数的奇偶性：

（1）f（x）=2x2+1，x∈［-2，2）；

（2）f（x）=2x2+1，x∈（0，+∞）；

（3）f（x）=|x-2|-|x+2|；

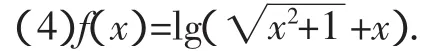
分析：本题是测试中的基本问题，对于函数奇偶性的判断有着基本的方法.学生理解奇偶性判断的方式主要是依据表达式f（-x）=f（x）以及f（-x）=-f（x），对于其他的注意点，相对来说并不是非常关注.要重视奇偶性判断的第一要素是定义域是否关于原点对称，第二要素才是对表达式f（-x）=f（x）以及f（-x）=-f（x）的判断，而且还要注重奇函数中f（-x）=-f（x）表达式的变形使用，针对不同函数模型使用的便捷性.

层次：奇偶性判断要注重层次性教学，笔者建议在讲评完试卷基本问题之后，进行多层次的技能回顾：

层次（1）：①f（x）=2x2+1，x∈R；②f（x）=2x3+x，x∈［-2，2］.

说明：从概念角度回顾奇偶性判断，思考定义域为首要原则，然后进行判断.

说明：对于函数较为复杂的模型，首先要进一步分析定义域，上述两个问题是学生常犯的错误，这两个问题是在基础问题上的一个提升.

层次（3）：①f（x）=g（4+x）+g（4-x）（x∈R）；②g（x）=

说明：讲评的最后，笔者设计了抽象函数和分段函数，相对学生来说，这是奇偶性判断的难点.在这里抽象函数判断的时候，整体思想的使用成为关键；对于分段函数的判断，教学中建议学生多使用奇函数判断表达式的变形即可.①它具有对称性，因为f（-x）=g（4-x）+g（4+x）=f（x），所以f（x）是偶函数，不是奇函数.②当x＞0时，

综上可知，在（-∞，0）∪（0，+∞），g（x）是奇函数.

二、加强变式，发散理解

分析：本题是三角函数求解值域的基本问题，但是有不少学生对于三角值域的求解模型并不清晰，因此在讲评完基本问题后，给出相关的三角函数值域求解变式，加深三角值域问题求解模型的全认识.将原式变形为由知，所以原函数值域为［-2，1］.

变式3：函数 y=（sinx+1）（cosx+1）的值域为___________.

分析：变式1强调的是函数本质的研究，以三角函数为载体的二次函数本质研究是关键.变式2主要考查的是三角公式的运用化简，最终本质依旧是问题2.变式3和变式4依旧以三角函数为载体考查函数的值域，可以站在系统的高度上认识两个函数的模型特征.变式3，本式不是齐次式，显然sinx+cosx是一次的，而sinx·cosx是二次的，因而本题主要是二次函数的最值的思考，变式4如出一辙，可以理解为函数模型，从而形成突破.可以这么说，试题的变式是中学数学的优良传统，是教学有效性的实施手段，因为变式教学可以将知识运用的广度变得灵活，从而学生掌握的知识使用也能灵活多变，这是讲评教学中变式手段使用的因素.

三、一题多解，优化思维

讲评教学中需要关注学生的思维，这种关注思维的体现恰恰是重视学生参与度的表象.在试题讲评分析中，我们经常发现学生并不是与教师在同一个思维来看待问题的.笔者认为，讲评教学应该把这种多思维、多视角的东西带给学生，以便学生获得思维的优化，这才是讲评有效性的体现.将学生合理的思维抹杀，跳过学生思维的讲评方式，都是低效和不负责任的.

问题3已知（fu）=u2+au+（b-2），其中R，x≠0），若a，b可使方程f（u）=0至少有一个实数根，则a2+b2的最小值是__________.

分析：本题是测试中的压轴填空小题，但是参考答案提供的方式并不为学生所接受.原因很简单，参考答案中，由u2+au+（b-2）=0，得至少有一根的绝对值大于2”这一步学生纷纷表示不可能这么处理，因为这样的方程通过求根解决是大忌，显然是不被认可的.学生提出了自己的一些想法，但是又没有办法完全解决，教师的讲评在此时要关注学生的思维，进行合理的点评和分析，寻求思维的优化.

思维1（代数解法）：学生甲认为将u2+au+（b-2）=0进行参变分离，就可以获得更好的思维，但是苦于考试时间有限，未能解决完毕，不妨一起来看看：

利用线性规划知，（*）表示的线性区域如下图所示：图中灰色区域表示a、b的满足的范围，由几何意义知表示点（a，b）到原点距离的平方.从图像观察，原点到线性区域上的点（a，b），是点到直线2a+b+2=0或者2a-b-2=0的距离的平方最短.易由解析几何知识可知，分别在点时取等号.

说明：通过调查发现，学生最普遍的思维是图形的解法，但是学生没有能够好好地解决将一系列不等式所表示的区域转化为图形，从而限制了其进一步的研究.从上述不等式组的约束条件来看，有点类似线性规划的味道，笔者将其称之为“曲线规划”，这种带有非线性约束条件的不等式的处理，往往是学生比较欠缺的，因此讲评的时候切勿以参考答案为主进行，更要从学生的视角进行分析，提升问题解决的普适性.

总之，试卷的讲评还是要多准备一些课前的工作，教师准备得充分，学生在试卷讲评中收获也能越多，不至于学生总是在这样的课堂中无所事事，效率低下.多层次、宽视野、思讲评，是试卷讲评分析工作的一些思考，这些思考有助于教师更好地理解试卷讲评课如何演绎，这是试卷讲评教学的关键.

1.方明.陶行知教育名篇［M］.教育科学出版社，2005.

2.姜兴荣.探求解题思路的几种有效策略［J］.中小学数学，2013（7-8）.

3.宋卫东.从生“动”到生动，诠释思维品质的提升［J］.中学数学月刊，2013（5）.

4.柴贤亭.数学教学中的函数问题设计［J］.教学与管理，2012（10）.