高三二轮复习教学的有效性

☉江苏省南通市通州区金沙中学 季宏玲

高三二轮复习教学的有效性

☉江苏省南通市通州区金沙中学 季宏玲

高三数学复习一般都分为三轮，第一轮复习注重学生对基础知识的回顾和对基本能力的温习，以夯实基础为目标.第二轮复习大概要持续三个月左右的时间，除要根据每年《考试说明》中出现的变化对复习的内容进行调整和加强之外，其余的很多时间还是要进行专题复习和试卷讲评的.怎样才能让学生对第二轮复习保持着高昂的学习情绪和学习兴趣，这就需要教师将二轮复习课上的有深度、有新意，来得更为有效？激发学生内在的学习动力和兴趣，实现课堂的互动，真正实现课堂中以学生为主体.而不能只是按照知识点或者是题型“串讲式”、“满堂灌式”地上复习课和试卷评析课，这种“炒冷饭”式的复习方式会让学生觉得索然无味，时间长了会造成厌烦情绪，失去学习的兴趣和动力.

让课堂有深度、有新意，让学生有兴趣、有动力，并积极参与到课堂活动中来.教师要从不同的层面和角度研究题目、题型、知识和技能，让学生既能强化已知，又能体验到更有深度和价值的新的知识能力.

一、集体探讨，深度分析

复习教学总是教师讲评分析的方式已经落后于当下复习教学的主流，我们更多的是需要引导学生如何去发现复习教学中出现的问题，要让学生从知识层面、心理层面、技能层面、思想层面获得进步，因此集体探讨结合深度分析必不可少，对于问题的选择只需是有针对性的即可，不在于多，更在于精.

问题1：关于x的不等式ax2-|x+1|+2a≥0在R上恒成立，则a的取值范围是_______.

学生给出了以下几种方法：

方 法 1：（直 接 法） 令 f（x）=ax2-|x+1|+2a=然后分类讨论，并画出该分段函数的基本图像，观察图像找出满足条件的不等关系，计算得到结果.

学生评价：分段函数的图像不太容易画，特别是在有参数的情况下，很容易弄错的.而且必须在分类讨论的前提下才能画出草图，太难！

方法2：（变量分离法）将ax2-|x+1|+2a≥0在R上恒成立转化为在R上恒成立，令解得g（x）max=，所以

学生评价：比直接法好一些，因为是具体函数，不带参数字母的.但是分段函数求最值还是有点麻烦.特别是变形成可以使用基本不等式来求最值，这个步骤比较难想到.如果用导数求g（x）的最值，对于一个填空题来说运算量也有点大.

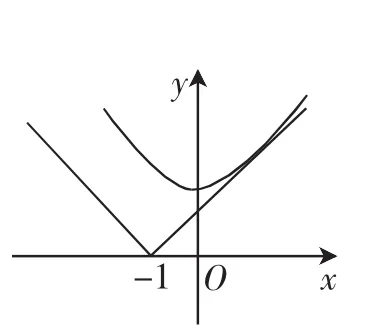
图1

方法3：（图像法）将ax2-|x+1|+2a≥0移项整理得a（x2+2）≥|x+1|，再令n（x）=a（x2+2），m（x）=|x+1|，由题意，n（x）的图像恒在m（x）的图像的上方（如图1），所以首先可以得到a＞0，计算n（x）的图像和m（x）的图像相切的时候的a值为，根据图像的变化即可判定a的取值范围.学生评价：与前两种方法比较运算量最小，图像都是平时很熟悉的二次函数和绝对值函数，位置关系也比较清晰，这个方法最适合这个题目.

共同回顾总结：①知识层面：不等式问题总是和函数、方程是密不可分的，这三个知识点并不孤立，而是一个共同体.②技能层面：在研究不等式恒成立问题时，“变量分离、令函数、求最值”通常是个不错的选择，还可以考虑使用直接法和图像法，比较后选择最优方案.③数学思想层面：“数形结合”是高中阶段非常重要的数学思想之一，充分利用它能将许多问题简化.

二、耐心倾听，深度发掘

学生错误的典型原因、存在的典型困惑，教师应该在课堂教学中给以引导，让学生说出这些困惑和错误.学生的认知水平是比较相近的，学生对一个问题的认识和教师对该问题的认识不是同一个认知水平.学生会从很多不同的角度来分析问题.教师要去倾听，去了解学生的想法，才能有目的地引导学生.不仅能解决阐述问题的学生的困惑，也能促进其他学生的发展.

问题2：某人测量一座山的高度，他在山底所在的水平面上，选取同一直线上的三个点A，B，C进行测量.他在A点测得山顶的仰角为45°，在B点测得山顶的仰角为60°，在C点测得山顶的仰角为30°，若AB=BC=a，则这座山的高度为________（结果用a表示）.答案

学生做题情况：全班只对了一半，没有对的学生中还有7个是空白.首先让空白的部分学生先阐述想法.

学生阐述：“在草稿纸上怎么画都画不出图来”、“我也画不出图，怀疑是不是题目错了”、“我画了个图，可是算了一下AB和BC不可能相等”.

于是让最后发言的那位同学上黑板把他所绘制的图像给大家看（如图2）.并说明：“设山高为x，那么AB=，而，不相等啊，交换一下A，B，C的位置也不相等”.

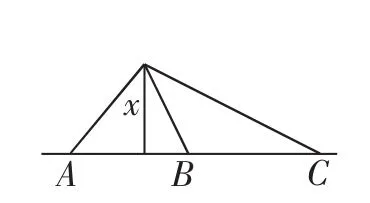
图2

图3

学生更正：这个图像应该是个三棱锥（如图3）.

其次让做错的学生来阐述想法.

学生阐述：“我画的图也是三棱锥啊，可怎么算出来和不对呢？”

于是让学生把条件标在图上，结果把仰角的位置标错了.原来有部分学生并不清楚仰角、俯角的概念.

学生更正：仰角、俯角是视线和水平线的夹角.

通过这样对发生错误的过程的阐述和交流，更正错误、明晰概念，对做对的学生也是一个提醒.也可以让他们在更正其他同学的错误的同时，对自己也是一个提醒.并配上巩固练习强化已知.

练习1：在海岛A上有一座海拔1km的山，山顶上有一个观测点P，下午15：00，测得一所货轮在岛的北偏东30°，俯角30°的B处，15：10又测得该货轮在岛的北偏西60°，俯角60°的C处，则货轮的航行速度为_______.答案：

有些问题穿着美丽的外衣，让你看不清辨不明.遇到这样的问题首先要头脑冷静，仔细审题，思考题目中的那些描述和我们已知的有什么关系，能否转换到熟悉的背景下来.特别是排列组合这一块的内容.

三、转换背景，揭示本质

问题3：为了庆祝六一儿童节，某食品厂制作了3种不同的精美卡片，每袋食品随机装入了一张卡片，集齐三种卡片可获奖，现购买该食品5袋，能获奖的概率为___________.

背景转换：5个不同的小球放到3个不同的盒子中.（1）有多少种不同的放法？（2）若每个盒子至少放一个小球，又有多少种不同的放法？

学生求解：（1）有35种；（2）

相较于本题轻松解决背景转化后的问题，因为这样描述的题目是他们熟悉的环境和背景，学生觉得亲切，又思路清晰.

问题4： 有一类四位数abcd，满足：①a，b，c，d∈｛1，2，3，4｝，②a≠b，b≠c，c≠d，d≠a，③a，b，c，d中至少有两个数字相同，④a是a，b，c，d中最小的，则这样的四位数共有_______个.答案：22.

本题作为测试的填空压轴题，确实难倒了不少学生.一是题目给出的限制条件比较多，学生有点无从下手；二是对条件④的理解有误，认为其他b，c，d只能比a大而不能与a相等.

学生分析：由条件①a，b，c，d∈｛1，2，3，4｝，可以得出a，b，c，d是可能取相同元素的，这个也可以通过条件③印证；由条件②可以得出相邻数不相等，且首尾也不相等；由条件④可知b，c，d只能比a大或与a相等.在这样的分析下学生采用分类讨论的方式来解题：（1）若仅a=c或仅b=d：C24A22*2=8*2=16；（2）若a=c且b=d：

其次，让学生进行背景转换，给问题4寻找一个新的背景，但题目的意思和答案都不变.

图4

学生寻找：有四种深浅不同的颜色，现要对图4中A、B、C、D四块区域进行涂色，相邻区域不同色，A、B、C、D四块区域中至少有两块同色，其中A区域的颜色是A、B、C、D四块区域中最浅的，则不同的涂色方法有_____种.答案：22.

回归到“涂色问题”，背景熟悉方法清晰.

高三数学第二轮复习之感想：高三数学第二轮复习是整个三轮高考复习中最精华的部分.教师要创造一个有深度和新意的学习环境，吸引学生积极地参与到课堂活动中来，让学生在复习课中依然是主体.只有学生主动地、积极地参与才是学生能力提升的真正内在动力，让复习教学来得更为有效.

1.展国培.有效教学，从关注学生开始［J］.中小学数学（高中），2013（1）.

2.渠东剑.探究方法比探究结果更重要［J］.中学数学教学参考（上），2013（4）.

3.石志群.高考数学命题思路分析及复习策略［J］.中学数学月刊，2009（11）.F