“依形定数”谈函数问题的解答

☉江苏省宜兴市第二高级中学 吴勇珍

“依形定数”谈函数问题的解答

☉江苏省宜兴市第二高级中学 吴勇珍

图像是函数的主要表示形式，图像能直观展现出函数的相关性质，如单调性、对称性、定点、零点等.在解答函数有关问题时，借助其图像“依形定数”，往往能顺利找到问题的突破口，实现对问题的简洁求解.下面举例加以说明.

引例（2017年山东卷）已知当x∈［0，1］时，函数f（x）=（mx-1）2的图像与的图像有且只有一个交点，则正实数m的取值范围是（ ）.

解析：函数f（x）=（mx-1）2的图像为抛物线，开口向上，对称轴为顶点坐标为，与y轴的交点为（0，1）.

图1

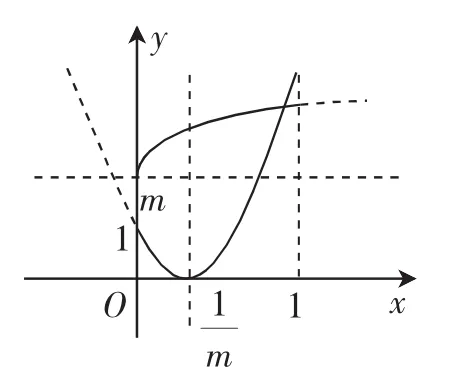
图2

综上所述，m的取值范围为（0，1］∪［3，+∞）.故选B.

评析：本题求解的关键是准确作出两函数的图像，由形确定数的范围.作图时要注意挖掘函数的确定信息，如函数f（x）=（mx-1）2的图像对称轴、顶点坐标以及在y轴上的截距，函数可由的图像向上平移m个单位得到.根据这些信息可确定分类讨论的标准，从而快速确定参数的取值范围.

一、准确寻找临界状态

图3

解析：作出函数f（x）的图像（如图3）.方程f（x）=a（x+1）有三个不相等的实数根，即直线y=a（x+1）与函数f（x）的图像有三个不同的交点.

又直线y=a（x+1）过定点（-1，0），由图3易知，当直线y=a（x+1）与曲线相切时，有两个交点.设此时直线y=a（x+1）的斜率为k，即a=k.所以当0＜a＜k时，两函数有三个不同交点，即已知方程有三个不同实根.因此只要求出k值，问题即可得解.

评析：导数的几何意义：可导函数f（x）在某一点x=x0的导数值f′（x0），即为函数f（x）在点（x0，f（x0））处的切线的斜率.本题中参数范围的确定，关键是找到直线y=a（x+1）与曲线相切时的临界状态，进而利用利用导数的几何意义，求曲线的切线斜率.

二、巧借函数的对称性

A.（0，1）B.（1，4）

C.（0，1）∪（1，+∞）D.（0，1）∪（1，4）

解析：由函数f（x）的图像上有且只有两个点关于y轴对称，则y=logax与y=|x+3|关于y轴对称的图像仅有一个交点.函数y=|x+3|关于y轴对称的函数为y=|3-x|，0＜x≤4.

当0＜a＜1时，如图4所示，符合题意.

图4

图5

当a＞1时，如图5，欲满足题意，须loga4＞1，所以a＜4，即1＜a＜4.

故正确选项为D.

评析：两个函数关于y轴对称，只需要将已知函数中的x换为-x，y不变，即可得到.本题条件中函数f（x）的图像上有且只有两个点关于y轴对称，则将y轴一侧的函数图像沿y轴对称后，与另一侧的函数图像只有一个交点，使问题简洁获解.

三、把握函数的几何意义

解析：由条件中所给关系式的特征，结合直线的斜率公式，假设，则问题等价转化为直线y=kx与函数f（x）的图像交点个数问题.

图6

在平面直角坐标系内作出函数f（x）的图像如图6所示，由图易知，直线y=kx与函数f（x）的图像最多有3个交点，故n的最大值为3.

当n=2时，由图易知，当直线y=kx与曲线g（x）=-x2+4x-3（1≤x≤3）相切时，k取得最大值.

设切点坐标为（x0，y0），对g（x）求导得g′（x）=-2x+4，所以k=g′（x0）=-2x0+4，则有，解得，所以k的最大值为

评析：过点A（x1，y1），B（x2，y2）（x1≠x2）的直线斜率k=，其中可视为过原点的某一直线的斜率，与此类型相关的函数问题，常可借助直线的斜率求解.本题中将条件等价转化为过原点的直线与函数图像交点个数问题，从而将问题直观、简洁求解.

四、明确函数的变化关系

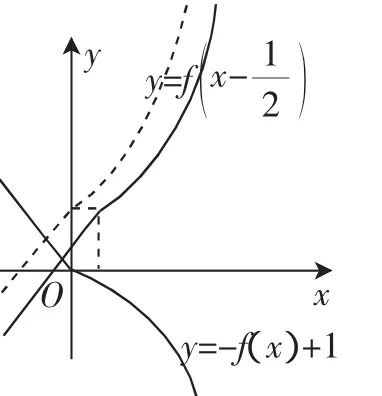
图7

评析：准确把握函数图像的变化关系，通过建立坐标系，准确作图，利用数形结合思想，有效回避了分类讨论，使问题直观获解.

“数与形本是两依倚，焉能分作两边飞，数缺形时少直观，形少数时难入微，数形结合百般好，隔裂分家万事休”.华罗庚先生之所以如此推崇数形结合思想，是因为“形”可以使某些数字问题直观化.在函数问题的处理中，将数与形进行紧密结合可找到简洁的解题途径.