高中数学思维培养之浅见

☉湖北省水果湖高中 赵 宇

高中数学思维培养之浅见

☉湖北省水果湖高中 赵 宇

爱因斯坦说：“创造性原则寓于数学之中.”今天，数学文化已成为现代科技文化的核心，它的形式化语言，理性主义观念，抽象的、逻辑的思维方式，已成为现代社会成员必备的素质.

数学是一门思维的学科，思维能力是数学学科能力的核心.数学思维，强调敏捷、灵活、广阔、深刻.与初中生相比，高中生在数学方面面临着这样一个困难的局面：更抽象的语言、更理性的思考、更庞大的知识体系，这样的难关，需要很强的思维能力才能闯过.因此，培养学生的思维能力，应该是高中数学教师最重要的使命.

在此，笔者根据自己多年的教学所得，试图总结出一些培养学生数学思维的方法，供大家参考.

一、注重激发学生的数学思维兴趣

兴趣是提高学生学习积极性的原动力，也是思维发展的前提条件.在教学中，教师可以通过一些容易让学生感兴趣的思维性问题，让他们主动动手、动脑，从而达到培养学生数学思维能力的目的.

例1 甲乙两人同时从寝室到教室，甲一半路程步行，一半路程跑步.乙一半时间步行，一半时间跑步.如果两人步行速度和跑步速度均相同，则（ ）.

A.甲先到 B.乙先到

C.同时到 D.无法确定

解析：设寝室到教室的距离为2S，步行速度和跑步速度分别为v1，v2，显然v1＜v2，则.于是

所以乙先到，故选B.

点评：本题因与学生日常生活紧密相连，所以容易引起共鸣，从而主动思考作答.

例2 某数学老师身高176cm，他爷爷、父亲和儿子的身高分别是173cm、170cm和182cm.因儿子的身高与父亲的身高有关，该老师用线性回归分析的方法预测他孙子的身高为________cm.

解析：依题意，父亲与儿子的对应数据可列表如下：

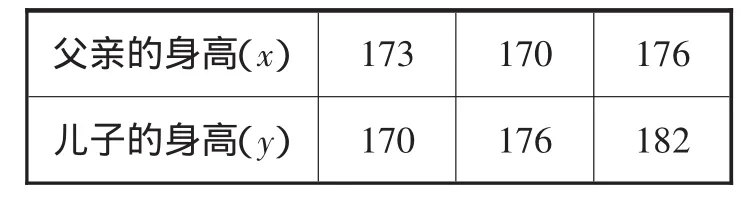
父亲的身高（x） 173 170 176儿子的身高（y） 170 176 182

则x=173，y=176，于是

所以回归直线方程为y=x+3.

从而可预测他孙子的身高为182+3=185（cm）.

点评：本题容易引起学生热烈的讨论，但对很多人而言，可能不得其门而入，主要原因是他们忽略了关键语句“儿子的身高与父亲的身高有关”，从而不能准确地列表.

二、注重学生的点滴积累

冰冻三尺，绝非一日之寒.数学思维同样不会一蹴而就，它在乎学生平时学习过程中不断地积累、沉淀、发酵.数学思维从来不排斥灵光一现，但更多地，应该是水到渠成.

例4 设a∈R，若x＞0时均有［（a-1）x-1］（x2-ax-1）≥0，则a=________.

解析：首先排除a=1，设f（x）=（a-1）x-1，g（x）=x2-ax-1，则f（x）与g（x）的图像均过定点（0，-1），欲使题中不等式成立，f（x）的图像必过g（x）的图像与x轴正半轴的交点，即（fx）与g（x）有相同的零点，即1=0，计算得a=0或，显然a=0不满足题意，故点评：本题关键在于通过数形结合来求解，注意到f（x）与g（x）的图像均过定点（0，-1）之后，一切顺理成章.如果盲目讨论，只能深陷泥泞，无法自拔.

三、注重学生数学思维的发散

上面所讲的数学思维，主要是利用已有的知识和经验及传统方法解决问题的思维方式，属于收敛思维的范畴.在高中数学学习的过程中，我们经常会遇到一些问题，用既有的思维方式难以取得突破，甚至举步维艰，此时需要我们脱离传统思维的束缚，用非常规的思维方式去寻求突破，这正是发散思维的显著特征.

例5 关于x的方程ax2+2x+1=0至少有一个负的实根的充要条件是________.

传统上，可分一正根一负根和两负根进行讨论，再加上a=0满足题意，可求得最后结果.但我们可适时提出：本着小题不大做的原则，是否可以找到一个更好的方案？经过循循善诱，最后发现可将参数a和变量x分离，将方程根的问题转化为函数值域的问题.

解析：ax2+2x+1=0⇒a=-（x＜0），所以a≤1.

点评：转化需要灵感，而灵感的来源，主要应该是扎实的基础.

例6 台风中心从A地以每小时20千米的速度向东北方向移动，离台风中心30千米内的地区为危险区，城市B在A的正东40千米处，则B城市处于危险区内的时间为多少小时？

我们来看看学生的思维过程：

（1）直观地，以台风中心为圆心，30为半径画圆，考察圆与城市B的包含情况，但因为台风中心（即圆心）在不断移动，难以把握，问题陷入僵局；（传统思维的局限）

（2）经过再思考，讨论，发现可以城市B为圆心，30为半径画圆，考察它与台风中心的包含情况，因台风中心的移动是一条连续的直线，故问题可转化为此直线与圆相交部分的长度的问题，柳暗花明.（发散思维形成突破）

解析：如图1，在△ABC中，由余弦定理可得

BC2=AB2+AC2-2AB·AC·cos45°.因为AB=40，BC=30，

所以CD=AD-AC=20，由于台风中心的速度为20，故B城市处于危险区内的时间为1小时.

图1

另解：可根据圆自身的性质，取CD中点E，连接BE，则BE⊥CD，即可求解.

点评：在本题的解决过程中，教师更适合做一个旁观者，最多给予学生适当的引导，从而让学生能自行完成思维发散的过程.

不入其门，难解个中滋味；临其境者，始觉妙用无穷.然不积跬步，无以至千里，不积小流，何以成江河？强大的数学思维能力，需要学生日积月累的扎实基础，需要学生阅尽千帆后的开阔视野，而我们教师能做的，应该就是用自己的所学、所得，把学生引进数学殿堂的思维之门.