提高数学整体与部分阅读，妙解函数的数形结合问题

☉湖南省长沙市长郡中学 王小伟

提高数学整体与部分阅读，妙解函数的数形结合问题

☉湖南省长沙市长郡中学 王小伟

数形结合法是高中数学常用的分析方法之一，也是高考必考内容之一，但不少的学生在该知识点上却得分较低，究其原因大多为读图、识图、用图能力较弱，无法实现“数”与“形”之间的转化，无法准确地完成对问题的阅读.

数形结合法可从“线”与“点”两个层面分析研究：

（1）“数形结合”指的是从整体角度利用函数图像“线”分析函数的性质及其他结论，利用数形结合法分析问题，教师一般都是从这个角度引导学生分析的.

（2）“以点为主”指的是从部分角度利用函数图像“点”分析研究图像上一些关键的点，达到分析的目的，这点容易被教师和学生忽视.

下面笔者就从高中数学在实际教学中的一些体会与做法以飨读者，供大家批评与指正.

一、研究读图类型问题

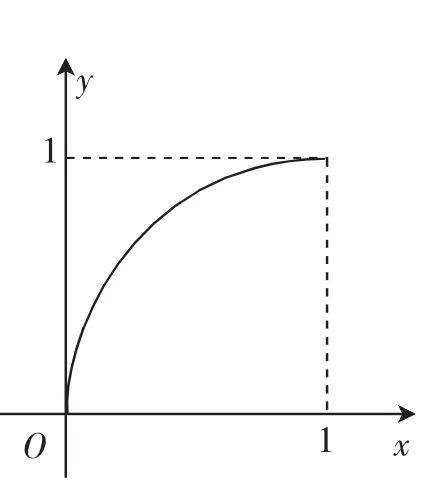
图1

例1 已知定义在区间［0，1］上的函数y=f（x）的图像如图1所示，对于满足0＜x1＜x2＜1的任意x1，x2，给出下列结论：

①f（x2）-f（x1）＞x2-x1；

②x2f（x1）＞x1f（x2）；

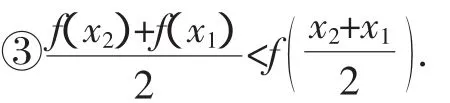
其中正确结论的序号是________（把所有正确结论的序号都填上）.

解析：“数形结合”从整体角度利用函数图像“线”分析函数的性质不易获得结论，我们可以利用“以点为主”从部分角度利用函数图像“点”分析研究图像上一些关键的点.

由图可知（0，0），（1，1）这两点连线的斜率等于1，由（fx2）-（fx1）＞x2-x1，可得，即图中任意两点（x1，f（x1））与（x2，f（x2））连线的斜率大于1，显然①不正确.

由x2（fx1）＞x1（fx2）得，即表示两点（x，1f（x1）），（x2，f（x2））与原点连线的斜率的大小，可以看出结论②正确.

任意找两点（x1，（fx1）），（x2，（fx2）），则表示两点纵坐标和的一半表示该两点中点的纵坐标，结合函数图像（图2）容易判断结论③是正确的.

图2

答案：②③

二、研究超越类型问题

1.研究分段函数问题

A.（1，10）B.（5，6）

C.（10，12）D.（20，24）

分析：“数形结合”从整体角度利用函数图像“线”绘出分段函数：（fx）=|lgx|，0＜x≤10与的图像；再根据“以点为主”从部分角度利用函数图像“点”分析研究图像上一些关键的点：（a，f（a）），（b，f（b）），（c，f（c））.

解：先绘制分段函数的图像，如图3.

图3

若a，b，c互不相等，不妨设a＜b＜c，因为f（a）=f（b）=f（c），由图像（图4）可知0＜a＜1，1＜b＜10，10＜c＜12.

图4

因为f（a）=f（b），所以|f（a）|=|f（b）|，所以lga=-lgb，即，所以ab=1，所以10＜abc＜12.

2.研究超越函数、超越方程问题

例3已知函数f（x）=|x2-4x+3|.

（1）求函数f（x）的单调区间，并指出其增减性；

（2）若关于x的方程f（x）-a=x至少有三个不相等的实数根，求实数a的取值范围.

分析：（1）“数形结合”从整体角度利用函数图像“线”分析函数图像翻折变换，“以点为主”从部分角度利用函数图像“点”分析研究图像上一些关键的点，函数f（x）=|x2-4x+3|的图像是利用f（x）=x2-4x+3的图像翻折得到的，翻折的关键先找到f（x）=x2-4x+3的图像与x轴的交点及顶点进行分析.（2）超越方程f（x）-a=x转化成部分的两个函数：f（x）=|x2-4x+3|与y=x+a.在函数f（x）=|x2-4x+3|的图像的基础上，分析直线y=x+a与f（x）=|x2-4x+3|的图像几个关键点：f（x）=x2-4x+3的图像与x轴的交点、顶点，以及直线y=x+a与抛物线y=-x2+4x-3相切的切点.

（1）递增区间为［1，2］，［3，+∞），递减区间为（-∞，1］，［2，3］.

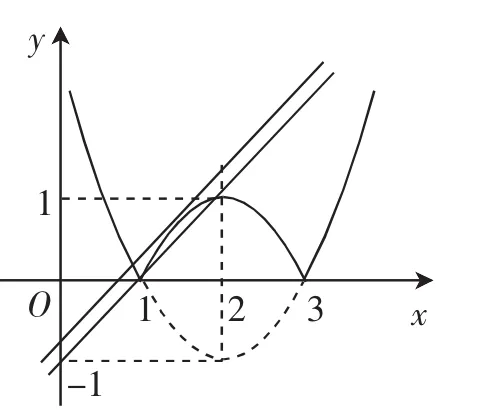
图5

（2）原方程变形为|x2-4x+3|=x+a，于是，设y=x+a，在同一坐标系下再作出y=x+a的图像，如图5，则当直线y=x+a过点（1，0）时，a=-1；当直线y=x+a与抛物线y=-x2+4x-3相切时，由3x+a+3=0，由Δ=0得.由图像知，当时方程至少有三个不相等的实数根.

3.研究超越不等式问题

例4 当x∈（1，2）时，不等式（x-1）2＜logax恒成立，求a的取值范围.

分析：超越不等式（x-1）2＜logax转化成两个函数：y=（x-1）2与y=logax.从整体角度利用两个函数图像“线”进行分析；再根据“以点为主”从部分角度利用函数图像“点”分析研究图像上一些关键的点：（1，0），（2，f（2））.

解：设y=（x-1）2与y=logax，要使当x∈（1，2）时，不等式（x-1）2＜logax恒成立，只需y=（x-1）2在x∈（1，2）上的图像在y=logax的下方即可.

当0＜a＜1时，由图像（图6）知显然不成立.

图6

当a＞1时，如图6，要使在x∈（1，2）上，y=（x-1）2的图像在y=logax的下方，只需（2-1）2≤loga2，推得1＜a≤2.

4.研究导数应用中的数形结合问题

例5已知函数f（x）=x2+bsinx-2（b∈R），F（x）=f（x）+2，且对于任意实数x，恒有F（x）-F（-x）=0.

（1）已知函数g（x）=f（x）+2（x+1）=alnx在区间（0，1）上单调递减，求实数a的取值范围；

分析：导数在应用中常见对函数零点个数、方程根的个数的研究，一般这类问题均可将超越方程或函数，利用整体或部分思想阅读并利用数形结合进行分析.

方法一：整体思想阅读：将“函数h（x）=ln（1+x2）-有几个零点？”转化成函数k与x轴的交点个数.从整体角度利用函数h（x）=ln（1+x2）-图像“线”分析图像大致草图；再根据“以点为主”从部分角度利用函数图像“点”分析研究图像上一些关键的极值点或最值点的纵坐标与x轴的关系.

方法二：部分思想阅读：将“函数h（x）=ln（1+x2）-有几个零点？”转化成两个函数y=k与y=ln（1+交点的个数.从整体角度利用两个函数图像“线”分析；再根据“以点为主”从部分角度利用函数y=图像“点”分析研究图像上一些关键的极值点或最值点与函数y=k图像的交点的个数.

解：（1）因为F（x）=f（x）+2=x2+bsinx-2+2=x2+bsinx，依题意，对任意实数x，恒有F（x）-F（-x）=0，即x2+bsinx-（-x）2-bsin（-x）=0，即2bsinx=0，所以b=0，所以f（x）=x2-2.

因为g（x）=x2-2+2（x+1）+alnx，即g（x）=x2+2x+alnx，所以

因为函数g（x）在（0，1）上单调递减，所以在区间（0，1）上恒成立.

所以a≤-（2x2+2x）在（0，1）上恒成立.

而-（2x2+2x）在（0，1）上单调递减，所以a≤-4为所求.

当x＜-1时，h′（x）＞0；当-1＜x＜0时，h′（x）＜0；当0＜x＜1时，h′（x）＞0；当x＞1时，h′（x）＜0.

如图（图7）可知：

④当k=1时，函数有三个零点.

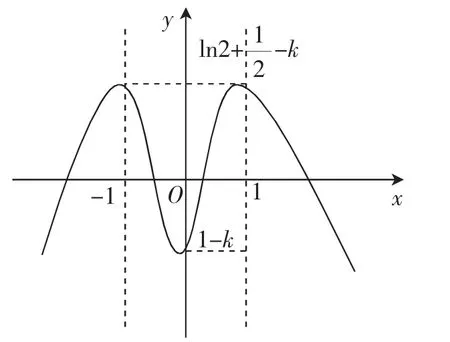
图7

当x＜-1时，y′＞0；当-1＜x＜0时，y′＜0；当0＜x＜1时，y′＞0；当x＞1时，y′＜0.

如图（图8）可知：

图8

④当k=1时，函数有三个零点.

三、体会与反思

通过以上可知函数的图像法：大体上可以根据“数形结合，以点为主”两个分析层面：

“数形结合”从整体角度利用函数图像“线”分析函数的性质以及其他结论；

“以点为主”从部分角度利用函数图像“点”分析研究图像上一些关键的点，达到分析的目的.F