分类例谈多元函数最值问题求解策略

☉浙江省宁波市北仑中学 范东晖

分类例谈多元函数最值问题求解策略

☉浙江省宁波市北仑中学 范东晖

多元函数是高等数学中的重要概念之一，随着新课改的推进，多元函数的值域与最值问题在自主招生、高考和各类数学竞赛中也常有涉及.本文就常见的多元函数最值问题的求解策略加以梳理，供参考.

一、整体换元法

整体换元就是将数学问题中某一式子看成一个整体，然后用一个所谓的”元”去代替它，再用替换了的变量根据条件去构造成新的数学关系，这样通过替换不仅可以实现数学问题的简单化，而且使得与已知条件的联系更为直观.

例1 已知实数a，b满足a2-ab+b2=3，求a2+ab+b2的最小值和最大值.

解析：将a2-ab+b2=3代入，得a2+ab+b2=（3+ab）+ab=3+2ab，下面只要求出ab的最值即可.由a2-ab+b2=3，得a2+2ab+b2=3+3ab，所以ab≥-1，当且仅当|a|=|b|=1，ab＜0时等号成立；再由a2-ab+b2=3，得a2-2ab+b2=3-ab，所以ab≤3，当且仅当a=b时取等号.于是-1≤ab≤3.

因此，a2+ab+b2的最小值是1，最大值是9.

评注：根据结论与条件中数学式子的结构特点，将条件整体代入结论表达式，尽管不能消元，但可化简所求的结论.

例2 （2015年浙江省高考题）设x，y为实数，若4x2+xy+y2=1，则2x+y的最大值是_______.

解析：令2x+y=t，则y=-2x+t，代入已知条件，并化简得6x2-3tx+t2-1=0.因为x为实数，所以由Δ=9t2-24（t2-1）≥0，得，所以2x+y的最大值是

评注：本题将要求的结论2x+y整体换元，代入已知条件，将问题转化为“方程有解需要满足的条件”来求解，这也是一种通性通法.

例3 已知x，y，z∈R+，且.求证：

即a+b+c≥9.

二、配方法

当所给出的多元函数表达式的结构具有二次关系时，可考虑配方法来解决.

例4 （2014年浙江省竞赛题）设a，b为实数，函数f（x）=ax+b满足：对任意x∈［0，1］，有|f（x）|≤1，则ab的最大值为__________.

解析：易知a=f（1）-f（0），b=f（0），则ab=f（0）·［f（1）-

例5（2007年浙江省竞赛题）设f（x，y，z）=sin2（x-y）+sin2（y-z）+sin2（z-x），x，y，z∈R，求f（x，y，z）的最大值.

评注：本题给出的式子的结构关系，利用基本不等式并不奏效，根据式中项与项之间的次数关系，我们选择了配方法.

三、不等式法

利用基本不等式（均值不等式）和柯西不等式等求解最值问题.

1.利用基本不等式

故a3b2c≤27×4.

当且仅当a=3，b=2，c=1时，等号成立.

评注：本题应用了三元均值不等式来求多元函数的最值，但要注意应用条件“一正二定三相等”.

例7 （2015年全国数学联赛题）若实数a，b，c满足2a+4b=2c，4a+2b=4c，求c的最小值.

解析：将2a，2b，2c分别记为x，y，z，则x，y，z＞0.

由条件知，x+y2=z，x2+y=z2，

故z2-y=x2=（z-y2）2=z2-2y2z+y4.

由于c=log2z，故c的最小值为

评注：本题先用换元法将已知化简，先求z=2c的最小值，进而求得c的最小值，同时要特别注意等号取得的条件.

2.利用柯西不等式

例8（2013年浙江省竞赛题）设二次函数f（x）=ax2+（2b+1）x-a-2（a，b∈R，a≠0）在［3，4］上至少有一个零点，求a2+b2的最小值.

解析：由已知得，设t为二次函数在［3，4］上的零点，则有at2+（2b+1）t-a-2=0，变形为（2-t）2=［a（t2-1）+2bt］2≤（a2+b2）［（t2-1）2+4t2］=（a2+b2）（1+t2）2.

四、数形结合法

当我们所要求的多元函数的结构式与我们学过的一些公式（如两点间距离公式、斜率公式、点到直线的距离公式、定比分点坐标公式等）的结构类似时，可考虑用数形结合的思想方法.

上题例8也可用数形结合法求解，把等式看成关于的直线方程：（x2-1）a+2xb+x-2=0，利用直线上一点（a，b）到原点的距离大于原点到直线的距离，即，接下来的解法同例8.

例9 已知实数a，b，c，d满足（b+a2-3lna）2+（c-d+2）2=0，则（a-c）2+（b-d）2最小值是________.

解析：由已知可得b=-a2+3lna，d=c+2.（a，b），（c，d）可视为平面上的两点坐标，则问题等价于求直线l：y=x+2上的点与函数y=-x2+3lnx的图像上的点距离的平方的最小值.

由图像易知，与直线l平行且与曲线y=-x2+3lnx相切的直线l0与直线l之间的距离的平方，即为所求最小值.

设切点（x0，y0），则由知，解得x0=1，所以切点为（1，-1），切线方程为y=x-2.

所以（a-c）2+（b-d）2的最小值为

评注：本题有4个参数，又夹杂着对数运算，比较难于找到问题的本质.采用数形结合的思想，把隐含的条件显露出来，使看似一筹莫展的问题柳暗花明.

五、利用函数的单调性

先将多元函数转化为一元函数，然后利用函数的单调性来确定最值.

例10设0≤x≤π，0≤y≤1.试求函数f（x，y）=（2y-1）sinx+（1-y）sin（1-y）x的最小值.

解析：由题意易知，对一切0≤x≤π，有sinx≥0，sin（1-y）x≥0.

，有tanx＞x＞sinx，

且sin（x+δ）=sinx·cosδ+cosx·sinδ≤sinx+δcosx.

则

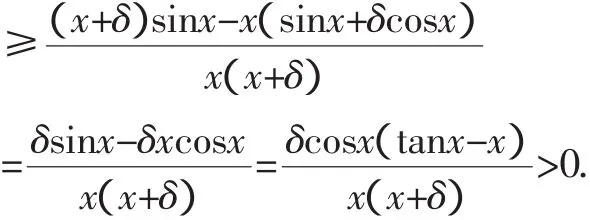
又因为0＜（1-y）x≤x≤π，

注意到（1-y）2=1-2y+y2≥1-2y＞0，

故（2y-1）sinx+（1-y）sin（1-y）x≥0，即f（x，y）≥0.

当y=0时，等号成立.

综上，当x=0或y=0时，f（x，y）min=0.

六、赋特殊值法

有些竞赛题直接解答有难度，不妨“退后一步”，从特殊出发，先探索出结论，再证一般性.

设x-2=cosθ（θ∈［0，π］），则

设g（x）=x3-ax2-bx-c，在区间［1，3］上，关于x=2对称地取值

则

七、逐步调整法

例12 （北大自主招生题）已知a1+a2+a3=b1+b2+b3，a1a2+a2a3+a3a1=b1b2+b2b3+b3b1，若min（a1，a2，a3）≤min（b1，b2，b3）.

求证：max（a1，a2，a3）≤max（b1，b2，b3）.

证明：不妨设a1≥a2≥a3，b1≥b2≥b3，条件为：a3≤b3，

要证：a1≤b1.

由假设可知α≥β.

若α=β，则a1+a2=b1+b2，a1a2=b1b2，从一元二次方程根的角度可知，a1=b1.

若α＞β，因为a1a2+a2a3+a3a1=b1b2+b2b3+b3b1，所以

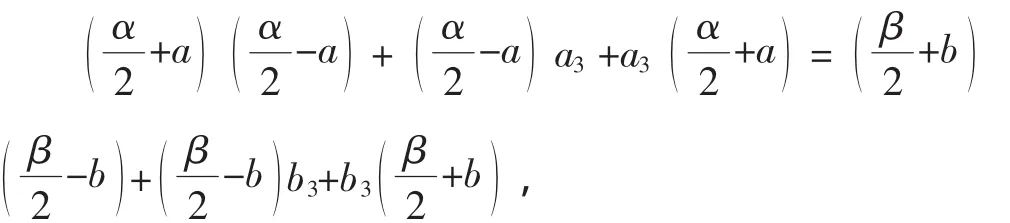
评注：本题采用分析法、换元法解决，利用式子的轮换对称，假定字母的大小顺序，从而产生分析法的思路.

最后指出，求解多元函数的最值问题，除了上述方法外，还有减元法、判别式法、分类讨论法等，有时还需要多种方法的综合运用.由于篇幅所限，这里不再一一举例.