类比中获新知 应用中显能力——从高中数学类比法解题谈起

☉湖南省隆回县第一中学 王一帆

类比中获新知 应用中显能力
——从高中数学类比法解题谈起

☉湖南省隆回县第一中学 王一帆

在现行的高考制度下，高中数学学科具有十分重要的地位，学生的数学解题能力是数学教师和学生都关注的焦点；实践表明，在高中数学各级各类质量检测中，解题能力强的学生都能取得较高的分数；值得我们注意的是：数学思想方法的灵活运用是提升数学解题能力的重要保障；类比是一种数学思维方式与解题思想，在高中数学中主要涉及“概念、结构、次数、元数、方法”的类比，本文借助于典型案例的剖析，重点从“平面与空间、椭圆与双曲线、低次与高次、少元与多元”等四个方面的类比进行探究，充分展现类比法在高中数学解题中的优越性与实效性，仅供参考，若有不当之处，敬请批评指正.

一、平面与空间问题的类比

在高中数学知识中，平面上涉及“点、线、面”，空间上涉及“线、面、体”，这些对应的元素，往往存在一定的数学类比关系，也是专家进行探究创新命题的素材；在几何问题中，出现一种新的题型：“根据平面几何的性质类比到空间问题之中，猜想、探究空间结构图形中也满足其性质特点”.

例1 已知O为△ABC的内切圆的圆心，AB=c，AC=b，BC=a，存在面积等量关系：S△OAB+S△OBC+S△OCA=S△ABC，则可得到△ABC的内切圆半径；若将此平面三角形几何性质类比至空间三棱锥问题中，即在三棱锥DABC中，S△ABC=SD，S△BCD=SA，S△CDA=SB，S△DAB=SC，试求：三棱锥D-ABC的内切球的半径R的值.

剖析：平面三角形中，S△OAB+S△OBC+S△OCA=S△ABC，即，即；空间三棱锥中，令P为三棱锥的内切球的球心，存在体积关系V三棱锥P-ABC+V三棱锥P-CDA+V三棱锥P-BCD+V三棱锥P-DAB=V三棱锥D-ABC，即，即R=

点评：本题是根据平面几何中存在的性质拓展类比至空间结构中，给学生探索、猜想的平台，题中主要是根据“平面中的面积和”与“空间中的体积和”进行拓展类比，不仅考查学生类比联想和空间想象的能力，更加注重学生逻辑推理和创新能力的考查与培养，符合新课改的主导思想.

二、椭圆与双曲线问题的类比

在高中数学解析几何问题中，椭圆和双曲线是考查的重点之一，两者之间存在一定的联系与区别，若能搞清两者之间的区别和联系，有助于提升解决此类问题的效率.

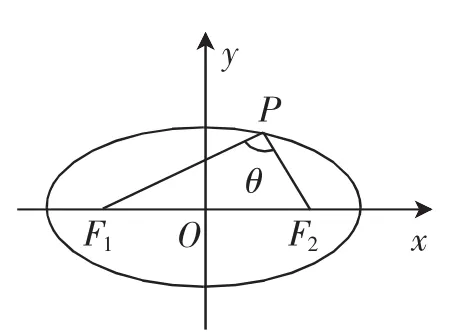
图1

图2

剖析：根据题意，构建如图2所示双曲线，令∠F1PF2=θ，|PF1|=m，|PF2|=n，则存在m-n=2a，4c2=m2+n2-2mncosθ，则，则可得到双曲线焦点三角形面积的计算公式为

点评：本题主要探究椭圆和双曲线的焦点三角形面积问题，椭圆中与双曲线中两个表达式结构十分相似，充分说明圆锥曲线中椭圆与双曲线的本质规律的一致性，本题侧重于计算椭圆与双曲线焦点面积公式形式上的类比，有助于提升学生的逻辑推理能力.

三、低次与高次问题的类比

在高中数学的代数问题中，不等式的性质和不等式的应用是高考的重要内容之一，在含有字母参量的不等式中，若增加参量方根的次数可能会大大增加表达式的复杂性，但高中数学中的不等式问题含有一定的规律性，这是值得大家注意的地方.

例3 高中数学不等式章节中存在这样一个性质：“两个正数a、b的算术均值的平方小于等于其平方的算术平均值”，即且a=b时不等式中等号成立），其证明过程为，即可证明上述不等式性质成立；若增加参量的次数为3时，请根据不等式特征进行类比，写出猜想的结论并加以证明.

剖析：根据参量次数是2时的特征，比较容易猜想次数为3时不等式性质表示形式为R+且a=b时不等式中等号成立），则

点评：本题中含有正参量的不等式性质直接源于课本中，多数学生十分熟悉，题设部分展示其证明过程，要求学生根据结构特征进行类比，推广两个参量的次数，可以得出结构相似的新结论，题中已经证明了次数为3时的正确性，对于心有余力的学生而言，这里可以进一步拓展次数增加4、5、…时，得出的新结论是否正确，并加以逻辑证明.

四、少元与多元问题的类比

不等式问题是高考的必考内容，不等式的考查形式呈现多样化，不等式证明题是考查的重要形式之一，常规不等式题型中参量的元数通常是保持不变的，若增加参量的元数则难度加大，对学生的理解运用能力要求高.

剖析：根据题设呈现的不等式中三元对应三个具有“特色”分式形式，若由3个元数增加至4、5、6、…、n个元数时，不等式形式变为.此不等式证明如下：当n=3时，根据题设信息可知成立，假设n=k（k≥3）时，不等式成立，则当n=k+1时，存在不等式成立，则当n≥3时，类比猜想的不等式成立.

点评：本题是基于不等式问题，由三个字母参量的大小关系，得出“特殊”的分式不等式关系，再由三元拓展至多元，猜想得出新的不等式形式，采用数学归纳法对猜想内容进行证明与验证，侧重于考查学生拓展思维、猜想推理能力，在完成题目的一系列过程中体会类比思想方法在处理高中数学问题中的优越性和独特性，同时激发学生探索新知的欲望.

总之，数学思想方法是解决高中数学问题的重要途径，类比思想方法在解题中的有效运用有助于提升学生数学解题能力，让学生在联想、类比、拓展中不断提升发现问题、提出问题、解决问题的能力，让学生亲身经历数学知识、数学能力和数学素养“点→线→面→体”的逐步升华过程，感悟类比数学思想方法的“独特”魅力.F