论数学方程思想对高中物理解题的重要性

许军　何蓉

摘 要：数学与物理在方法和思想方面有着不可分割的联系，数学不仅是物理学科的基础，它也是很多物理问题解答的桥梁。尤其是数学方程思想，它不仅在代数和几何学科中被广泛应用，也常应用于其他学科，如物理学科。所以，本文在简要阐述方程思想的含义及对高中物理解题的重要性的基础上，着重分析了应用方程思想来解答高中物理常见的几类典型实例，并提出在解决物理问题时应用数学方程思想的建议，以此来帮助学生看透解题的本质并引导学生善于应用数学方程思想解题，让高中物理问题在方程思想中迎刃而解。

关键词：方程思想；高中物理；重要性；解题

【中图分类号】G 【文献标识码】B 【文章编号】1008-1216（2017）08B-0104-02

一、数学方程思想

关于方程思想的含义，不同的研究者在各自研究中有过不同的阐述。张奠宙和张广祥认为方程思想就是通过构建已知量与未知量的关系而进一步探讨求出未知量的方法。简而言之，就是建立已知与未知之间的桥梁。人们通常会认为方程就是方程思想，可两者之间既有区别又有联系。方程属于知识体系，而方程思想是属于思维体系。当然，方程思想的形成是根据物理量与量之间的关系，构造方程或方程组，再解出未知量。利用方程思想解决问题，首先需要分析已知量和未知量之间的关系，其次根据问题中的数量关系构建含有未知数的方程或方程组，最后根据方程或方程组的变形求出未知数的值。培养学生善于利用方程思想解题，这不仅能够激发学生学习的兴趣，也能培养学生建构模型的能力。

二、用方程思想解答高中物理题的实例

在高中物理解题过程中，使用方程思想解答物理问题的实例不胜枚举，本文主要从高中物理力学和电磁学两个方面来加以说明。

（一）力学

高中物理力学主要包括运动学、动力学以及静力学，并且已经形成了严密的逻辑体系，比如，运动学部分，从直线到曲线，由匀速到变速，从运动规律到具体分析都有严密的体系以及科学推理过程。同时，牛顿第二定律、动量定理、动量守恒、动能定理、机械能守恒都有严密的逻辑体系。此外，高中物理在定量计算方面相比于初中所学内容较复杂，几乎每部分都与方程相关，如建构方程等式、如何解方程以及对解的验证与分析，这对高中生来说既是困难，也是挑战。

【例1】A、B两物相距为x，它們同时同向运动，B在A前面做初速度为0，加速度为a1的匀加速直线运动，A在后面做初速度为v0，加速度为a2的匀加速直线运动，则（ ）

A、若a1 = a2，它们只能相遇一次

B、若 a1>a2，它们可能相遇二次

C、若a1>a2，它们只能相遇二次

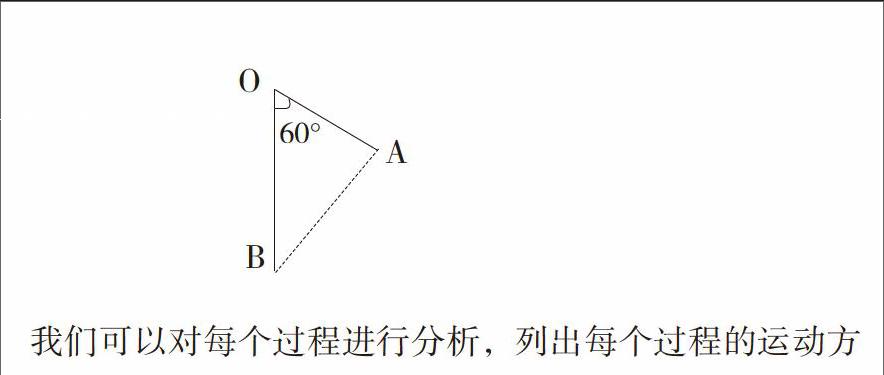
D、若a1

解析：对于此题，我们采用方程思想求解，设经过时间t以后两物体相遇，抓住题中关键字“相遇”，可以得到位移相等的关系，结合运动学位移——时间公式列出等式方程：a1t2+x=v0t+a2t2，经过整理得到（a1-a2）t2-2v0t+x=0；显然，这是关于t的方程；当a1=a2时，为数学形式的一元一次方程，t仅只有一解，即相遇一次；当a1≠a2时，为一元二次方程，依据?=4v02-4x（a1-a2），当 a1>a2时，?可能大于零，从而t可能有两解，由韦达定理可知两解为正，即可能相遇两次，当a1

实际上，运动学部分有关于初速度为零的匀变速直线运动规律的一些推论，也是利用速度关系或者位移关系建构物理等式方程，然后对其求解，得到相应的结论。

（二）电磁学

如果说力学是物理学的基石，那么电磁学就是物理学的支柱，一般来说，力学和电磁学是中学物理最重要的两部分内容。电磁学主要分为电场、磁场以及电磁场，每部分都有各自的严密体系以及内在逻辑，同时电磁场之间又是相互关联，由麦克斯韦方程组可直观了解。但这部分定性分析以及定量求解对高中生的要求较高，同时这部分内容与数学方程联系更为紧密。

【例2】如图，O、A、B为同一竖直平面内的三个点，OB沿竖直方向，∠BOA=60°OB=OA，将一质量为m的小球以一定的初动能自O点水平向右抛出，小球在运动过程中恰好通过A点。使此小球带电，电荷量为q（q>0），同时加一匀强电场，场强方向与 所在平面平行，现从O点以同样的初动能沿某一方向抛出此带点小球，该小球通过了A点，到达A点时的动能是初动能的3倍；若该小球从O点以同样的初动能沿另一方向抛出，恰好通过B点，且到达B点的动能为初动能的6倍，重力加速度大小为g。（2014年全国卷Ⅰ卷25题）

求：该电场强度的大小和方向。

解析：如果从方程的角度去思考该问题，就更易解答。对此进行分析：

我们可以对每个过程进行分析，列出每个过程的运动方程：

从O点到A点，没有加电场时，列出动能定理方程：

mgOAcos60°=mvA2-mv02=EKO （1）

加电场后通过A点列出动能定理方程：

mgOAcos60°+qUOA=mvA'2-mv02=2EkO （2）

加电场后恰好通过B点，列出动能定理方程：

mgOB+qUOB=mgOA+qUOB=mvB2-mv02 （3）

通过（1）（2）（3）式可以解得UOA、UOB与EkO之间的关系，进而确认UOA、UOB之间的比例关系，后面的计算更为清晰。

通过力学和电磁学两部分例题了解到，数学方程思想在高中物理解题中具有重要地位。方程思想主要有构建方程、方程变形、解方程以及运用数学方法处理方程。所以，在高中物理解题中培养学生应用数学方程思想显得尤为重要。

三、应用数学方程思想的几点建议

（一）根据物理量与量之间的关系建构方程

实际上，很多高中物理题在定性分析时较难把握，若以方程形式表达则物理量的关联性、物理规律就会逐渐变得细微。正如华罗庚所说的“数缺形时少直观，形缺数时难入微”，物理习题中的多数运算过程较为抽象，如果應用数学方程，定性分析和定量计算就会较易把握。

如何培养学生建构方程的能力，是解答高中物理题的重中之重。首先，培养建构物理方程能力需要教师和学生的双向合作，教师需要保证学生以物理学习心理为基础，在学生已有的数学方程基础上，举例说明如何将数学方程建构应用到物理题中。其次，建构物理方程需要学生有较好的知识迁移能力。由迁移理论可知，不仅数学方程可以部分运用到物理习题中，而且数学上有关如何建构方程的思想也可以迁移到建构物理方程过程中。所以，要注重提高学生的知识迁移能力。

（二）对已建构方程变形并求解

关于方程的变形和求解，很多中学老师百思不得其解为什么学生掌握了如何建构方程，却在方程变形与求解过程中遇到困难。其实，这些困难有其出现的必然因素。根据教学观察发现有以下几点原因：第一，运算能力较差：在教学过程中发现现阶段很多中学生都依赖于计算器，甚至连小学生也都纷纷借助计算器解题；长久的依赖势必减弱学生对数字和代数的敏感度，从而导致学生在方程的变形与求解过程中耗时大，还易出错；第二，解方程时，方法选择具有盲目性。很多学生在解方程过程中出现思维固化，如上文例1中问及“相遇”情况，笔者在教学过程中发现多数学生是按部就班的解出一元二次方程，再对方程的解进行分析。再如上文例2，对于已建构的（1）（2）式若采用代入消元法，会使解方程更复杂；若采用数学中的加减消元法会使解的过程更为轻松。

综上所述，如果要使我们的物理方程解得更快、更准确，需要做到以下几点：第一，摆脱计算器，多用笔算，逐渐产生对数字和代数的敏感性；第二，打破思维僵化，对于具体方程需要先观察，尽可能避免做无用功，这样可大大节省答题时间，这也是解答物理题非常重要的环节。

参考文献：

[1] 张奠宙，张广祥.中学代数研究[M].北京：高等教育出版社，2006.

[2] 史宁中，濮安山.中学数学课程与教学中的函数及其思想——数学教育热点问题系列访谈录之一[J].课程·教材·教法，2007，（27）.

[3]崔声隆.函数与方程思想在求数列通项中的应用[J].福建教育学院学报，2014，（2）.

[4]张娟.初中学生对方程思想的理解[D].华东师范大学，2007.

[5]张荣奎.高中物理教学培养学生应用数学能力的方法与实践[D].山东师范大学，2014.

[6]张亚金.新课程标准下物理教学中渗透数学思想方法的探究[D].上海师范大学，2009.endprint