怎样解题*——从三角形的内角和说起

●王 强

(钟英中学，江苏 南京 210002)



怎样解题*
——从三角形的内角和说起

●王 强

(钟英中学，江苏 南京 210002)

当遇到一个新的问题时，首先可以从特殊情形出发猜想出结论，并提炼出解决问题的方法，然后回到一般情况下，猜想结论是否成立并给出验证；其次可以将问题的条件一般化，从而推广结论，或者将问题的条件特殊化使得结论得以加强.这就是波利亚《怎样解题》中特殊化与一般化的解题方法，值得每一位教师和学生学习.

怎样解题;一般化;特殊化

1 背景描述

江苏省南京市秦淮区中学数学教研室开展以学习波利亚《怎样解题》中的思想方法为纲领，在各个年级开展“怎样解题”活动.笔者有幸在初一年级开展此研究课，基于初一学生“知识储备少，数学思维能力弱”的前提，从最基本的动点问题渗透解题教学中“特殊与一般”的思想方法.当遇到一个问题无从下手时，可以从最特殊的情形出发，得出特殊情形下的结论，基于特殊情形下的结论猜想出一般情形下的结论，再通过证明验证结论，这是数学研究最自然的办法之一，同时也是解题教学中的重要方法之一.

正如波利亚所说：“没有一道题目可以解决得十全十美，总存在值得我们探究的地方.”我们继续研究解题，然后将问题条件一般化；或者将问题条件特殊化，加强结论，最终从特殊走向一般的是要教会学生解题方法.

2 课堂实录

环节1 回顾三角形内角和定理——明确特殊与一般的思想方法.

师：请同学们来复述一下三角形的内角和定理.

生1：三角形的内角和是180°.

师：你能否通过一些特殊的例子得到三角形的内角和是180°?

生2：一副三角板的3个角分别是30°，60°,90°或45°,45°,90°，内角和是180°.

生3：可以通过将△ABC的顶点A压缩至边BC上，这时可以发现∠B，∠C都是0°，而此时的∠A的度数是180°，通过这个特殊的位置猜测出三角形的内角和是180°.

生4：也可以通过将边BC无限地缩小，会发现此时∠A接近于0°，∠B与∠C的度数都接近于90°，此时也可以猜测出三角形的内角和是180°.

师：这3位同学讲得很好.通过将几何图形经过适当变形之后，也就是我们通常所说的图形特殊化后，可以得到一个结论，这个结论也许就是在一般情形下的答案.这样一种研究解题的方法就是美国著名数学教育家波利亚提出的“特殊与一般”方法.正如哲学家康德所说：人的认识从感觉开始，再从感觉上升到概念，最终形成思想.今天，老师将带领大家用这样一种办法来研究怎样解题，体验特殊与一般的魅力.

思考 生3的回答是源于苏教版教材七年级下的阅读材料，之前学习三角形内角和内容时已经让学生自己阅读过，在上公开课时学生能想到此方法，说明学生对于特殊化思想还是有印象的，生2的回答是特殊化的具体表现.在课堂中，生4的回答让我们感到很“惊艳”，笔者之前也没有想到这个办法，说明只要引导到位，自然生成总是那么自然.

环节2 经典例题探究——特殊中见一般.

题目 强老师给爱好学习的小茗同学提出这样一个问题：

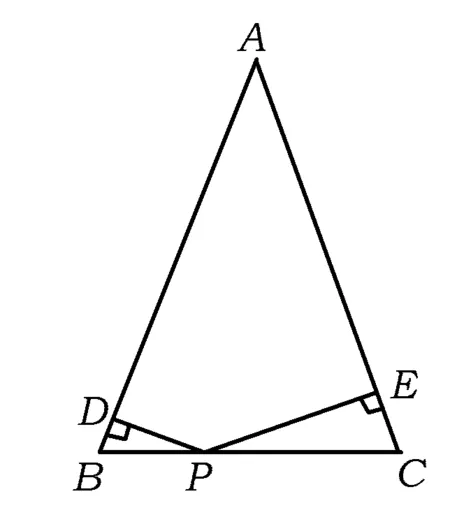
图1

如图1，在△ABC中，AB=AC，点P为边BC上的任意一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D,E,则PD+PE等于三角形中哪条线段的长？

学生陷入思考.

生5：老师，凭我的感觉，应该是AB边上的高.

师：你是怎么想到的？

生5：根据刚才您说的办法，由于点P是BC上任意一点，我把点P的位置特殊成点C，此时PD+PE就是点C到AB的距离.

师：这个想法很好，假设点C到AB的距离是CG，下面我们尝试证明这个结论.

教师板书：PD+PE=CG?并给学生3分钟时间思考，然后巡视，大约有5人做出这道题目.

师：大家思考一下，点P除了可以特殊化成点C，点P在边BC上还有什么特殊位置？

生(大部分学生)：中点.

师：中点让你联想到了什么？

生6：老师，点P是中点让我想到了中线AP，此时△ABP与△ACP的面积相等，都等于△ABC的面积一半.

师：说得非常好.(停顿两秒)如果点P不是中点，那么在移动过程中，△ABP与△ACP的面积有什么关系？有没有不变的量?

短暂停顿后，教师看到学生恍然大悟的表情，大约2分钟后班上多数学生找到了解题思路.

师：请同学们来讲讲如何思考？

生6：联结AP，由S△ABC=S△ABP+S△ACP，易得结论.

师：回答得很精彩，掌声鼓励.我们发现S△ABC=S△ABP+S△ACP，这个方法很好，这是我们俗称的“等面积法”，大家注意提炼题目中的“变与不变”.PD+PE等于点C到AB的距离是怎么算出来的？

生7：因为AB=AC，在上述的等式两边同时除以AB，可得要求的结果.

思考 这个环节是本节课的第一个难点，题目的结论是开放性的，需要学生猜测出结论，而猜测出结论就需要将点P移动到两个端点处，得到PD+PE是腰上的高.从课堂效果看，这个结论对于学生来说相对简单，至于结论是否正确需要我们去验证.引导学生将点P特殊化成中点的目的是提示他们得到面积相等，以及联结辅助线AP的做法，从而在任意的点P处想到联结AP，寻找在此过程中的变与不变，其中S△ABP+S△ACP的值不变.此题解决的另一个关键点是△ABC是等腰三角形.

环节3 问题拓展——从特殊走向一般再走向特殊.

师：正如美国著名数学教育家波利亚所说：没有一道题可以解决得十全十美，总存在值得我们探究的地方.刚才我们研究的点P是在线段BC上的一个动点，点P还可以在什么位置？

思考片刻，学生小组之间交流.

生8：如果点P不在BC上，可以在三角形内部，把点P放在△ABC的内部.

生9：点P也可以在BC的延长线上.

生10：点P也可以在△ABC的外部.

师：关于点P的位置，除了在线段上，也可以在BC的延长线上，也可以在三角形内部、三角形外(板书)……，我们先来研究一下点P在线段BC的延长线上，然后再探究点P在三角形内部时，PD，PE和CG的数量关系.

拓展1 强老师给爱好学习的小茗同学又提出这样一个问题：如图2，在△ABC中，AB=AC，点P为BC延长线上的任意一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D,E,则PD,PE,CG三者有何关系？

师：请大家将PD,PE画出来，并思考此时PE是哪个三角形的高?

请学生上黑板板演(5分钟)，教师巡视.

生11：PE是△APC的高，可以发现S△ABP-S△ACP=S△ABC,故PD-PE=CG.

师：讲得真好，依然用等面积法，只不过此时面积最大的三角形是△APB.

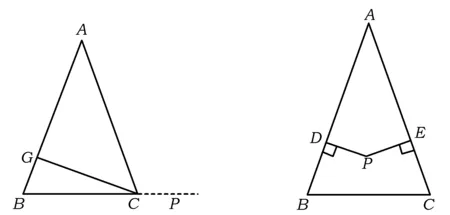
图2 图3

当点P为△ABC内任意一点时,又可以得到：

拓展2 强老师给爱好学习的小茗同学再提出这样一个问题：如图3，在△ABC中，AB=AC，点P为△ABC内任意一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D,E,则PD+PE等于三角形中哪条线段的长？

生12：等于CG.

生13：肯定不等于CG，若点P靠近点A时，发现线段和接近于0，但点P靠近点C时，线段和接近于CG的长度.

师：讲得好，这就是我们不久前学习过的举反例，精彩，完美！

生14：如果点P在三角形内部，可以发现S△ABC≠S△ABP+S△ACP，因此点P在内部是不行的.

生15：把△PBC的面积加进来，添加辅助线PF⊥BC于点F，就可得PD+PE+PF和CG之间的关系.

生16：虽然S△ABC=S△ABP+S△ACP+S△BCP，但是由于AB≠BC，不能同除以AB，没有办法继续做下去，因此将点P放在三角形内部不合适.

师：讲得很有道理，这就是举反例的魅力啊!那么在什么情况下，PD+PE+PF可能会等于CG?

生：等边三角形.

思考 在这个环节，笔者的上课过程明显感到很顺畅，师生互动较好，许多问题迎刃而解.特别地，我们将一个问题条件进行改编，有时问题的结论依然成立，有时问题的结论并不成立，但将点P放在三角形内，通过特殊化点P的位置易得PD+PE的长度跟腰高没有关系.有学生想到了这题的本质是面积的和差，想到添加△PBC的面积，但依然解决不了问题，此时将等腰三角形改成等边三角形就很自然了.问题改编的思路是将条件特殊化，最终的结论将变得更强.

环节4 深入剖析——方法迁移一般化.

师：回顾刚才的拓展2，不能继续做下去的原因是不能同除以AB或者BC，若AB=BC，则有：

拓展3 如图4，已知点P为等边△ABC内任意一点，自点P向3条边作垂线PD,PE,PF，点D,E,F分别为垂足，探究PD+PE+PF与△ABC高的关系？

生17：由于S△ABC=S△ABP+S△ACP+S△BCP，因此PD+PE+PF=h，其中h是三角形的高.

师：同学们，我们发现了这么漂亮的一个等式，h是任意边上的高，由于△ABC是等边三角形，因此各边上的高都相等.那你有没有想过若一个三角形的3条边不相等，是否也有类似的结论呢？

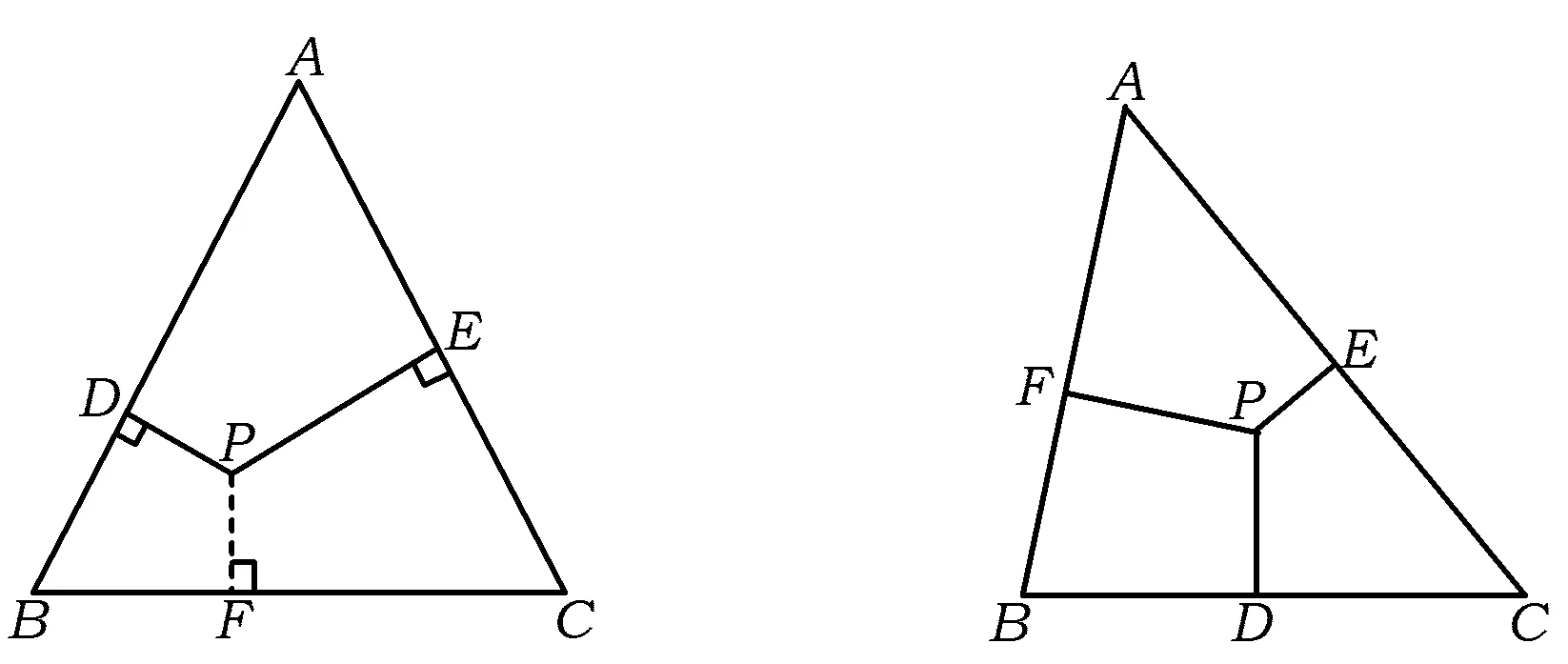
图4 图5

拓展4 如图5，已知点P为任意△ABC内任意一点，自点P向3条边作垂线PD,PE,PF，点D,E,F分别为垂足，探究PD,PE,PF与△ABC高的关系？

师：拓展4留作大家课后思考，下面请同学们回顾这节课所学的内容？

生18：今天我们学习了特殊与一般的方法，可以将问题特殊化之后，猜想结论，最终证明结论.

师：很好.我们首先将问题特殊化，在特殊中见一般；然后在拓展中一般化和拓展中特殊化；最终形成方法迁移的一般化.也就是今天这节课中特殊与一般的解题思想.

3 教学分析

3.1 基于教学内容的思考

本节课以学生熟悉的等腰三角形的高为载体，运用“特殊与一般”的思想方法，教师主导和学生主体建构的教学手段和“等面积法”应用贯穿始终，引导学生经历整个探究的过程.例题中联结AP是这道题目的难点，笔者通过试讲发现这条辅助线对学生来说是一个障碍，因此教师主导的地位应发挥作用.通过不断引导、思考、设问、思考、追问、讨论，提示学生找到中点P这样一个特殊位置，发现中点P与中线AP之间的密切联系，以及过点P向两腰作垂线，找到了点P在变化过程中的不变——面积.

考虑到对初一学生而言，做钝角三角形的高也是难点，拓展1也仍然是开放性问题，果断地加入画高环节，体现了“做中学”的想法，笔者认为这是本节课中的亮点之一.对于点P为△ABC内任意一点，探究PD+PE与CG的关系，我们通过举反例将问题巧妙解决，但在解题过程中，不满足结论到此为止，适当增加了辅助元素，将题目的条件进行加强，得到更加精美的结论，如拓展3，鉴于时间原因未能完成拓展4，是这节课的一个遗憾.

3.2 基于数学思想的思考

数学思想方法是基于先前的基本活动经验，在实践中不断地思考与回顾，形成自己的解题感悟与方法.而学生只有经历了探究的过程，才知道哪里是真正的难点和突破口，最终形成思想.本节课是基于波利亚怎样解题策略中的“特殊与一般”的思想，整节课从特殊到一般，猜想结论，从而证明结论，或者通过举反例将结论否定，整条主线脉络清晰.

3.2.1 几何图形的一般与特殊化

平面几何图形由点线构成，几何体由点线面构成,这些属于基本要素.而从平面图形到立体图形就是一个一般化的过程.研究三角形从一般的三角形入手，到等腰三角形最终到等边三角形；从一般的四边形到平行四边形到菱形或矩形，最终到正方形的研究，都是基于一般到特殊的研究.因此方法的研究便可以迁移了，例如从一般的多面体到特殊的多面体；研究三角形三边之间的关系，两边之和大于第三边，两边之差小于第三边；初中阶段最容易想到的直角三角形勾股定理.

3.2.2 代数推理的一般与特殊化

例如我们研究(a+b)2，其实就是(a+b)(c+d)的特殊形式，因此乘法公式就是一般多项式乘法基础上研究特殊多项式的乘法.基于(a+b)2的研究顺利地过渡到(a+b)3，最终到达(a+b)n的研究，这就是高中所学的二项式展开定理.初中阶段推导基本不等式，都是先通过举一些具体的数字代入，比较a2+b2和2ab的大小，最终猜想出结论a2+b2≥2ab，最终通过完全平方公式进行证明.高中阶段学习的椭圆、双曲线、抛物线的概念可以转化成为动点到定点的距离和定直线的距离，俗称圆锥曲线的统一定义，这也是从特殊到一般的生成.

3.2.3 函数研究的一般与特殊化

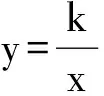
3.2.4 点线面位置关系的一般与特殊化

苏教版教材七年上册研究“平面图形的基本认识”中提到两条直线的平行与垂直关系，高中阶段加入两条直线异面的位置关系，引入两条直线夹角问题.从线面的位置关系联想到面面位置关系，面面平行、面面垂直、以及面面形成的二面角问题，都是从特殊到一般的发展，有一定的研究意义.

无论是在教学内容上的思考，还是在思想方法上的反思，解题教学一定要基于“理解数学”这个前提.只有理解了数学，才能更好地理解学生和理解教学，这其中“特殊与一般”的思想方法应用相对较多，我们要引导学生学会思考，最终让学生从“怎样解题”到“学会解题”.

�2017-04-18；

2017-05-21

江苏省南京市教育科学十三五规划个人课题“波利亚的怎样解题策略在数学教学中的应用”(Dc1846)

王 强(1987-)，男，江苏南京人，中学一级教师.研究方向：数学教育.

O123.1

A

1003-6407(2017)08-16-04