例题的选取、变式及拓展——以“解三角形”和“空间几何体的表面积及体积”为例

●

(象贤中学 广东广州 511483)



例题的选取、变式及拓展
——以“解三角形”和“空间几何体的表面积及体积”为例

●李伟

(象贤中学 广东广州 511483)

好的例题教学要教会学生“以不变应万变”“以少驭多”，这就需要选择的例题、变式及拓展是恰当的、有效的.在此，以“解三角形”及“空间几何体的表面积及体积”为例，具体阐述了例题、变式及拓展的小单元整体设计过程，为好的例题教学奠定了基础.

例题教学；微专题；解三角形；空间几何体

1 问题背景

数学高考备考是一个永恒的话题，从市、区、校各级教育行政部门到一线教师，都在想办法、找抓手，尽最大可能提升备考效果.如广东省广州市教育研究院提出了“抓基础、抓重点、抓落实”“精选材料、分层落实、有效训练、及时反馈”的高考备考策略，广州市番禺区教研室提出“强化例题教学”，把广州市的备考策略落到实处.对于例题教学，首要条件是选好题，这是“好的例题教学”的保障.

2 观点及方式

“好的例题教学”要教会学生“以不变应万变”“以少驭多”，这就需要所选择的例题、变式及拓展是恰当的、有效的.笔者认为：例题、变式及拓展是相辅相成的整体，都是为实现例题教学的目标服务的,不要刻意去区分它们，但需要了解一些基本的原则及方法，而且这些变式、拓展还可以作为一种策略性知识让学生学习，从而提升学生的数学核心素养.

对于例题的选取，要注意以下两个原则：

1)目标定位，分层落实.实质上，在高考备考阶段，由于知识的综合性，例题已不再是单个的例题，更应是一个例题组，或者说是一个微专题.

2)入口宽泛，思维发散，按需拓展.这也是例题教学能够达到“以少驭多”功效的一个根本原因.

例题的变式可以对问题的条件、结论进行不同的表征，也可以把问题的条件、结论交换位置等；例题的拓展有多种方式，如将静态问题拓展为动态问题，将数学问题拓展为应用类问题，将封闭型问题拓展为开放型问题.

例题、变式及拓展的题目选取恰当，能帮助学生更好地认识问题本质，更快地形成新认知结构[1]，从而提升学生的解题能力.

3 案例及解读

案例1“解三角形”的求值问题

用正、余弦定理求三角形边和角的值，实质上是已知3个量求另外3个量的问题.问题的核心在于这3个量能否明确、能否分层落实.此类问题可设计3层目标：1)已知3个量，直接运用；2)已知两个量，第3个量从外界获得；3)已知两个量，求取值范围.此3层目标有一定的递进关系，现分别给以具体论述.

1)已知3个量，直接运用.

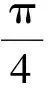
拓展在平面四边形ABCD中，∠A=∠B=∠C=75°，BC=2，则AB的取值范围是______.

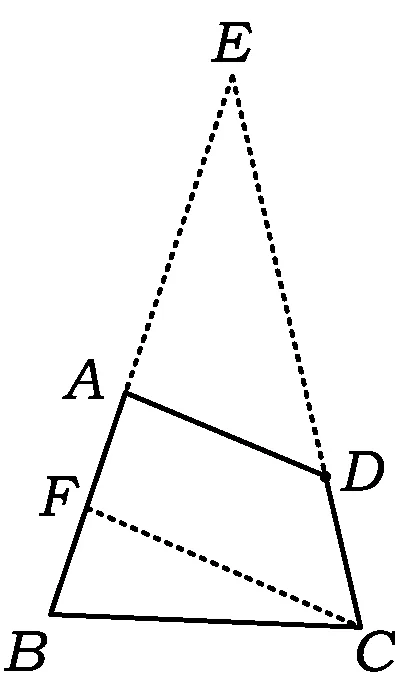
图1

(2015年全国数学高考新课标卷Ⅰ理科试题第16题)

分析如图1，随着点A的变化(在BE上运动)，平面四边形ABCD存在两个临界状态[2]，△FBC为最小临界，△EBC为最大临界.

设计意图例1是正弦定理的直接应用；变式把边c用S△ABC=2这种形式来表征；拓展把两个临界状态的确定三角形与动态的平面四边形做了无缝连接，在体会高考试题设计精妙的同时，深刻理解问题的本质.

2)已知两个量，第3个量从外界获得.

图2 图3

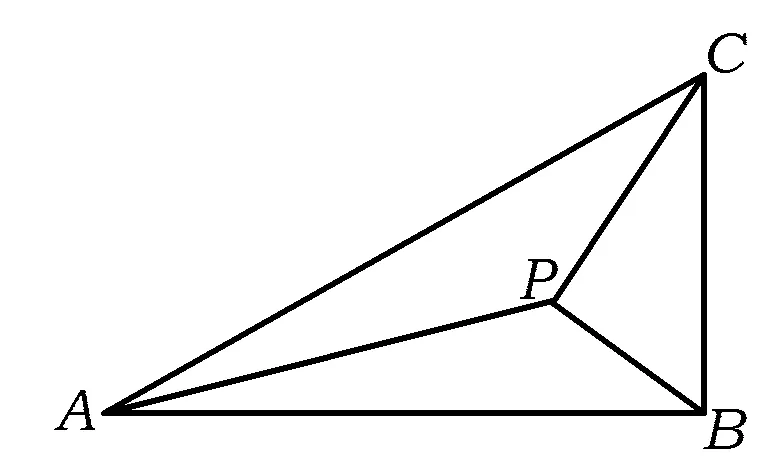
图4

2)若∠APB=150°，求tan∠PBA.

(2013年全国数学高考新课标卷Ⅰ理科试题第17题)

分析1)略；

2)设∠PBA=θ，则∠PCB=θ，在△PAB中，

在△PCB中，

设计意图例2的△BCD中已知两个量BC,BD，从相邻的△ABD(已知3个量)中得到第3个量∠BDC的值.变式与例题方法完全类似，只是所求量AD·sin∠BAD在一定程度上有陌生感，可以分开处理，也可以过点D作AB的垂线，构建所对应的几何线段.例2及变式中所需的第3个量均可以从相邻的三角形中获得，但拓展中的第2)小题，发现无法从外界获得第3个量(因为外界相关的三角形中均只有两个量).仔细研究发现：若引入第3个量，则可确定所需三角形及相关三角形，于是大胆、自主引入第3个量，求解第4个量，用方程的思想来解决问题.

3)已知两个量，求取值范围.

变式1设△ABC内角A，B，C的对边分别为a，b，c，已知a=bcosC+csinB.

1)求角B；

2)若b=2，求△ABC面积的最大值．

(2013年全国数学高考新课标卷Ⅱ理科试题第17题)

(2011年全国数学高考新课标卷Ⅰ理科试题第16题)

1)求角B的大小；

2)若a+b=1，求b的取值范围．

(2013年江西省数学高考理科试题第17题)

案例2“空间几何体”的体积、表面积

求“空间几何体”的体积及表面积，实质是要明确空间几何体的结构特征，并能进一步度量和计算长度、表面积、体积等.几何体结构特征的复杂程度、陌生程度有效地考查了空间想象能力，依此构建3层目标，并分层落实：1)单一的简单几何体，以三视图为载体进行考查，并对几何体作切、挖、转等处理；2)简单几何体的组合，并可作一定的开放性探索；3)与球体有关的组合型几何体,主要考查球的截面的几何性质、几何体的外接球半径等.具体论述如下：

1)单一的简单几何体.

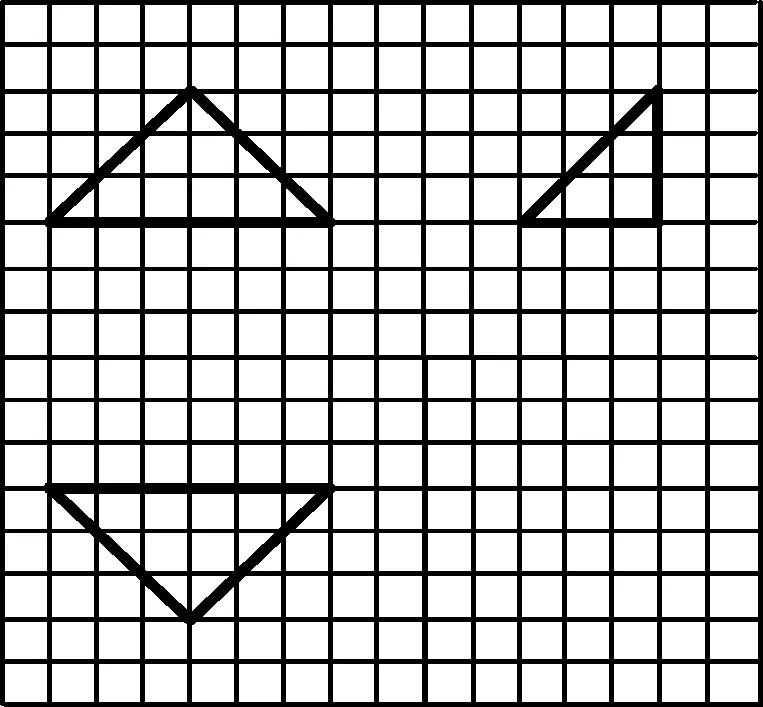
图5

例4如图5，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为

( )

A．6 B．9

C．12 D．18

(2012年全国数学高考新课标卷Ⅰ理科试题第7题)

变式1一个四面体的顶点在空间直角坐标系O-xyz中的坐标分别是(1,0,1)，(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时，以zOx平面为投影面，则得到的正视图可以为

( )

A. B. C. D.

(2013年全国数学高考新课标卷Ⅱ理科试题第7题)

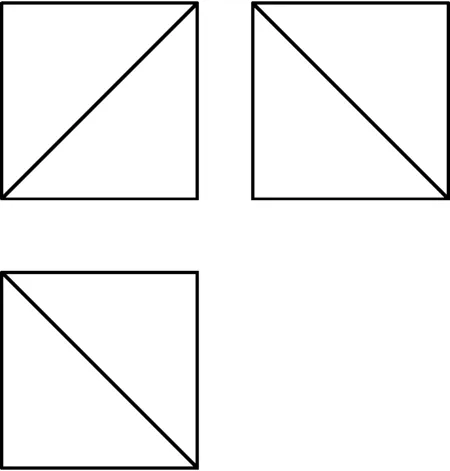
图6

变式2一个正方体被一个平面截去一部分后，剩余部分的三视图如图6所示，则截去部分体积与剩余部分体积的比值为

( )

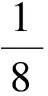
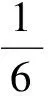
(2015年全国数学高考新课标卷Ⅱ理科试题第6题)

( )

A.17π B.18π C.20π D.28π

(2016年全国数学高考卷Ⅰ理科试题第6题)

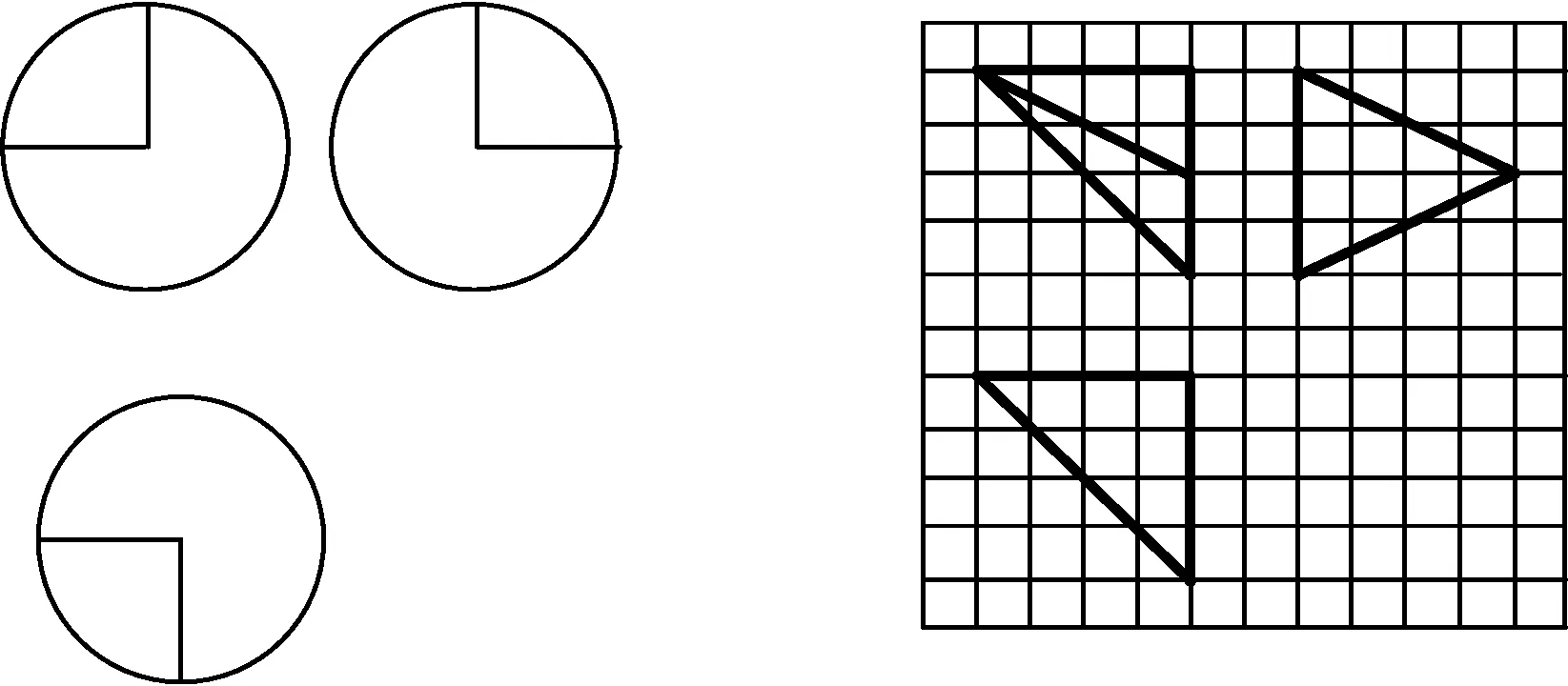
图7 图8

变式4如图8，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为

( )

(2014年全国数学高考新课标卷Ⅰ理科试题第12题)

分析变式4有两种解法：一是正方体切割；二是几何体旋转.

方法1用正方体进行切割，作线太多，易乱.按三视图依序简化图形处理，具体如图9所示.

图9

方法2几何体的旋转，可以带来三视图的旋转及视图位置的改变，把不熟悉的三视图转化成熟悉的三视图结构，容易还原几何体.此题中，保持几何体的正视方向不变，把几何体沿顺时针方向旋转90°，侧视与俯视交换位置.具体如图10所示.

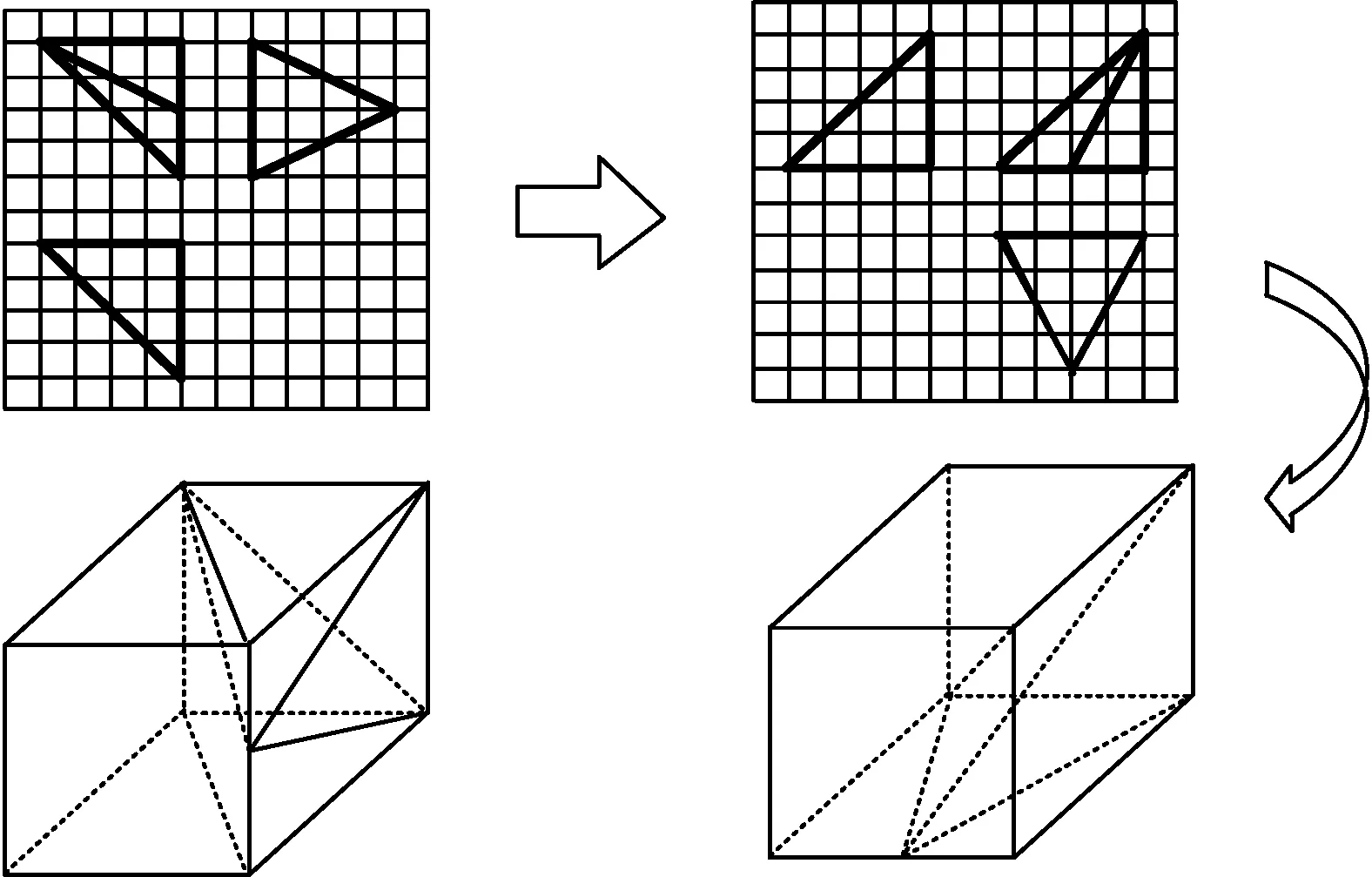
图10

( )

A.14斛 B.22斛 C.36斛 D.66斛

(2015年全国数学高考新课标卷Ⅰ理科试题第6题)

设计意图此类问题的考查主要是以三视图为载体来进行，可以逆向考查(变式1)；也可以对简单几何体用平面截(变式2)；挖去一部分(变式3、变式4)，甚至可以把简单几何体转动一个角度(变式4)，其中变式4是一个难点，要多角度给以突破.拓展1则把空间几何体与数学文化(数学史知识及数学应用)作了一个很好地融合.

2)简单几何体的组合.

例5某几何体的三视图如图11所示，则该几何体的体积为

( )

A．16+8π B．8+8π

C．16+16π D．8+16π

(2013年全国数学高考理科试题第8题)

图11 图12

变式1圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体，该几何体三视图中的正视图和俯视图如图12所示.若该几何体的表面积为16 + 20π，则r=

( )

A.1 B.2 C.4 D.8

图13

(2015年全国数学高考新课标卷Ⅰ理科试题第11题)

拓展1在一个几何体的三视图中，正视图和俯视图如图13所示，则相应的侧视图可以为

( )

A. B. C. D.

(2011年全国数学高考新课标卷Ⅰ理科试题第6题)

设计意图例5与例4的考查方向、载体都相同，但会把多个“残缺式”简单几何体进行组合(拼接或消融)处理，要加强对表面积、侧面积等概念的理解；拓展1从正视图、俯视图能大概推断几何体的形状，从而得出侧视图，虽不能确定，但选项可选，有一定的开放性.

3)与球有关的几何体.

与球有关的几何体主要考查两个方面：球的几何性质(球心与截面圆心的连线垂直于截面)及几何体的外接球.紧扣球的两个要素：球心、半径.

(2011年全国数学高考新课标卷Ⅰ理科试题第15题)

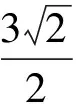
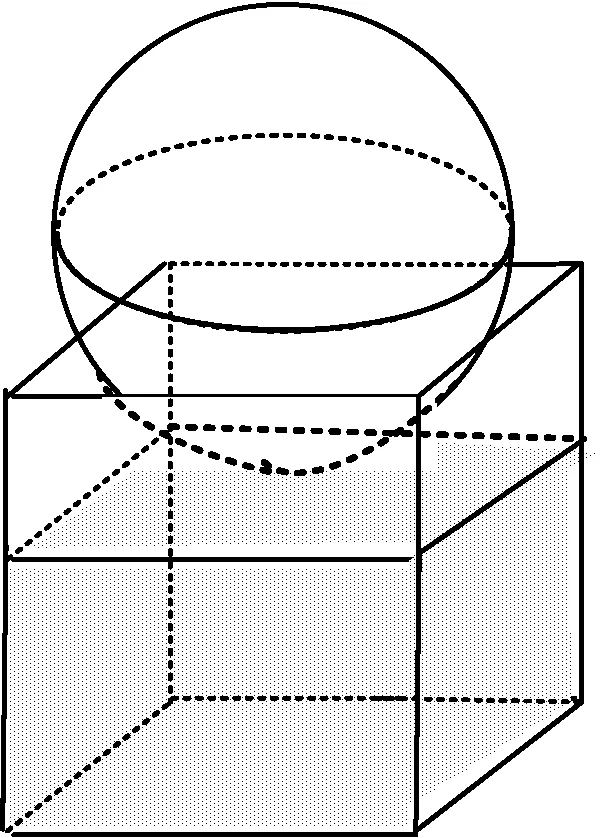
图14

(2013年全国数学高考新课标卷Ⅱ文科试题第15题)

变式2如图14，有一个水平放置的透明无盖的正方体容器，容器高8 cm，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6 cm，如果不计容器的厚度，则球的体积为

( )

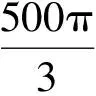
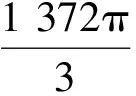
(2013年全国数学高考新课标卷Ⅰ理科第6题)

拓展1已知三棱锥S-ABC的所有顶点都在球O的球面上，△ABC是边长为1的正三角形，SC为球O的直径，且SC=2,则此棱锥的体积为

( )

(2012年全国数学高考新课标卷Ⅰ理科第11题)

分析若要把球画出来，则作图会存在困难.一个好的策略是跳出球来画几何体，标出球心及半径就好.具体思维过程如图15所示.

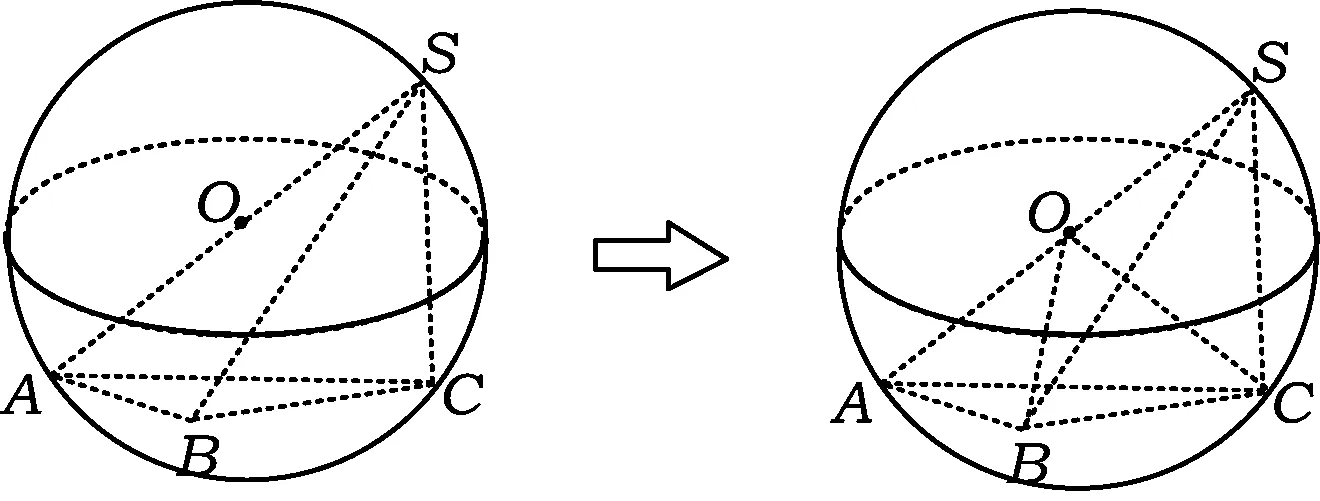
图15

易得VS-ABC=2VO-ABC=

类比拓展1，尝试对例6改编，可得：

分析如图16，易得VS-ABCD=2VO-ABCD.

图16

设计意图例6及变式1、变式2通过构建球心与截面图形构成的几何体为载体，加强对这一几何性质的考查；拓展1则把这类几何体的顶点由球心拓展到了球面，若没有看透本质，则问题识别会有困难，形成解题障碍.

分析以下3种解法的思维过程如图17所示：

图17

解法1补形成长方体，易知四面体的外接球即长方体的外接球.

解法2翻折图形的对称性，过△ACD的外心O1作垂线l1，同时过△ABD的外心O2作垂线l2,且l1∩l2=O,易得点O到点A，B，C，D的距离相等，即点O为外接球心.

解法3先找外心再定球心，属常规解法.过△ACD的外心O1作垂线l1，则球心O必在l1上，只要OB=OD即可.

变式1设三棱柱的侧棱垂直于底面，所有棱长都为a，顶点都在一个球面上，则该球的表面积为

( )

(2010年全国数学高考新课标卷Ⅰ理科试题第10题)

(2016年江西省南昌市第二次模拟考试试题)

拓展1四面体ABCD的一条棱长为x，其余棱长为3，记四面体ABCD的体积为F(x)，则函数F(x)的单调增区间是______，最大值为______；当该四面体体积最大时，经过这个四面体所有顶点的球的表面积______.

(2015年北京市西城区第一次模拟考试理科试题第14题)

设计意图例7的选取很重要，该几何体不同的结构特征对应多种不同的思维方式.如该几何体可以补形成长方体，转化成长方体的外接球来求；可以根据翻折几何图形的对称性直接找到球心；还可以用先找外心再定球心的方式来算出半径.变式1～3对这几种方法作了一定的巩固、提升，其中变式1是解法1的基础巩固与本质提炼，变式2用解法1和解法3都可以解决，变式3是解法2的巩固和提升.拓展1实质上是对变式3的二面角A-BD-C做了一个动态处理(体积最大，意味着该二面角为直二面角)，加大了思维量.

4 思考感悟

例题、变式及拓展的设计，决定因素在于教师.教师要跳进题海，追本溯源，总结问题的变式及拓展，并加深对问题本质的认识，重构更完善的知识网络结构.

例题、变式及拓展的设计，目标意识是关键，其次要有小单元整体设计思路.这样才能够引导学生自觉进入深度学习，提升数学核心素养.

当然，这些都要结合学情去思考才有价值，才能让学生的基础、能力得到同步提升，提高解题能力，提升备考效果.

[1] 李慧娟,傅海伦,权奎.数学学习的碎片化与整体化[J]．中学数学杂志，2016(11)：7-9．

[2] 教育部考试中心.2017年普通高等学校招生全国统一考试大纲的说明(理科)[M]．北京：高等教育出版社,2016．

[3] 李伟.全国卷形势下数学备考的策略[J].课程教学研究,2015(12):60-63.

2017-02-20；

2017-03-21

李 伟(1976-)，男，江西临川人，中学高级教师.研究方向：数学教育.

O123.1

：A

：1003-6407(2017)07-13-05