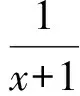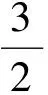一题一惑 一探一获
——利用曲线的公切线研究函数不等式
●
(单县第一中学 山东单县 274300)
一题一惑一探一获
——利用曲线的公切线研究函数不等式
●卫小国
(单县第一中学 山东单县 274300)
将函数不等式的求参与证明问题,利用分离函数的方法,转化为两条曲线的公切线进行解答.文章给出一种新的解题思路,在减少运算的同时,培养学生数形结合与转化化归思想的灵活运用.
不等式;公切线;数形结合
含参函数不等式问题,因其是考查学生问题转化能力、数学运算能力和创新解题意识的好载体,而成为各地考试命题的热点.笔者结合一次教学中学生对所提供解法的释疑,提出一种利用曲线的公切线解函数不等式的方法,与大家共研.
例1已知函数f(x)=ax2-lnx(其中a>0)有两个不同的零点,求a的取值范围.
学生在课堂上提供了两种解法,解题切入点不同,但都属于常规方法.
1 一题多解
解法1求得导函数
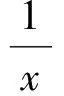
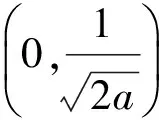
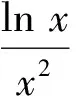
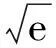
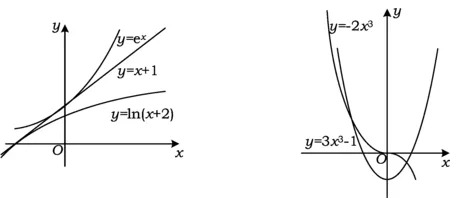
故

评注解法1从导数的应用入手,结合函数的单调性、极值与最值,研究函数的性态,掌控解题的关键(函数的最小值决定零点的个数),整个解题过程自然[1];解法2借助辅助函数g(x)的零点,是典型的数形结合思想,相比解法1似乎更巧妙,但本质上与解法1异曲同工.
2 一解有惑
有学生也获得正确的结论,但是给出了不同的解答,过程如下:

图1
设g(x)=ax2,h(x)=lnx,可知两个函数图像只有1个公共点.设该公共点为(x0,y0),则满足
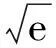
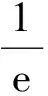

图2 图3
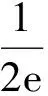
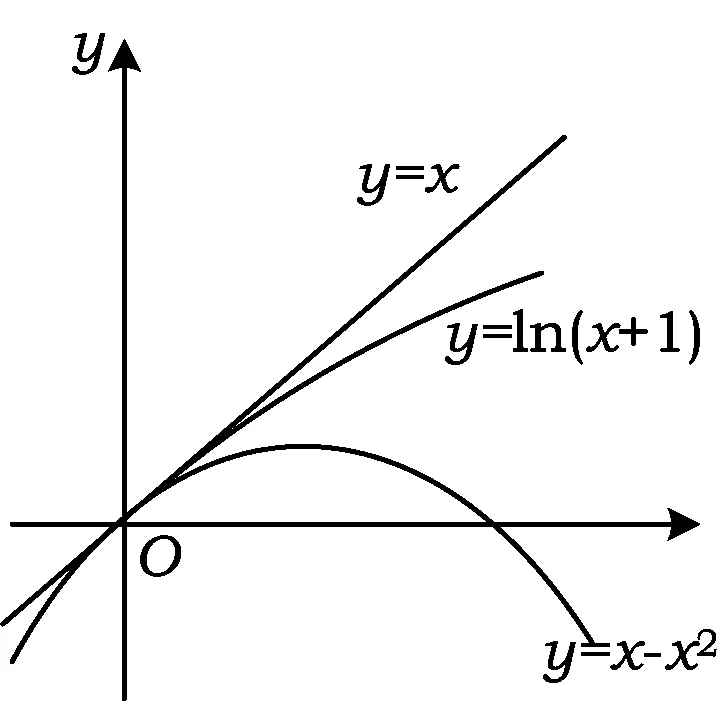
笔者针对这种“公切线分隔法”,提炼出一般解题思路为:证明或求解f(x) 笔者运用“公切线分隔法”研究近几年数学高考试题中的类似问题,发现此类问题可进一步分为“公切线共切点”和“不共切点”两种情况,或者曲线分别处于切线同侧和异侧两种位置关系.近几年考查此类问题的高考题有:2013年全国数学高考新课标卷Ⅱ理科第21题、2014年辽宁省数学高考理科第11题、2014年全国数学高考新课标卷Ⅰ理科第11题、2015年山东省数学高考理科第21题第2)小题.笔者以前两道高考试题为例,简单阐述不共点同侧与共点同侧这两类题型的解法. 例2已知函数f(x)=ex-ln(x+m),当m≤2时,证明:f(x)>0. (2013年全国数学高考新课标卷Ⅱ理科试题第21题) 分析当m≤2时, f(x)=ex-ln(x+m)≥ex-ln(x+2), 只需证 ex-ln(x+2)>0. 易知y=ex与y=ln(x+2)的图像没有公共点,如图4,结合函数不等式知ex≥x+1(其中y=ex与y=x+1仅相切于点(0,1),且除公共点外,前者在后者的上方).另外,函数不等式x+1≥ln(x+2)类似的几何特征为:y=ln(x+2)与y=x+1仅相切于点(-1,0),此外前者在后者的下方.即y=ex与y=ln(x+2)分别处于公切线y=x+1的两侧,由图4知f(x)>0显然成立. 图4 图5 例3已知函数f(x)=ax3-3x2+1,若f(x)存在唯一的零点x0,且x0>0,则a的取值范围为 ( ) A.(2,+∞) B.(1,+∞) C.(-∞,-2) D.(-∞,-1) (2014年全国数学高考新课标卷Ⅰ理科试题第11题) x1=-1,a=-2, 进而求得公切线为6x+y+4=0.当a=-2时, F(x)=g(x)-h(x)=-2x3-3x2+1= (1-2x)(x+1)2, 评注将不等式转化、设计成两个函数的不等关系;辅以简图分析,直观呈现对应曲线间的位置,为数形结合解决不等式问题提供依据.选取特殊情形(曲线的相切)为突破,巧妙获取参数的范围,并推理论证,使得该不等式求参问题获得合理解决.从以上试题的解答中,可见关键是将不等式拆分为两个常规的基本函数的不等关系.从函数图像上易于发现两者位置上的关系,进而确定化归的可能与类型;辅以数形分析,会使得解答相对简捷[3]. 以上例题中在切点附近,其中一条曲线始终在另一曲线的上方,而2015年山东省数学高考理科第21题的第2)小题却略有不同. 例4设函数f(x)=ln(x+1)+a(x2-x),其中a∈R. 1)略. 2)若对任意x>0,f(x)≥0成立,求a的取值范围. (2015年山东省数学高考理科试题第21题) 图6 分析令g(x)=ln(x+1),h(x)=-a(x2-x),如图6,当a≥0时才有 ln(x+1)+a(x2-x)>0. 易知g(x)与h(x)相交于点(0,0),由g′(0)=1,h′(0)=a知g(x)与h(x)存在共点的公切线,此时a=1且公切线为y+x=0. 当a=1时, F(x)=g(x)-h(x)=ln(x+1)+x2-x, 当x>0时,F′(x)>0,则F(x)在(0,+∞)上单调递增,即F(x)>F(0)=0恒成立. 综上所述,当a=1时,在y轴的右侧两条曲线的位置关系为:g(x)的图像恒在h(x)的上方.由图6知a<1也满足,故a∈[0,1]. 将复杂的不等式问题简化为函数的大小问题,水到渠成地运用数形结合思想,将其化归为曲线位置关系的研究.解题过程简洁,运算难度降低,解法略显简捷,以特殊化解决问题,展示了较高的创新意识和辨析能力. 有兴趣的读者,可继续研究下面两道高考试题: 例5当x∈[-2,1]时,不等式ax3-x2+4x+3≥0恒成立,则实数a的取值范围是 ( ) C.[-6,-2] D.[-4,-3] (2014年辽宁省数学高考理科试题第11题) (2010年天津市数学高考文科试题第20题) 反思导数解不等式问题的基本方法是构造函数模型,如何构造、怎样运算、何时分类讨论都是难点.通过此类题可以考查学生的综合数学素养,因此参考答案更多的是构造函数解决,利用导数与单调性知识求最值.若考生熟练掌握常见曲线的几何特征,则能“以形助数,以数解形”,运用直观的方式呈现不等关系,从而在模式化的解法基础之上,又提供了一种新的思路.如此是试题的巧解还是解答的巧合,亦或是命题人的有心,值得品味! [1] 霍福策,曹军.转化与化归在不等式恒成立中的应用[J].数学教学研究.2014(1):45-48. [2] 李金兴,许兴铭.函数与导数专题[J].中学教研(数学),2017(2):33-38. [3] 陈晓明.问题到底出在哪儿呢——对一道导数试题解法的探究[J].数学教学,2017(1):12-13. 2017-02-25; 2017-03-26 卫小国(1979-),男,湖北武汉人,中学一级教师.研究方向:数学教育. O123.1 :A :1003-6407(2017)07-21-033 一探有获
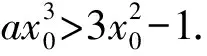
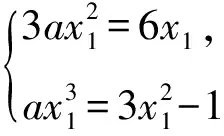
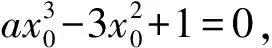
4 解后有疑